观测误差对非线性环境模型参数识别的影响
文章编号:025322468(2003) 0620781205 中图分类号:X32 文献标识码:A
杜鹏飞,邓义祥1 ,陈吉宁 (清华大学环境科学与工程系,北京 100084)
摘要:采用SCE-UA 方法和RSA 方法,比较了在不同的观测误差条件下,优化方法和不确定性分析方法对于非线性模型参数识别的影响. 分析表明,RSA 方法是在具有观测误差的数据条件下进行参数识别的一种有效手段. 同时,通过比较分析,发现RSA 方法预测的浓度平均值和概率最大值与“真实值”并不完全一致. 因此,在使用RSA 方法时,应该充分考虑预测区间,以降低决策风险.
关键词:观测误差;不确定性分析;SCE-UA;RSA
Effects of observation errors on parameter identif ication of a nonlinear environmental model
DU Pengfei ,DENG Yixiang ,CHEN Jining(Department of Environmental Sciences and Engineering Tsinghua University ,Beijing 100084)
Abstract :Parameter identification is a crucial procedure for model application. Observation errors are widely present in environmental data. Thispaper focused on the effects of observation errors on parameter identification of nonlinear environmental models. It specifically compared the identification results by the optimization and uncertainty analysis approaches , taking the SCE-UA and RSA methods as representatives respectively. It was found that the RSA was an effective approach to reduce the impacts of observation errors. It was also showed that the idntified average values or the statistically most likely values of the RSA were often not in consistence with the“true values”. It is there fore suggested that the intervals be considered as identified parameter uncertainty so as to reduce the decision2making risks.
Keywords :observation errors ; uncertainty analysis ; environmental model ; SCE-UA; RSA
作者简介:杜鹏飞(1970 —) ,男,副教授E2mail :dupf @tsinghua. edu. cn
数学模型是环境规划与管理的重要手段,参数是数学模型必不可少的组成部分. 一般情况下,数学模型的参数必须通过识别加以确定. 因此,参数识别是数学模型应用的重要步骤. 然而,由于环境系统的复杂性和环境监测条件的相对滞后,人们可以获得的数据往往十分有限,并且不可避免地存在着观测误差,给数学模型的参数识别带来了严重的影响.
优化方法是传统的参数识别技术,在环境领域以及其它领域都有比较广泛的应用. 优化技术的研究成果不断涌现,由Duan 等人提出的SCE-UA 方法是比较公认的具有较高效率的优化方法之一. RSA 方法是由Hornberger 和Spear 等人提出,它是基于随机采样的不确定性分析方法. 本文将采用上述2 种方法研究观测误差对非线性环境模型参数识别的影响.
1 模型描述
考虑一个简单的子过程方程,即污染物衰减模型:
d C/d t = - k′C (1)
式中, C 为污染物的浓度(mg/L) , k′为衰减系数(1/d) , t 为时间(d) .
这里假设k′不是常数,而与污染物浓度有关:
k′= kC/( C + M) (2)
式中, k 是系数(1/d) ,M 是限制因子(mg/L) .
根据式(2) ,当C m M 时, k′近似为常数;当C n M 时,则k′近似与C 成正比.
联立(1) (2) 两式: d C/d t = - kC2/( C + M) (3)
积分可得: - ln C + M/C = kt - ln C0 + M/C0 (4)
其中, C0 为初始时刻污染物的浓度(mg/L) .
注意到式(4) 中C 是t 的单调函数,因此在k 、M 和C0 已知的情况下, C 是可唯一确定的.因此记C 为t 的函数:
C = C( C0 , k ,M , t) (5)
选择该模型作为研究对象,主要考虑到以下几个方面的因素:首先,它是许多环境模型的组成部分,在实际中有广泛的应用;其次,模型是动态和非线性的,参数之间具有较强的相互作用;最后,模型的结构比较简单,参数之间的关系容易把握.
2 数据序列的产生
本文采用合成的“观测”数据进行研究,即在已知参数值的情况下采用式(4) ,产生“真实值”时间序列,然后加上随机挠动以模拟观测误差,得到“观测值”时间序列,然后利用这些数据进行模型的识别和验证. 这样做的目的,是为了使系统的真实情况在掌握之中,同时模型没有结构上的误差,参数估计的所有的误差仅来源于初值和观测系列. 这使得有可能在排除结构误差的情况下,单独研究观测误差对于参数识别的影响. 合成数据方法在许多模型分析中有广泛的使用[1 ] . 为简洁起见,在不引起混淆的情况下,不再对“观测值”和“真实值”加上引号.
令C0 = 20 mg/L , k = 0.2/d ,M = 10 mg/L ,由于方程(4) 是一个非线性方程,因此对于给定的时刻t ,采用牛顿方法解非线性方程求出C 值[2 ] ,再加上均值为0、标准方差为1 m/g 的随机挠动,即挠动项为: ξ~ N (0 ,1) (6)
观测值C′为: C′(t) = C( t) + ξ (7)
显然,观测误差满足独立、正态和同方差的性质.
3 目标函数
由于具有多个时刻的采样值,因此必须将多目标转化为单目标. 考虑到上述观测误差是正态的独立同分布,此时最大似然方法与最小二乘法是等价的,即目标函数为模拟值与实测值差的平方和. 大量的经验表明,如果观测误差满足上述关系,则最小二乘法目标函数是最优的目标函数. 由于模型没有结构误差,本文不再对方法进行相关性分析.
由于C0 的特殊性,这里考虑将C0 作为参数和不作为参数2 种方案. 不识别C0 时,参数取值空间为Ω = { ( k ,M) | 0 ≤k ≤2 ,0 ≤M ≤100} ;识别C0 时,参数取值空间为Ω = { ( k , M ,C0 ) | 0 ≤k ≤2 ,0 ≤M ≤100 ,15 ≤C0 ≤30}.
4 优化方法的识别与分析
4.1 SCE-UA 方法
优化方法是传统的参数识别技术之一,它的形式很多,收敛速度各有不同,但本质是一样的[3 ,4 ] . 本文采用SCE-UA 优化方法.
SCE方法是Duan 等人于1992 年在吸收了控制随机搜索方法和遗传算法的基础上提出 的[5 ] ,1993 年对其进行了修正,称为SCE-UA 方法[6 ,7 ] . SCE-UA 方法在水文学模型中得到了广泛应用,是到目前为止对于非线性复杂模型采用随机搜索方法寻找最优值最为成功的方法之一[5 —8 ] . SCE 方法的主要步骤为:
步骤0 初始化. 选择p ≥1 和m ≥n + 1 ,这里p 是复杂形的个数, m 是每一个复杂形的点数,计算样本数s = p ×m.
步骤1 产生样本. 在可行空间Ω< Rn 采取s 个点x1 、x2 、.、xs . 计算在点xi 处的函数值f i . 在缺少前验信息的条件下,采用均匀采样分布.
步骤2 对点进行排序. 将s 个点以升序进行排列,将它们存贮到数组中: D = { xi , f i , i =1 , ., s} ,因此i = 1 代表了目标最小的函数点.
步骤3 复杂形划分. 将D 划分为p 个复杂形A1 , .,Ap ,每一个包括m 个点,以使:
![]()
步骤4 根据竞争复杂形演化算法对每一个复杂形进行演化.
步骤5 混合复杂形. 将A1 , .,Ap 替代到D 中,以使D = { Ak , k = 1 , ., p} ,对D 按目标函数的升序进行排列.
步骤6 检查收敛性. 如果满足收敛的标准,则结束搜索,否则回到步骤3.
有关SCE-UE 方法更为详细的介绍见参考文献.
4.2 初值不作为参数
采用真实序列进行参数识别,识别的结果为k = 0120 ,M = 9198 ,基本上等于模型的真实参数,说明在没有观测误差的条件下,SCE-UA 方法能够有效的识别系统的真值. 但如果采用观测值序列,则识别的结果分别为k = 1 , M = 8116 ,尽管模拟的结果尚可,最大相对误差不超过10 %(见图1 (a) ) ,但参数识别结果与真实值的误差高达400 %和716 %.
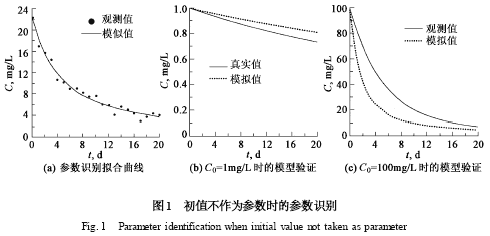
采用C0 = 1 mg/L 和100 mg/L 的系统状态进行模型验证,则最大相对误差分别为1016 %和5418 % ,见图1 (b) 和图1 (c) . 可见,当模型进行外推时,误差将显著增大.
4.3 初值作为参数
当k 和M 确定以后,只要C0 确定,模拟时间序列就唯一确定了. 因此, C0 既是观测值,也具有参数的特点. 因此可将初值也作为未知参数进行识别. 采用SCE-UA 方法进行搜索,3 个参数的识别结果分别为: k = 0126 ,M = 1511 , C0 = 2011 ,误差分别为3015 %、5017 %和0125 %. 最优参数的拟合曲线与观测的对比见图2 (a) .
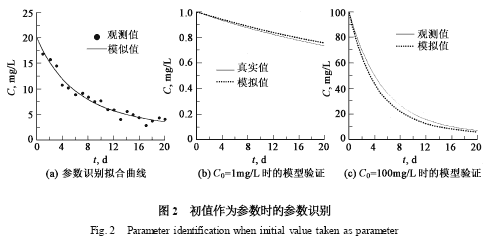
将k 和M 的识别结果代入到C0 = 1 mg/L 和100 mg/L 进行模型验证,见图2 (b) 和图2 (c) .与不将初值作为参数进行识别相比,模型识别精度的改进非常明显. 对C0 = 1 mg/L 和100 mg/L的系统状态进行检验,则最大相对误差分别为3110 %和19192 %.
5 RSA 方法的识别与分析
5.1 RSA 方法
20 世纪70 年代末、80 年代初,由于认识到模型识别的困难,Hornberger 和Spear 将过于强硬的优化条件弱化,即将其转化为一些可以用定量或定性的语言描述的条件来决定参数的取舍,从而在一定程度上克服了采用优化方法进行参数识别而带来的不确定性问题,这就是RSA方法. RSA 方法是基于行为和非行为的二元划分进行参数识别的,换句话说,给定一组参数,如果系统的模拟行为满足事先设定的条件,那么这组参数就是可接受的,否则是不可接受的. 该方法的主要步骤如下:1.确定参数的初始分布F(θ) . 如果对参数的分布特性没有比较确切的了解,可假设参数在取值区间上均匀分布. 2.根据模拟值和观测值的对比,确定行为参数( B)和非行为参数( NB) 的划分准则. RSA 方法对行为参数的划分准则非常灵活. 这提高了RSA 方法的适用范围. 3.从参数的初始分布随机采样,取得一组参数,带入模型进行模拟. 如果模拟的结果是可以接受的,那么认为这组参数是行为参数,是可以接受的;否则是非行为参数,是不可以接受的. 4.重复步骤2 和3 ,直到取得足够的样本数为止.
在参数空间随机采样1 万次,取对应目标函数最小的5 %参数为可接受参数. 为提高采样的效率,采用Latin Hypercube 方法[9 ,10 ] 替代传统的Monte Carlo 采样.
5.2 识别结果
从4.2 节和4.3 节的讨论可以看出,将初值作为参数能够更好地进行系统识别,因此RSA方法只考虑将初值作为参数的情况.
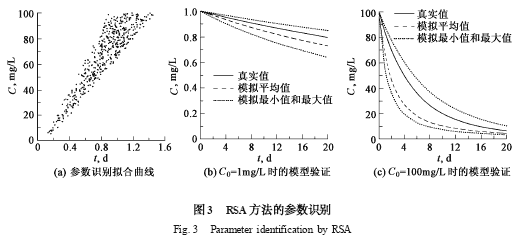
RSA 方法的模型识别结果见图3 (a) . 由于采用了可接受行为的定义,所获得的不再是单一的参数,而是由大量可行参数所组成的集合,其分布具有明显的区域性特点.
当C0 = 1 mg/L 和100 mg/L 时的模型验证见图3 (b) 和图3 (c) . 可以看出,各时刻物质浓度值的预测区间覆盖了真实值,从而使模型能充分地估计预测结果的风险. 但是,与优化方法相比,RSA 方法在一定程度上牺牲了模拟精度以换取可靠性,这体现了在参数识别过程中估计精度和可靠性之间的矛盾,对其仍然需要进一步的研究.
从图3 (b) 和图3 (c) 可看出,RSA 方法预测的浓度平均值与真实值存在一定的偏差. 因此,在应用RSA 方法时,使用均值或概率最大值仍具有潜在的风险,应充分考虑模型预测结果的范围,以降低决策风险.
6 结论
本文采用SCE-UA 方法和RSA 方法,研究了观测误差对模型参数识别和预测的影响. 为避免模型结构误差的影响,引入了合成数据方法. 在具有观测误差的情况下,采用优化方法不能很好地识别模型的参数. 在本例中优化方法的分析表明,将初值作为参数进行识别,可提高系统的可识别性. 采用RSA 方法,参数识别结果不再是单一值,而是由大量可行参数所形成的集合. RSA 在一定程度上克服了观测误差带来的预测风险,但模型预测的精度也因此而降低. 这体现了参数识别时预测精度和可靠性之间的固有矛盾.
参考文献:
[ 1 ] Ratto M,Tarantola S ,Saltelli A. Sensitivity analysis in model calibration :GSA2GLUE approach[J ] . Computer Physics Communication ,2001 ,136 :212 —224
[ 2 ] 徐士良. Fortran 算法常用算法程序集[M] . 北京:清华大学出版社,1995. 123 —125
[ 3 ] 弄文训,谢金星. 现代优化计算方法[M] . 北京:清华大学出版社,2001. 1 —245
[ 4 ] 刘 毅,陈吉宁,杜鹏飞. 环境模型参数优化方法的比较研究[J ] . 环境科学,2002 ,23(2) :1 —6
[ 5 ] Qingyun Duan ,Soroosh Sorooshian ,Vijai Gupta. Effective and efficient global optimization for conceptual rainfall2runoff models[J ] .Wat Res Res ,1992 ,28 (4) :1015 —1031
[ 6 ] Soroosh Sorooshian ,Qingyun Duan ,Vijai Kumar Gupta. Calibration of rainfall2runoff models :application of global optimization to the sacramento soil moisture accounting model [J ] .Wat Res Res ,1993 ,29 (4) :1185 —1197
[ 7 ] Duan D Y,Gupta V K,Sorooshian S. Shuffled comples evolution approach for effective and efficient global minimization[J ] . Journal of Optimization Theory and Applications ,1993 ,76 (3) :501 —520
[ 8 ] Qingyun Duan ,Soroosh Sorooshian ,Vijai K Gupta. Optimal use of the SCE-UA global optimization method for calibration watershed model [J ] . Journal of Hydrology ,1994 ,158 :265 —284
[ 9 ] Jining Chen. Modeling and control of the activated sludge process :towards a systematic framework[D] . The University of London , 1993. 130 —165
[10 ] 邓义祥,陈吉宁,杜鹏飞. HSY算法在水质模型参数识别中的应用[J ] . 上海环境科学,2002 ,21(8) :497 —500
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 [email protected] ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








