竖向荷载下柔性接口管道的纵向力学计算

吴为义¹，张土乔¹，郑旭晨²，孙宇坤³
（1.浙江大学市政工程研究所，浙江杭州 310027；2.杭州市市政工程集团公司，浙江杭州 310014；
3.浙江工业大学职教学院，浙江杭州 310014）

　　摘　要：探讨了柔性接口管道在竖向荷载作用下的竖向位移计算方法和计算模型，据此对管道的竖向位移、转角、弯矩、剪力等纵向力学性状进行了计算。通过与工程测试结果比较，验证了该计算方法与计算模型的合理性，为给排水管道的合理优化设计、施工及运行管理等提供了一定的理论基础。
　　关键词：柔性接口管道；竖向位移；纵向力学计算；工程测试
　　中图分类号：TU991.3
　　文献标识码：C
　　文章编号：1000-4602(2002)09-0058-03

　　地下管线的运行故障有些是由管线纵向受力所致，但目前的管道力学计算很少考虑管线的纵向力学性状，且现有的纵向计算也仅将管线简化成简支梁^［1］或多跨连续梁^［2］，与管线实际受力有较大的出入，因而不能准确地模拟管线的实际受力情况。

1 纵向力学计算

1.1 竖向位移计算模型
　　柔性接口管道的接口允许相连管段间有一定程度的相对转动，它一般不传递弯矩，但能够抵抗一定的张拉、收缩变形，故可认为柔性接口管道系由各管段间通过活动铰连接而成。柔性接口允许管道轴向能够自由伸缩一定距离，且管道中一般不出现因温差而产生的轴向力，因而管段间的轴向力作用可不计。根据弹性假定，管道周围的土壤是有一定抗压刚度系数的弹性体，管顶以上土壤为作用于管道上的主动荷载，而管底以下土壤受压缩并可视为一系列受压的土弹簧，即每节管段均可被视为一根短弹性地基梁。从而，柔性接口管道可模拟为相邻管段通过活动铰连接、受无数土弹簧支撑的若干短弹性地基梁的组合结构,且其与检查井、支墩等边界连接处为固端边界。
　　对于任意第i节管段，假定：
　　①管段底部的土壤为完全弹性土体(符合Winkler弹性假定)；
　　②管段与周围土壤间无相对滑动，即管底以下土壤变形与该管线竖向位移一致(满足变形协调条件)；
　　③同一地区给水、排水管道的埋设深度一般变化不大，从而作用于管段顶部的垂直荷载变化不大，可认为呈均匀分布。
　　管道由n节管段组成，从左到右依次记为第1、2…n节，中间n-1个接口依此记为第1、2…(n-1)个接口，每节管段长度均为L′。第i节(i=1，2，…， n）管段的变形情况见图1。

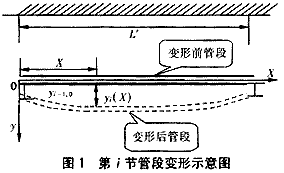
　　由Winkler弹性地基梁理论得出微管段的弯曲微分方程：
?　　　　　EI［d⁴y_i(x)／dx⁴+Kyi(x)］=q₀　　　　(1)
　　式中 ?EI——管段的抗弯刚度
?　　　　　K——管段地基基床换算系数
?　　　　　x——沿管段方向的横坐标，对任意节管段，坐标原点均选在其最左端，x=L′表示其最右端
?　　　　　q₀——作用于管段上的竖向均布荷载，主要包括管顶垂直土压力、竖向附加压力、动荷载、管体自重与介质重量等
　　　　　　yi(x)——第i节管段上x位置处的竖向位移
　　由任一节管段的弯曲微分方程可得每节管段的竖向位移方程，从而可得整条管道的竖向位移曲线。
1.2 模型的求解
　　方程(1)解的一般解析表达式为：?
?　　　　　　yi(x)=e^βx(Ci1cosβx+Ci2sin x)+e^-βx
　　　　　　　(C_i3cosβx+C_i4sinβx)+q0／K　　　　　　　(2)
　　式(2)中的特征系数β=[K／(S／4EI]^4/1，第i节管段的4个待定积分系数C_i1、C_i2、C_i3、C_i4可由每节管段的相应边界条件确定。
　　对于第1节管段，其左端为固端，右端有一定的竖向位移，且弯矩为零，即有
　　　　　　　x=0时，y=0,y′=0?
　　　　　　　x=L′时，y=y1,0，y″=0?
　　对于任意第i(i=2，3，…，n-1)节管段，其边界条件为：
　　　　　　　x=0时，y=yi-1,0，y″=0?
　　　　　　　x=L′时，y=yi,0，y″=0?　　　　(4)
　　对于第n节管段，也有类似式(3)的边界条件：?
　　　　　　　x=0时，y=yn-1,0，y″=0?
　　　　　　　x=L′时，y=0，y′=0?　　　(5)?
　　在上述边界条件(3)、(4)、(5)中，y1,0、y2,0…yn-1，0分别表示第1、2…(n-1)个柔性接口处的竖向位移。?
1.3 纵向力学性状 ?
　　分别对第i节管段（i=1，2，…,n）的竖向位移方程式(2)两边同时求一阶、二阶及三阶导数，再对每个方程式同乘以适当的系数，即可得每节管段的转角、弯矩及剪力等其他纵向力学性状方程。
　　第i节管段上任一点x处的转角为：
?　θ_i(x)=βe^βx［(C_i1+C_i2)cosβx+(C_i2-C_i1)sinβx］-βe^-βx［(C_i3-C_i4)cosβx+(C_i3+C_i4)sinβx］　(6)
　　第i节管段上任一点x处的弯矩为：?
?　Mi(x)=-2EIβ²e^βx(C_i2cosβx-C_i1sinβx)+2EIβ²e^-βx(C_i4cosβx-C_i3）sinβx)　　　(7)
　　第i节管段上任一点x处的剪力为：
　　Q_i(x)=-2EIβ³e^βx［(C_i2-C_i1)cosβx-(C_i1+C_i2)sinβx］-2EIβ³e^-βx［(C_i3+C_i4)cosβx+(C_i4-C_i3)sinβx)］(8)
　　综合式(2)、(6)、(7)、(8)，第i节管段上任一点x处的竖向位移、转角、弯矩、剪力等纵向力学性状可统一表示成矩阵形式：

　　　　

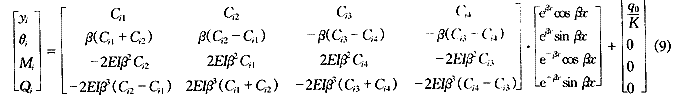
2 工程测试分析

　　笔者对杭州市某大直径预应力钢筋混凝土管的竖向位移进行了长期的现场观测。该管道采用 橡胶圈柔性接口，其一边界端为砖砌井（记为坐标原点），另一边界端为混凝土支墩，两端相距125m，共由25节管段构成（依次记为第1、2、…25节，接口依次记为第1、2…24个接口）。现场测试中布置了1#、2#、3#这3个有代表性的沉降测量点(分别距离原点50、55m、60m)。实测发现，各观测点的沉降量随观测时间的延续由小增大，最后逐渐趋于平缓、稳定，各观测点的最终实测位移（此时距离管道敷设完毕已有一年时间）见表1。

表1 竖向位移最终观测值 观测点 1# ２# ３# 最终沉降量(mm) 38 42 42

　　由管顶土荷载、自重、管内水重等荷载可得作用于管段地基上的附加压力为241.405kPa。根据弹性沉降理论，由L/B、Zi/B（L为基础长度、B为基础宽度、Zi为第i层土深度）值查得各层土的附加压力系数Ci，然后根据公式计算各层土的沉降量，从而得出管道不受边界影响段(距原点55～65m处)的最终沉降量∑ΔS′i=6.614cm。沉降计算经验系数参照规范取为ms=1.0，则管道随基础的最终弹性沉降量为S=m_s∑ΔSi=6.614cm。管道敷设已有一年时间，其时间因数和固结度分别为Tν=Cν·t/H₂=0.4491、U=1-8/π2×e-(π2/4)Tν=0.7323。
　　固结度计算结果说明了管道地基弹性沉降尚未完全，测试结束时已完成的沉降量为Sct=S·U=4.8434cm。由待定参数的确定方法算出管道上每一接口处的转角及竖向位移数值，由于测试管段具有对称性，表2只列出了左半段管段中第i(i=1、2…12)接口处的转角及沉降量计算值。

表2 转角及沉降计算值 转 角(×0.01度) θ₀ θ₁ θ₂ θ₃ θ₄ θ₅ θ₆ θ₇ θ ₈ θ₉ θ₁₀ θ₁₁ θ₁₂ 0.00 1.54 3.08 4.62 6.17 7.71 9.25 7.71 6.17 4.62 3.08 1.54 0.00 沉降值(mm) y_0,0 y_1,0 y_2,0 y_3,0 y_4,0 y_5,0 y_6,0 y_7,0 y_8,0 y_9,0 y_10,0 y_11,0 y_12,0 0.0 1.3 4.0 8.1 13.5 20.2 28.3 35.0 40.4 44.4 47.1 48.4 48.4[

　　管道的实测竖向位移曲线与计算曲线的比较情况如图2所示。

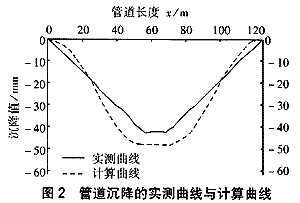
　　由图2可见，实测位移曲线与计算曲线形状基本一致，最大相对误差仅为19.3%。由表2可知，任一个接口处的转角都小于其规范规定的允许转角，说明目前该管道处于安全运行状态，这与管道实际运行情况一致。上述情况证明了管道纵向力学计算模型的合理性与正确性。

3 结语

　　① 敷设于软粘土地基中的管道基础往往不均匀，此时管道受固端等边界约束的影响较大，从而引起管道不同部位处差异性下沉，致使管道纵向受力，严重时会导致管道破裂。
　　② 柔性接口与刚性接口管道的内力传递方式有显著差别，柔性接口管道中的接口处允许相邻管段间有一定的相对转动，一般不传递纵向弯矩，而且接口处能够承受轻微伸缩变形，不会产生由温差引起的轴向力作用。
　　③ 基于管、土之间变形协调原理及一些基本假定，建立了柔性接口管道竖向位移的计算模型，并据此对管道的转角、弯矩、剪力等纵向力学性状进行了计算。该计算方法合理、计算模型正确，能够为管道的合理优化设计、施工及运行管理等提供一定的理论基础。

参考文献：

　　［1］上海市政工程设计院. 给水排水工程结构设计手册［M］.北京：中国建筑工业出版社,1987.
　　［2］邵卫云，张土乔，吴寿荣. 竖向荷载作用下管道形状分析［A］. 城市基础设施发展国际学术研讨会论文集［C］.杭州：浙江大学出版社，1996.

---

　　电　　话：(0571)85597396
　　收稿日期：2002-04-21