给水管网测压点优化布置的模糊聚类法

黄廷林1，丛海兵2
(1.西安建筑科技大学环境与市政工程学院，陕西西安710055；
2.扬州大学环境工程系，江苏扬州225009)

　　摘　要：介绍了测压点优化布置的方法,提出了影响系数的概念,用它表示某一节点水压受其他节点水压波动的影响情况,并采用模糊聚类法对影响系数加以分析。仿真计算结果表明,该方法对于节点流量同步或不同步变化幅度较小的管网测压点优化布置可取得较好的效果。
　　关键词：测压点布置；影响系数；模糊聚类
　　中图分类号：TU991.33
　　文献标识码：C
　　文章编号：1000-4602(2001)11-0050-03

　　水压是给水管网运行质量的重要指标之一。迅速全面地获得管网的水压信息，以便利用计算机进行实时优化调度，以保证供水质量、运行安全、节水节能和运行效率。同时，积累管网实测水压资料可以校验管网微观分析的计算结果，合理进行管网的改造和扩建，永久性测压点正是根据这一要求而设置的。由于测压点必须采用测压装置，故投资大，且过多的测压数据给计算机信息处理带来负担，这就要求选用尽可能少的、具有代表性的测压点安装测压装置，因此其位置的选择也尤为重要。

1　影响系数

　　一个确定的管网，在工作水泵、高位水池高度、节点流量确定的情况下，具有确定的运行工况。但由于外界因素的影响，会引起管网运行工况的变化。运行工况的变化主要表现在节点水压的变化，而最敏感、最频繁的外界变化因素是节点流量。
　　设管网有n个节点，在k节点处产生了ΔQk的节点流量变化值，则全管网节点水压都会受到不同的影响(为ΔH)，其中被考察节点i的水压变化值为ΔHi。k节点自身的水压变化值最大(为ΔHk)，则ΔHi/ΔQk表示k节
点处单位节点流量变化在i节点处产生的水压变化，它反映了i节点水压受其他节点流量变化影响的大小。
　　由于各节点流量基值Qk大小悬殊，绝对值相同的各ΔQk在各Qk中所占的比例不同，因而产生的ΔHi及ΔHk会相差很大。对不同的k节点，ΔHi/ΔQk可比性差。而对ΔQk反映最敏感的是k节点水压变化值ΔHk，且两者变化是同步的，因此选用ΔHi/ΔHk表示k节点流量变化对i节点水压的影响。其物理意义：由于k节点的流量变化,在k节点处产生单位水压变化时，i节点水压的变化值记为Xik=ΔHi/ΔHk。对ΔHi和ΔHk取微分：

　　X_ik=（dH_i）／（dH_k）(i,k=1,2,…,n)　　(1)
　　式中　X_ik——k节点对i节点的影响系数

　　求解Xik可从两方面考虑，一是求解析解,二是直接进行管网微观分析并计算X_ik。k节点的水压变化值，通过各管段的传递影响各管段流量及水泵的工况，进而在i节点产生水压变化，其内在机理复杂，因而求解析解尚不能实现。管网微观分析方法是在某一基准工况下进行管网平差，得出该工况下各节点水压Hi，再加大k的节点流量(其他节点流量不变)重新进行管网平差，得出各节点水压Hi′。其影响系数如下：

　　　　X_ik=（H_i-H_i′）／（H_k-H_k′）(i,k=1,2,…,n)　　(2)
　　式中H_i、H_k——基准工况下i、k节点水压
　　　　H_i′、H_k′——k节点流量改变后i、k节点水压

　　所有X_ik用矩阵表示为［X］_n×n,其主对角线上的元素X_ii=1,其余元素0＜X_ik＜1。

2　模糊聚类及测压点选择

　　模糊聚类^［1］是依据一定的聚类原则和模糊评判标准，将具有相似性质的对象划分为一组。该处被分类的对象是n个节点，聚类原则是比较两两节点的n对影响系数X_ik，将具有相似性质的若干个节点划分为一组。具体步骤如下：
　　①［X］的标准化
　　a.将［X］中各列元素的标准差进行标准化，对k列元素的表达式如下：

　　

　　其余各列算法相同，最后得矩阵［X′］n×n。
　　b.将［X′］_n×n中各列元素的极值进行标准化，对k列元素表达式如下：

　　

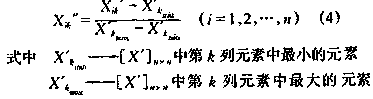
　　其余各列算法相同，最后得矩阵［X″］n×n。
　　②标定
　　标定就是分析［X″］，求出两两节点依X″的相似程度系数rij，从而得到模糊相似矩阵［R］_n×n。
　　由［X″］计算［R］的方法很多，经多次试算比较，最终采用欧氏距离法分析两两节点的模糊关系，其表达式如下：

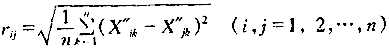　　　　　　　　（5）

　　式中rij——i节点与j节点的欧氏距离
　　　　X″ik、X″jk——［X″］中第i、j行各元素

　　rij反映了i节点与j节点水压波动的相似程度，rij越小说明i节点与j节点越相似。［R］为对称矩阵且主对角线元素为0，其余元素0＜rij＜1。
　　③聚类
　　［R］是［X］的模糊相似矩阵，但不是模糊等价矩阵，现采用从模糊相似矩阵出发的编网法进行聚类。选定某一模糊标准λ∈［0，1］，作［R］的截矩阵［Rλ］，即将［R］≤λ的元素记为1，其余元素记为零；然后在［Rλ］上编网，将n个节点分为若干组。
　　④聚类中心——测压点的确定
　　在上述的每组中选择一个最具代表性的点作为测压点。在一个有m个节点的组别中，每个节点都与其余m-1个节点存在欧氏距离。按照欧氏距离的概念，与其余m-1个节点平均欧氏距离最小的节点是最具代表性的，则选此点为测压点。例如，i节点与其余m-1个节点的平均欧氏距离：

　　　　

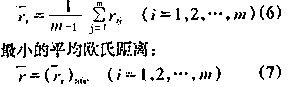
3　算例分析

　　依据上述方法，编制了给水管网测压点优化布置程序，利用该程序对例题进行了仿真计算。该管网由55个节点、94个管段组成。管网的供水点有三个，其中两个为水塔供水,水位分别为78.5、78.1 m，另一个为水泵(一台)供水，其性能曲线为H=86-0.008 89Q²，吸水井水位为3.88 m。
　　计算步骤：首先在基本工况下管网平差得各节点水压Hi，再分别将各节点流量增加某一微量Δq，并分别管网平差得各节点水压Hi′，其余计算如2节中步骤①～④，最后按要求选择每组中的测压点。计算中应注意：λ的选择要综合考虑测压精度和投资两方面因素，以期用较少的测压装置得到较准确的管网压力分布。
　　对该算例进行分析计算的讨论如下：
　　①在基本工况下节点分成10组,测压点分布较均匀，并且在供水分界线附近分布密度较大,其原因是分界线附近节点的水压受分界线两侧水压波动的影响均较显著,其水压波动的节拍与任一侧的节点都不相似，因此它与其余节点的欧氏距离均较大。
　　②改变工况,将节点流量同步变化,变化范围为原工况的0.6～1.4倍，则两两节点的欧氏距离与原工况的相比平均变化了1.6%～4.1%，各组聚类中心与组中节点欧氏距离的均值与原工况的相比变化了0～17.1%。
　　③改变工况,将节点流量不同步变化,即分别将三个水源供水范围内的节点流量减小为原工况的0.8倍。两两节点的欧氏距离与原工况的相比变化了1.8%～2.7%，各组聚类中心与组中节点欧氏距离的均值与原工况的相比变化了0～31.7%。
　　④对于②、③两种情况,若在变化的工况下重新分组,其组数、组中元素及聚类中心与原工况基本相同。
　　⑤在改变后的工况下,利用测压点水压和水源供水量估算各节点水压,对②、③两种情况,估算值与平差计算值相差了0～1.63 m和0～1.59 m。
　　⑥改变水源供水方式,将水塔改为水泵供水，并对②、③两种情况进行计算，结果表明,高位水池供水的水源数越多,聚类性能越稳定。其原因是在计算时水泵未随节点流量的改变进行合理调度，使得各水泵的出水压力随工况变化而剧烈变化,这加剧了节点水压波动的复杂性，在实际管网中这种情况可以避免。

4　结论

　　①根据管网节点水压变化的相关性，运用模糊聚类分析法进行给水管网测压点的优化布置在理论上是合理可行的。
　　②计算结果表明，对于节点流量同步变化或不同步变化幅度较小的管网采用该方法进行测压点优化布置效果良好，具有较好的一致性，对于以重力供水为主的管网尤为适用。

参考文献：

　　［1］王训俭,王增义.论给水管网压力监测点的选择［J］.中国给水排水,1989,5(3):5-12.
　　［2］俞国平.给水管网设计中的一种流量分配方法［J］.中国给水排水,2000,16(4):31-33.
　　［3］赵新华，陈春芳，郑毅.给水管网可靠度的计算［J］.中国给水排水，2000，16(1)：57-60.
　　［4］杨松林.工程模糊论方法及其应用［M］.北京：国防工业出版社，1996.

---

　　电　话：(029)7585478
　　收稿日期：2001-06-28