泵站拍门的诺模计算图
| 论文类型 | 其他 | 发表日期 | 2003-04-01 |
| 来源 | 中国水网 | ||
| 作者 | 张大群 | ||
| 关键词 | 拍门 | ||
| 摘要 | 在大型泵站中采用拍门断流,拍门在停机下落时,其运动过程的计算是相当复杂的。本诺模计算图是在研究拍门下落运动方程并编制拍门优化下落电算程序基础上,为将其计算简化而研制的。使用本诺模图进行拍门设计,不仅可使拍门设计简捷化,而且可以迅速地提供多种方案以资优选。 | ||
张大群(天津市市政工程勘测设计院)
在大型泵站中采用拍门断流,拍门在停机下落时,其运动过程的计算是相当复杂的。本诺模计算图是在研究拍门下落运动方程并编制拍门优化下落电算程序基础上,为将其计算简化而研制的。使用本诺模图进行拍门设计,不仅可使拍门设计简捷化,而且可以迅速地提供多种方案以资优选。
NOMOGRAPHS FOR FLAP GATE USED IN LARGE PUMP-STATION
Zhang Daqun(Tianjin Municipal Engi neeri ng Survey and Desi Institute)
In Iarge pum p-station, the adorption of flap gates to cut off the flow involves the problem of their falling moverment, the calculation of which is a rather complicated matter. This article deals with the equations for falling movement and on the basin of designing programs for optimizing the falling movement a nomograph has been worked out to simplify the work. The result obtained from a nomograph for designing a flap gate is not only simplifies the calculation but also can readily supply alternative plans for use in ophtimization.
一、前 言
拍门是泵站停机时防止因水体倒流引起水泵逆转的一种带有饺链的止逆阀门。安装在流道出口处。
由于拍门的开启角而带来的水头损失,以及停机后拍门下落对门座的撞击力,这两个问题是拍门设计计算的关键。对大、中型泵站尤为重要。
停机后的水泵是经过正转正流、正转逆流、逆转逆的三个阶段。也即停机水泵的过渡过程。各阶段对拍门的作用截然不同。此外,拍门体下落运动中,影响其运动的因素有门重、外拉力、外拉力点、拍门吊点及形心、管道长度及直径、缓冲材料特征及形状等近10种参数。因而对拍门运动过程的计算是相当复杂的。
拍门诺模计算图是将拍门下落运动计算的公式作成计算图表,应用于设计,能将复杂的设计计算简便化。
使用诺模图进行拍门设计,它所提供的数值是近似的。但是,基本上能符合一般的设计要求。同时计算快速、简捷。此外,在设计计算中,经常发生所求的数据不能适应技术设计的特定条件,这就必须反复修正各个已知数据,使所求的数据趋于合理。这项工作利用诺模图将是方便的。借助于诺模计算图能够迅速地提供几种方案,通过数据对比,可选出其中较优的方案。
本文所提出的诺模计算图,适用于带有平衡重或不带平衡重的整体型拍门。它能够计算出拍门开启角度值、外施拉力(平衡重)值、正流阶段时间值,下落角速度值等。本课题曾得到朱肇源、高复栋同志的指导和帮助。
二、诺模计算圈
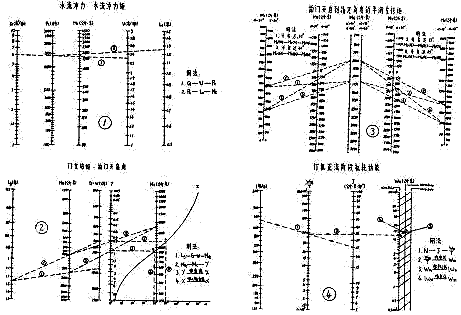
三、用法说明
1.一般说明
(1)按各图所标"用法"的顺序依次计算。
(2)用法中“Q-U-Pc”表示在前面两项所标示的坐标,即Q、U坐标上找出已知的Q及U数值。再联线交Pc坐标上之点,即为所求。如须进一步计算,则用所求出的Pc坐标上之交点为已知点,依次类推求解。
(3)用法中“Y作垂线 X”表示过Y标上已知点作对Y的垂线,交X坐标即为所求。
(4)用法中“X 作平行线 Y”表示过X坐标上已知点,与图中所标出的斜线,(寻求与己知点距离最近处的斜线作平行线)交Y坐标上的点,即为所求。此处X、Y系泛指。
(5)用法中“X作![]() 轴垂线α”表示过X座标上已知点,作向α座标的垂线,交α座标的点,即为所求。
轴垂线α”表示过X座标上已知点,作向α座标的垂线,交α座标的点,即为所求。
2.符号说明
计算图①:
Q——水泵出水流量;
U——出水流道的出口处流速;
Pc——出水水流冲力值;
Lc——水流冲力合力距拍门上饺距离;
Mc——水流冲力矩
计算图②:
G-W——拍门门重与浮力的差值,即浮重
Lg--拍门体重心距拍门上饺距离;
MG——门体浮重转矩;
MC——水流冲力矩;(取图①结果)
y、x——中间参量值;
α——拍门开启角度值
计算图③:
McMG——取图①、图②结果;
MF——平衡重对拍门上铰转矩值;
计算图④:
N——停机前机组的转数;
J——电机与水泵的转动惯量和;
Wm/T——中间参量值;
Wm——停机至流量为零时,机组所消耗的动能;
ω=i·ωH——停机后流量为零的泵转速ω等于额定转速ωH的倍;i一般取0.5~0.7
计算图⑤
L——出水管道中心线长度值;
S——出水管道平均面积值;
T——即L/S值,为中间参量值;
Q——水泵停机前出水流量;
Wf——停机至流量为零时,管道所消耗动能
计算图⑥:
H——停机前水泵扬程值;
Q——流量值;同图⑤
T——即H·Q值、为中间参量值;
Wm+Wf——即图④Wm、图⑤Wf之和;
TB——正流阶段的时间l值;
η——机组的效率
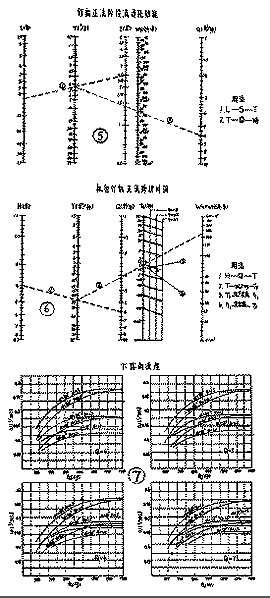
计算图⑦:
Go——不带平衡重时的门重或带平衡重时门重与等效门重(由平衡重转化而来)的差值;
ω——拍门正流结束时的角速度值
3.开启角的计算说明
按计算图①求出水流冲力MC值,按②求出门重转矩MG值,再用Mc、MG依次求出Y、X、α值。α值即为开启角度值。
4.平衡重的计算说明
当门体过重或水流冲力较小,使得拍门正常工作时的开启角小于50°,此时过流水头损失将较大,这种情况是不利的。另外,也存在已定的门体重量使得拍门的下落过程不能达到理想的状态。对上述两种均可采用增设平衡重的方法来解决。
增设平衡重的关键是正确选择外拉力点的位置。它不仅关系到平衡重的数值变化,而且对下落运动的过程及撞击力影响很大。
在使用计算图③时要求作到:
(1)当拍门开启角α为55°时,外拉力方向与过拍门吊点所作垂线的夹角β应为零。(可偏差±5°)
(2)当拍门下落至α=15°时,夹角β应为35°。(可以偏差±5°)
(3)如经变动外拉力点位置或由于允许范围所限,使其不能达到自角的上述要求时则按
计算出cosβ,值。再按 ![]() 计算出MF值。(a、b值为拍门上铰距外拉力点的水平、垂直距离)。
计算出MF值。(a、b值为拍门上铰距外拉力点的水平、垂直距离)。
计算图③是在上述要求的条件下,计算出开启角达50°、55°、60°、65°时平衡重的转矩值。例如:要计算开启到55°。的平衡重值,需找出图中MC (α=55°)的一侧数值,出图中MG(α=55°)的一侧数值,联线交MF坐标中55°一侧的数值,即为开启角为55°的平衡重转矩。再除以拍门上铰到外拉力吊点的距离,即为所求的平衡重值。(凡计算为负值即不需用平衡重便可达到该指定角度)
5.正流阶段时间的计算说明
首先用计算图④求出停机正流阶段机组所耗动能Wm,再用计算图⑤求出正流阶段所耗动能Wf,后用计算图⑥根据Wm+Wf值再求出正流时间TB值。
6.下落角速度的计算说明
计算图⑦可将不同流量,不同下落初始角、按不同门重求出下落至正流结束时的角速度值。
由于影响下落角速度的因素很多,角速度计算图中要全部包括各种变量是不现实的,图⑦仅表示Q=4~7米3/秒、门重500~1700公斤、开始下落角55°~80°时的部分状况。
图中所标出的角速度值是运用布里斯积分法所求出的。图⑦所不包括的范围,可按下列计算模式及电算程序计算:
(1)计算模式:
α″=aα′2 - b·sinα+c[1-(t/TB)]2 ·cos2α(正流阶段)
设步长为h,取n=(TB/h),运算至tn=TB停止
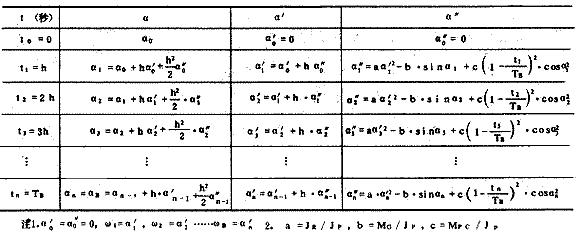
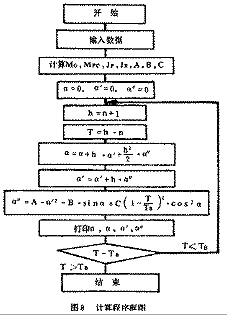
(2) 电算程序:
上述计算是采用布里斯积分法进行的。电算程序框图见图⑧。逆流阶段的计算模式及程序略。
在有平衡重进行下落角速度计算时,居平衡重F首先等效于门体重量、再计算出实际门重G与平衡重(等效于门重)之差值GO,查图⑦得下落角速度值ω。或按G0=G-1.7F式计算得近似值,由此查图求出ω近似值。
判断下降至终点时,处于正流还是逆流阶段的方法,见“拍门优化设计的电算程序”。若不具备此电算条件时,可用下述近似方法计算:将计算图所求出的ω值代入下式:
T=K1[0.1745/ω×下落初始角一下落终端角/10] ;
K1==0.88~0.92。所运算出的T值再与计算图⑥所求出TB值比较,T<TB则为正流,反之逆流。
至此,有关拍门开启及下落运动求解的说明已结束。拍门对门座撞击力的计算,主要运用上述诸图所求出的MG、MC 、MF、ω等值来进行。由于撞击力值还决定于接触缓冲用之橡皮面积、厚度和特性,鉴于各种橡皮特性及所选用的几何尺寸变化范围很大,不易用计算图直接表达。为此,撞击力的计算可按下式进行:
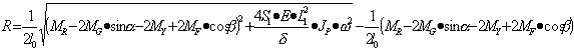
式中:
L0——拍门形心距拍门上铰轴距离;
MY——动水压力矩;在正流阶段MY =0;
cosβ——当选用计算图③所要求的条件时,cosβ=1;
MR——水体阻力矩:园形拍门:
MR=0.1717K·r-H![]() ·ω2;
·ω2;
矩形拍门:
MR=0.25K·r-Bo·H![]() ·ω2;
·ω2;
K——水体阻力系数,K=1.5~2.0;
r——水体密度;
B0——矩形拍门宽度;
H0——拍门全高;
E——橡皮弹性模量;
S1——橡皮接触面积;
δ——橡皮厚度;
L1——橡皮形心距上饺距:
JP——拍门体转动惯量、JP=(5G/16g).H02(KG-M-SEC2) ;
(此式适于园形拍门)
四、用法举例
已知一泵站:H=4米、Q=6米3/秒、流道出口处流速U=2.3米/秒、圆形拍门全高H0=2.5米、电机转数N=440转/分、机组转动惯量J=25公斤一米一秒2、出水管道中心线长度L=11米、出水管平均面积S=2.5米2、拍门体重量分布均匀,重心、形心距拍门上铰距为1.25米,拍门上铰距吊点距离L吊=1.9米。
方案一、设拍门门重G=1550公斤
查图①:
(1) Q=6、U=2.3、则Pc=1430
(2) Pc=1430、Lc=1.25、则Mc=1800
当 G=1550时,则浮力W=200、则G-W=1350
查图②:
(1) G-W=1350、Lg =1.25、则MG =1700
(2) MG =1700、MC =1800、则Y=0.9
(3) 过Y轴中的0.9点作Y轴垂线,交X于a
(4) 过a点作向α轴垂线,交轴得α=40°因开启角小于50°,故需查 图③:MG =1700、MC =1800
(1) 开启50°的MF (50)=480、开启55°的MF(55)=710、开启60°的MF (60)=900、开启65°的MF (65)=1100
(2)由于L吊=1.9米,故平衡重分别为:F(50)=252公斤、F(55)=374公斤、F(60)=474公斤、F(65)=579公斤。
查图④求停机正流时机组所耗动能:
(1) N=440、J=25、则Wm/T=46×105
(2)Wm/T=46×105 由此点作垂线交Wm 为a
(3)过a作斜线的平行线,交0.6ωH线为b
(4) 过b作垂线,交Wm =14.7×103
查图⑤求停机正流时流道所耗动能:
(1) L=11、S=2.5、则T=4.4
(2) T=44、Q=6、则Wf=72×102
查图⑥求停机正流阶段时间:
(1) H=4、Q=6、则T=24
(2) T=24、Ww+f=219×102、则交TB为a
(3) 过a作斜线的平行线、交η=0.8线于b
(4) 过b作垂线、交TB=1.7秒为所求。
计算角速度时,因有平衡重、故不能用门重G直接查图求出。应先将平衡重等效门重后再查图,其计算门重应为G0 =1550 -1.75F。
也即:α=50°时G0=1109公斤、α=55°时G0=895公斤
α=60°时G0=721公斤、α=65°时G0=537公斤
由计算图⑦可查出:当α=65°时,计算门重G0=537公斤、图中曲线中断,意味着门重过轻、下落转矩与水流冲力矩和阻力矩之和发生瞬刻平衡,直至逆流阶段方能下落。在逆流阶段下落的状况是不利的,应当尽可能排除。
当α=55°时,G0 =895公斤,故ω=0.425(K=2)
当α=60°时,G0 =721公斤,近似得ω=0.415(K=2)
判断此两种状况下落至终点处于何种阶段(正流、逆流),可用前述说明中的方法计算,即:
α=55°,T =0.9(0.1745/0.425)×(55-10)/10=1.66<1.7 为正流。
α=60°,T =0.9 (0.1745/0.415)×(60-10)/10=1.89>1.7为逆流。
上述查图计算可知:α=65°下落至终端时完全处于逆流阶段,是很不利的。α=60°下落至终端已开始逆流,撞击力在一定程度上也会加大。α=50°的开启角又稍偏小,仅α=55°状况是较好的。
上述即为所选方案计算的全过程。由于门体重量是拍门设计的一个关键变量,为此,可考虑变换门体重量,再作方案以比较。
方案二、设拍门门重G=950公斤
查图①:同上,MC =1800。当G=950时W=150,则G-W=800
查图②:
(1) G-w=800、Lg=1.25, 则MG =1000
(注:方案二在计算图中联线标记为Y′、2′………)
(2) MG=1000、MC =1800则Y=0.52
(3) 过Y轴上的交点作对Y轴垂线、交X于b
(4) 过b作α轴垂线,得α=51°
查图③:
(1) 当开启50°,MF (50°)=0,
当开启55°,MF (55°)=240,
当开启55°,MF (60°)=360,
当开启65°,MF(65°)=550
(2) 由于L吊=1.9米,故平衡重分别为:
F(50°)=0, F(55°)=126公斤
F(60°)=190公斤 F(65°)=289公斤
查图④、⑤、⑥同方案一。
查图⑦计算角速度时,不带平衡重时可用门重直接查图,带有平衡重时可等效门重后,再用计算门重查图。
当α=50°时, G0=G=950,α=55°时, G0=729,α=60°时, G0=617,α=65°时, G0=444
由计算图可查出当α=65°时,图中曲线中断,门重过轻,同方案一,这种状况是不利的。
当α=55°,G0=729公斤,可知ω=0.405 (K=2)
当α=60°时,G0=617,可近似得ω=0.395 (K=2)
当α=55°时,T=0.9(0.1745/0.405)×(55-10)/10=1.74秒,>1.7,虽时间稍大于TB值,但超出时间在半秒之内,可以看成为正流阶段接触门体。
当α=60°时,T=0.9(0.1745/0.405)×(55-10)/10=1.99秒>1.7,故为在逆流阶段下接触门体。两个方案对比如方安对比表。
综上四种开启角的八个方案中,以IV方案为好。它与Ⅲ方案比,虽都在正流阶段内下落,但其门重轻且下落至终点的角速度低,因而撞击力小。
将上述求出MG、MF 、ω等值代入撞击力公式计算即可。如E、S1、δ选取得当,撞击可控制在15吨左右。
方 案 对 比
方案
开启角
门重
平衡重
计算门重
角速度
正、逆
结论
Ⅰ
50°
1550
250
1109
偏大
正流
偏坏
Ⅱ
50°
950
0
950
偏小
正流
偏好
Ⅲ
55°
1550
374
895
0.425
正流
较好
Ⅳ
55°
950
126
729
0.405
正流
好
Ⅴ
60°
1550
474
721
0.415
逆流
不好
Ⅵ
60°
950
190
617
0.395
逆流
不好
Ⅶ
65°
1550
579
537
瞬态平衡,延迟下落
逆流
很不利
Ⅷ
65°
950
289
444
″
逆流
很不利
注:此篇论文发表在《中国给水排水》杂志,1985年第1期。
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 [email protected] ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








