城市给水管网可靠度的计算
赵新华1, 刘英梅1, 乔 宇2
( 1.天津大学环境科学与工程学院,天津300072;2.天津大学机械学院,天津 300072)
摘 要:研究了城市给水管网可靠度的计算,首先从可靠度与图论原理出发,阐释了算法设计的依据,然后从管网结构的角度,以最小路原理为依据,应用最小路不交化方法设计了给水管网可靠度的算法并进行了实例验证。
关键词:城市给水管网;可靠度;最小路;不交化
中图分类号:TU991.33
文献标识码:C
文章编号:1000-4602(2002)04-0053-03
? 以最小路不交化算法为核心,从管网的网络系统结构入手,分析管段的关联关系对管网可靠度的影响,采用遍历计算的方式,从单个管段的可靠度计算出管网中水源点与任意非水源点的可靠度,取最小值作为管网系统可靠性的评价。
1 计算依据
如果给定一个网络,将其整体作为一个系统、每条弧作为一个组件。系统可靠性理论的中心问题是要确定系统可靠度与其组件可靠度之间的关系。?
1.1 管网组件可用度A
给水管网在实际运行中经常出现管段故障的情况,经维修后仍投入正常运行,那么称这样的管段为可维修组件,其可靠度用组件可用度A表示。?
组件在规定的条件下,在任意时刻上正常工作的概率称为组件瞬时可用度A(t);与瞬时可用度相对应的是瞬时不可用度,表示组件在规定的条件下使用时任意时刻故障的概率用Q(t)表示,显然Q(t)=1-A(t)。?
采用组件瞬时可用度公式:?
![]()
式中 ?λ——管网的故障率?
μ——管网的修复率?
将组件可用度A定义为管段从开始到使用寿命T这一时间段内的平均可用度,即求A(t)的数学期望E[A(t)]。由函数的数学期望公式得:?
![]()
又因为f(t)在[0,T]时间段内服从均匀分布,f(t)=1/T、t∈[0,T],故组件可用度的数学式表示为:
![]()
相应的组件不可用度Q=1-A。?
1.2 管网系统可靠度
在研究系统可靠性时,首先对所研究的对象作4点假设:?
① 组件和系统都只有正常和失效两种状态;?
② 系统的状态完全由系统的逻辑关系和组件的状态决定;?
③ 组件的状态转移率即故障率λ和修复率μ均为常数;?
④ 组件或系统的故障和修复都相互独立。?
采用最小路不交化算法求解。设G是一个给定的网络,V1、V2是指定的两个节点,则基本问题是求时刻T由输入节点V1可以到达输出节点V2的概率,亦即求时刻T系统正常的概率R。?
对网络的路及最小路的定义如下:?
定义1对于给定网络G,从指定的节点V1经过一串弧序列(或其中的一部分弧)可以到达节点V2,则称这个弧序列为从V1到V2的一条路。?
定义2对于给定网络G,从节点V1到V2的弧序列称作一条最小路,若满足①它是一条路,②最小性,即从这个弧序列中除去任意一条弧后它即不是从V1到V2的路。?
由于系统正常这一事件可表示为S={V1可以到达V2}={由V1至少有一条最小路通到V2},这里最小路是指组成这条最小路的弧都正常这一事件。因此,若记A1,A2,…,Am为网络的所有最小路,则![]() ,,即将求可靠度问题转化为求随机事件和的问题。?
,,即将求可靠度问题转化为求随机事件和的问题。?
由概率论可知:![]() 称为容斥定理 。?
称为容斥定理 。?
若能把系统正常这一事件表示成不交(即相斥)事件之和![]() 称为相斥求和公式。?
称为相斥求和公式。?
当最小路数目不多时,用直观方法可以得到全部最小路;若系统结构复杂,产生的最小路数目较多时,应采用图论中的邻接矩阵法[1、2]求全部最小路。用最小路不交化方法将相依事件转化为相斥事件,然后利用相斥求和公式求解系统的可靠度,从而简化了计算过程。?
定理1设A1,KAm为网络G的所有最小路,A1,L,Ar的长度都小于n-1,Ar+1,L,Am的长度为n-1,且r<m,则:
![]()
其中右端![]() 、Br+1、L、Bm之间不交,而Br+1、L、Bm为Ar+1、L、Am中分别添上在其中不出现的(l-n+1) 条弧的逆而成之事件。?
、Br+1、L、Bm之间不交,而Br+1、L、Bm为Ar+1、L、Am中分别添上在其中不出现的(l-n+1) 条弧的逆而成之事件。?
2 算法设计
对于已知结构的管网系统,每个水源点与每个非水源点之间的系统可靠度都可以采用最小路不交化算法求得,即:将水源点处理为输入节点,非水源点处理为输出节点,采用邻接矩阵法求得网络的所有最小路,并对所求得的所有最小路进行不交化处理,就可以结合组件的可用度进行此时的系统可靠度计算。?
假设管网的管段可用度Ax与管段不可用度Qx均已求出,且通过邻接矩阵分析已知A1,KAm为管网G中水源点i与非水源点j之间的所有最小路,A1,L,Ar的长度都小于n-1,Ar+1、L、Am的长度为n-1,则其系统可靠度R的计算过程如下:
① 挑出长度为n-1的最小路全体Ar+1、KAm,利用公式![]() 将求集合并的问题简化为求代数和的形式,Bi是指在Ai中添上在其中不出现的(l-n+1)条弧的逆而成之事件,Bi之间不交,其概率之和作为系统可靠度的一部分,即最小路长度为n-1子集的可靠度R1。?
将求集合并的问题简化为求代数和的形式,Bi是指在Ai中添上在其中不出现的(l-n+1)条弧的逆而成之事件,Bi之间不交,其概率之和作为系统可靠度的一部分,即最小路长度为n-1子集的可靠度R1。?

循环计算,其中每一步使Aj与A1、L、Aj-1、不交,j=2,……,r(r为集合元素数)。
d.?F中还有项(即rk+1≥1)吗?若有,则K←K+1,转b步骤),否则结果R2就作为系统可靠度的另一部分。
③ R=R1+R2即为系统可靠度,任一条不交化最小路Bi=x1Lxn-1xnLxl的概率为:P{Bi}=Ax1LAxn-1QxnLQxl。
在分别考虑了每个非水源点与水源点之间的系统可靠度后,给水管网的可靠度取其中的最小值,即最不利点的系统可靠度。?
3 实际算例
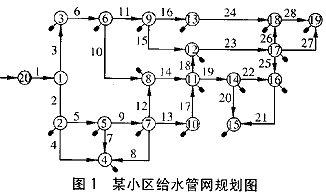
某市一小区给水管网的规划设计,管网共有20个节点,其中有一个水源点、19个用水点和28条管段(见图1),设计供水能力为131 L/s左右,全部管段采用DN100~DN500的铸铁管铺设。?
故障率λ定义为单位时间单位长度管线发生故障的次数。对该市多年的经验数据进行统计,确定的管道故障率λ值见表1。
修复率μ定义为单位时间管道维修的次数。根据该市大量管道维修业务台帐进行统计,对于DN300及DN300以下的管道修复率取1095次/a,对于DN300以上的管道修 复率取730次/a。
本算例采用的时间段T值为5 A,从计算结果(表2)可见该小区的管网很可靠,即管段比较可靠和管网的网络结构合理。在管网的运行中各个管段相互关联,后者对于管网的改扩建工作尤其有重要意义,因为在不过多改变管径的前提下,通过提高管网的连通性来提高管网的可靠性是既节约成本又保证管网可靠性的好方法。
4 结语
从管网静态结构出发计算了管网系统的可靠度,并利用实际管网的结构参数进行了验证,证明了算法的有效性,但还需进一步研究的问题如下:?
① 改进现有算法,引入稀疏矩阵、并行计算等方法以提高运算速度,利于大型管网的计算研究。?
② 结合管网运行的动态性计算管网的水力可靠度,但是水力可靠度的分析与结构可靠度的分析是密不可分的,需要找到它们之间的综合关系,进行管网系统可靠性的整体评价。?
③ 若把可靠度的计算与管网改扩建工作的综合规划相结合,将发挥更大的作用。
参考文献:
[1]阿布拉莫夫H H.给水系统可靠性[M].北京:中国建筑工业出版社,1990.
[2]Rajesh Gupta.Reliability analysis of water-distribution systems[J].Journal of Environmental Engineering,120(2):447-460.
[3]Bao Y,Mays L W.Model for water-distribution system reliability[J].Journal of Hydraulic Engineering,116(11):1119-1137.
电 话:(022)27400830
收稿日期:2001-10-11
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 [email protected] ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








