惯性效应在混凝中的动力学作用
摘 要 本文首次从湍流微结构的尺度即亚微观尺度对混凝的动力学问题进行了研究,提出了惯性效应是絮凝的动力学致因;提出了湍流剪切力是絮凝反应中的决定性的动力学因素,并建立了絮凝的动力相似准则。文章指出扩散过程应分为宏观扩散与亚微观扩散两个不同的物理过程,而亚微观扩散的动力学致因是惯性效应,特别是湍流微涡旋的离心惯性效应。
关键词:混凝动力学致因,惯性效应,亚微观传质,相似准则
Kinetic Functions of Inertia Effects in coagulation Process
ABSTRACT:The paper for the first time studied coagulation kinetics in the dimention digits of turbulence micro-structures, i.e., the submicro dimention digits. It brought up the idea that inertia ffect is the kinetic cause of floccula-tion , qnd the shear force of turbulent flow is the dominant inetic factor in floc-culation process. It also established the kinetic laws of similitude of locculation. The whole dispersion process ought to be divided into two physical processes, macrodispersion and submicrodispersion. The kinetic cause of submicro-dispersion is the inertia effect, especially the centrifugal inertia effect of the microeddy of tubulent flow.
KEY WORDS: kinetic causes of coagulation, inertia effects, sub-micro mass transfer, similitude rules
1、絮凝动力学的研究现状
絮凝长大过程是微小颗粒接触与碰撞的过程。絮凝效果的好坏取决下面两个因素:(1)是混凝剂水解后产生的高分子络合物形成吸咐架桥的联结能力,这是由混凝 剂的性质决定的;(2)是微小颗粒碰撞的几率和如何控制它们进行合理的有效碰撞,这是由设备的动力学条件所决定的。导致水流中微小颗粒碰撞的动力学致因是什么,人们一直未搞清楚。水处理工程学科认为速度梯度是水中微小颗粒碰撞的动力学致因,并用下面公式计算速度梯度:
G=(P/μ)1/2 [3]
式中为单位水体的能耗;μ为液体的动力粘滞系数。由于上面公式是在层流的条件下导出的,它是否适用于流态是湍流的絮 凝池一直是人们所关心的。这一问题一直未有结论。实际上,上面公式是层流条件下的速度梯度。对于湍流来说由于湍动涡旋的作用,大大地增加了湍流中的动量交换,大大地均化了湍流中的速度分布。所以湍流中的速度梯度远远小于上式计算的数值。既然如此,上面公式在给水处理的工程界中为什么可以用了半个世纪呢?因为上面公式中P(单位水体能耗)这一项与湍流中的微涡旋有着密切关系,从后面文章内容我们可以看到,正是这些湍流的微 结构决定了水中微小颗粒的动力学特性和它们之间的碰撞。通过几十年的工程实践人们积累了上面公式大量的经验数据,用此来指导工程设计当然不会出现大的问题。但上还公式对改善现有的絮凝工艺并没有任何价值。因为提高絮凝效果就必须增加水中颗粒的碰撞几率。按照上述的速度梯度理论可知,要想增加碰撞几率就必须增加速度梯度,增加速度梯度就必须增加水体的能耗,也就是增加絮凝池的流速。但是絮凝过程是速度受限过程,随着矾花的长大,水流速度应不断减少。
另一方面我们可以举出一个完全与速度梯度理论相矛盾的絮凝工程实例。网格反应池在网格后面一定距离处水流近似处于均匀各向同性湍流状态,即在这个区域 中不同的空间点上水流的时平均速度都是相同的,速度梯度为零。按照速度梯度理论,速度梯度越大,颗粒碰撞次数越多。而网格絮凝反应池速度梯度为零,其反应效率应最差。事实恰好相反,网格反应池的絮凝反应效果却优于所有传统反应设备。这一工程实例充分说明了速度梯度理论远未揭示絮凝的动力学本质。
在絮凝的研究中,还有一个湍流研究学派用湍流扩散的时平均方程去计算颗粒碰撞次数。最后得到的结论与速度梯度理论基本相同,即湍流中颗粒碰撞次数随湍流能耗增大而增大。由于这种研究方法用的是湍流扩散时平均方程,因此就不能揭示湍流微结构在絮凝中的动力学作用。在诸如象絮凝动力学的研究中,把研究领域仅仅划分为微观与宏观已不够了。因为絮凝中的颗粒碰撞是与湍流中的微结构的动力作用密切相关,而微观研究领域的分子尺度远远小于湍流中的微结构尺度,所以微观的分子运动完全不受湍流微结构影响,只与热力学系参数有关。而宏观流动计算中人们关注的是时平均速度,时平均压强、时平均浓度,无法去揭示湍流微结构在絮凝中的动力学作用。因此在絮凝动力学的研究中应从湍流微结构的尺度,即从亚微观尺度上进行研究。上述絮凝的湍流研究学派正是因为采用统计时平均的宏观流动计算方法,所以就无法揭示絮凝的动
2.絮凝的动力致因
有人认为湍流中颗粒碰撞是由湍流脉动造成的。这种认识不很确切。实际上湍流并不存在脉动,所谓的脉动是由于所采用的研究方法造成的。人们用流体力学传统的研究方法欧拉法进行研究,即在固定的空间点观察水流运动参数随时间变化,这样不同时刻有不同大小的湍流涡旋的不同部位通过固定的空间点,因此在固定的空间点上测得的速度呈现强烈的脉动现象。如果我们跟随水流质点一起运动,去观察其运动情况,就会发现水体质点的速度变化是连续的,根本不存在脉动。实际上水是连续介质。水中的速度分布是连续的,没有任何跳跃。水中两个质点相距越近其速度差越小,当两个质点相距为无穷小时,其速度差亦为无穷小,即无速度差。水中的颗粒尺度非常小,比重又与水相近,故此在水流中的跟随性很好。如果这些颗粒随水流同步运动,由于没有速度差就不会发生碰撞。由此可见要想使水流中颗粒相互碰撞,就必须使其与水流产生相对运动,这样水流就会对颗粒运动产生水力阻力。设颗粒的形状为球形,其半径为r0,颗粒与水流相对速度为υ,水的密度为ρ,球形颗粒所受水力阻力Fd可按下式计算
Fd=Cdπr02(ρυ2/2)
式中:Cd为水流的绕流阻力系数
单位质量球形颗粒所受的水力阻力fd 为
fd=[Fd/(4/3πγ03)]=3Cdρυ2/8ρ0r0 [2]
式中ρ0为球形颗粒密度。如果略去因颗粒尺寸不同而造成的密度变化,由上式可见单位质量球形颗粒所受水力阻力随尺度增 大而减少;即颗粒越大单位质量所受水力阻力越小。上面讨论虽然是针对球形的,但对非球形颗粒同样适用。由于不同尺度颗粒所受水力阻力不同,所以不同尺度之间就产生了速度差。这一速度差为相邻不同尺度颗地的碰撞提供了条件。如何让水中颗粒与水流产生相对运动呢?最好的办法是改变水流的速度。因为水的惯性(密变化时它们的速度变化(加速度)也不同,这就使得水与其中固体颗粒产生了相对运动。为相邻不同尺度颗粒碰撞提供了条件。
改变速度方法有两种:(1)是改变水流时平均速度大小,水力脉冲澄清池、波形反应池、孔室反应池以及滤池的微絮凝作用主要就是利用水流时平均速度变化造成的惯性效应来进行絮凝;(2)是改变水流方向,因为湍流中充满着大大小小的涡旋,因此水流质点在运动时不断地在改变自己的 运动方向。当水流作涡旋运动时在离心惯性力作用下固体颗粒沿径向与水流产生相对运动,为不同尺度颗粒沿湍流涡旋的径 向碰撞提供了条件。不同尺度颗粒在湍流涡旋中单位质量所受离心惯性力是不同的,这个作用将增加不同尺度颗粒在湍流涡旋径向碰撞的几率。下面来讨论这个问题。在湍流涡旋中取一个小的脱离体,显然沿径向方向作用在该脱离体上有两个力,一是离心力;二是压力的合力。两者相平衡。如果把坐标原点取在运动的涡旋的中心上,则可写成如下方程:
![]()
式中r为涡旋半径;υθ为脱离体处涡旋的切向速度;公式左侧为作用在脱离体上压力合力,右侧为脱离所受的离心惯性力。设 想与脱离体同一位置有一固体颗粒,如果它与水流同步运动,它所受的压力合力与上面一样,由于它等于脱离体所受离心力,故可以写成。ρ(υθ2/r)。该固体颗粒所受的离心力为ρ0(υθ2/r)。故该固体颗粒所受净离心力(离心力与压力之差)为(ρ0-ρ)υθ2/r [2]
固体颗粒在其作用下沿涡旋的径向运动。因为固体颗粒所受的水力阻力即为液体对其拖动力。而固体颗粒单位质量所受 的水力阻力随尺度增大而减少,即颗粒尺度越大,单位质量所受拖动力越小。因此颗粗尺度越大其跟随性越差,即其速度与其所在地液体的速度差别越大,单位质量所受离心力越小,这样必然有这样一种情况,在一个特定的湍流涡旋中的某一个地方必然有一个特定颗粒直径Dc,它所受的离心力与压力合力正好相等。当颗粒尺度<Dc时,颗粒在离心力作用下沿涡旋径向向外侧运动;当颗粒直径>Dc时颗粒在压力作用下向涡旋内侧运动。这一作用加大了不同尺度颗粒沿径向碰撞的几率。
颗粒沿涡旋径向碰撞的几率随涡旋的离心惯性力的加大而加大这是显然。用λ表示涡旋尺度的特征值,用ε表示单位水体的能耗。因此可用下式计算涡旋的雷诺数Rew=υ·λ/v,式中v=μ/ρ为水的运动粘滞系数。涡旋雷诺数表示涡旋的惯性力与粘 性力之比。当两者相等时的涡旋尺度特征值λ0满足,υ·λ0/v=1从理论上可以推出,λ0=(ε0/v)1/4,式中ε0=ε/ρ为单位质量水体的能耗。当涡旋尺度λ>>λ0,涡旋中的惯性力是主要的,粘性力可略去。此时涡旋中速度的特征值υλ主要与ρ、λ、ε三个因素有关,用这三个因素可以组成一个速度因子(其有速度因次),(ελ/ρ)1/3,可以认为υλ量级由 这一速度因子决定,表示为υλ~(ελ/ρ)1/3而当λ<λ0时,涡旋中粘性力起主要作用,此时应用υ与λ形成速度因子,故
υλ~(υ/λ)
当λ>λ0时,涡旋的特征周期Tλ只与λ、ε、ρ有关,其量级可用由三者形成的时间因子 (λ2ρ/ε)1/3来决定,即
Tλ~(λ2ρ/ε)1/3
而涡旋的速度特征值
υλ~dλ/dT~λ/Tλ
涡旋的加速度特征值
αλ~dυλ/dT~υλ/Tλ~ε02/3/λ1/3
由上式可见涡旋的加速度(单位质量惯性力)随涡旋尺度减少而增加。也就是说涡旋越小,其惯性力越强。当涡旋尺度特征值达到λ0时,其加速度最大,惯性效应最强。由此可见湍流中的微小涡旋的离心惯性效应是絮凝的重要的动力学致因。在初期絮凝中λ0量级的涡旋起了重要的作用。
由上面的理论论述可以看出,如果能在絮凝池中大幅度度地加湍流微涡旋的比例,就可以大幅度地增加颗粒碰撞次数,有效地改善絮凝效果。这可以在絮凝池的流动通道上增设多层小孔眼格网的办法来实现。由于过网水流的惯性作用,使过网水流的大涡旋变成小涡旋,小涡旋变成更小的涡旋。不设网格的絮凝池湍流的最大涡旋尺度与絮凝池通道尺度同一数量级。当增设格网之后,最小涡旋尺度与网眼尺度同一数量级。
增设小孔眼格网之后有如下作用:(1) 水流通过格网的区段是速度激烈变化的区段,也是惯性效应最强,颗粒碰撞几率最高的区段;(2)小孔眼格网之后湍流的涡旋尺度大幅度减少,微涡旋比例增强,涡旋的离心惯性效应增加,有效地增加了颗粒碰撞次数;(3)由于过网水流的惯性作用,矾花产生强烈的变形,使矾花中处于吸附能级低的部分,由于其变形揉动作用达到高吸能级的部位,这样就使得通过网格之后矾花变得更密实。
3.矾花的合理的有效碰撞
要达到好的絮凝效果除有颗粒大量碰撞之外,还需要控制颗粒合理的有效碰撞。使颗粒凝聚起来的碰撞称之为有效碰撞。如果在絮凝中颗粒凝聚长大得过快会出现两个问题:(1)矾花长得过快其强度则减弱,在流动过程中遇到强的剪切就会使吸咐架桥被剪断,被剪断的吸咐架桥难再连续起来,这种观象称之为过反应现象,应该被绝对禁止;(2)一些矾花过快的长大水中矾花比表面积急剧减少,一些反应不完善的小颗粒失去了反应条件,这些小颗粒与大颗粒碰撞几率急剧减小,很难再长大起来。这些颗粒不仅不能为沉淀池所截留,也很难为滤池截留。絮凝池中矾花颗粒也不能长得过慢,矾花长得过慢虽然密实,但当其达到沉淀池时、还有很多颗粒没有长到沉淀尺度,出水水质也不会好。由此看到在絮疑池设计中应控制矾花颗粒的合理长大。
矾花的颗粒尺度与其密实度取决两方面因素:其一是混凝水解产物形成的吸咐架桥的联结能力;其二是湍流剪切力。正是这两个力的对比关系决定了矾花颗粒尺度与其密实度。混凝剂性质决定的,而湍流的剪切力是由构筑物创造的流动条件所决定的。如果在 絮凝池的设计中能有效的控制湍流剪切力,就能很好的保证絮凝效果。
应该指出,水处理领域内流动的动力相似并没有真正建立起来。很多的小试、中试的试验结果在生产试验上无法重视,尺度放大后其流态发生了变化,甚至是根本的变化。由于人们对其决定性的动力学因素认识不清,就不知控制什么样的动力学因素,故此也就不能真正建立起水处理工艺中的动力相似。由上面讨论我们看到湍流剪切力是絮凝过程中的控制动力学因素,如果在大小两个不同的絮凝工艺中,其湍流剪切力相等,那么具有同样联结强度的矾花颗粒可以在两个不同尺度的絮凝过程中同时存在。这在某种意义上也就实现了两个絮凝过程絮凝效果的相似。湍流剪切力是由湍流涡旋造成的。设想一个矾花位于湍流涡旋之中,由于此涡旋外侧流速大,内侧流速小,因此位于其中的矾花颗粒受剪,此剪切力主要取决于涡旋尺度与涡旋强度。显然涡旋尺度越小,涡旋强度越大,涡旋对矾花的剪切作用越强。湍流中充满着大量大大小小的涡旋,因此涡旋尺度是随机的。这里所说的涡旋尺度可用均匀各向同性湍流中涡旋尺度统计特征物理量涡旋积分比尺代表,可以认为它是湍流中最大涡旋的特征尺度。它主要取决于流动空间尺度与流动速度两个因素。流动空间越大,涡旋尺度越大;在同一空间尺度下流动速度越大,涡旋尺度越小。由此可以认为湍流剪切力与流动空间尺度成反比,与流动速度成正比。而涡旋强度与流动速度成正比,这样就有下面关系。
湍流剪切力~υ2/L
式中υ为水流的特征速度;L为流动空间特征尺度。这样湍流剪切力的大小可用上面两个宏观物理组成的弗罗德数Fr=υ2/gL [2]来确定。实际上Fr本身就是相似似准则数,Fr 就表明了水流中惯性力与重力的对比,在地表面重力是一个常数,因此Fr表明了惯性力大小。显然,在一个固定的空间中惯性力越大,其湍流剪切力越大。所以Fr表明湍流剪切力的大小。两个尺度不同的絮凝过程当其Fr相等时,其湍流剪切力就相等。因此其絮凝效果就基本相似,这已为大量的小试、中试与生产试验所证实。
严格地讲,只控制湍流剪切力相等并不能完全控制絮凝效果的相似,因为湍流剪切力相等时两个不同的絮疑过程的矾花联结强度相等。但矾花的密实度与沉淀性能却不一定相同,矾花的密实程度可用湍动度σ来控制:
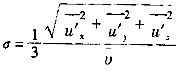
式中,u′x,u′y,u′z为空间点沿x、y、z方向的脉动速度;υ为空间点的时平均速度。显然。值越大表明在固定时间内流过固定空间 点的涡旋数量越多,涡旋强度越大,矾花也越密实。在实际工程中是不可能测定σ的。庆幸的是当湍流剪切力相等时,即当Fr相等时,尺度越大的絮凝池其水流速度也越高,因此矾花的碰撞强度越大,形成的矾花越密实,这已为试验与生产实践所证实。这样就可以保证把小尺度的试验结果按照Fr相等来放大,放大后的絮凝效果会更好、更可靠。
4.混合与初级混凝
混合是反应第一关,也是非常重要的一关。在这个过程中应使混凝剂水解产物迅速地扩散到水体中的每一个细部,使所有胶体颗粒几乎在同一瞬间脱稳并凝聚这样才能得到好的絮凝效果。因为在混合过程中同时产生胶体颗粒脱稳与凝聚,可以把这个过程称为初级混凝过程。但这个过程。混合问题实质上是混凝剂水解产物在水体中扩散问题。其扩散系数目由下面两个公式计算:
K~α(ε0λ)1/3λ [1] (λ>λ0)
K~β[(ε0/v)λ]1/2 [1] (λ<λ0)
式中α、β是两个待定系数。由上面公式可以看到,当研究范围尺度在λ>λ0与λ<λ0 与两种不同情况下其扩散系数的规律截然不同,而且当研究尺度λ越大时,其扩散系数越大,当λ越小时其扩散系数越小,当研究的尺度差别很大时,扩散系数可以差几个数量级。这样混凝剂水解产物在混合设备中的扩散应分为两类:(1)宏观扩散,即使混凝剂水解产物扩散到水体各个宏观部位,其扩散系数很大,这部分扩散是由大涡旋的动力作用导致的,故此宏观扩散可以短时间内完成;(2)亚微观扩散,即混凝剂水解产物在极邻近部位的扩散,这部分扩散系数比宏观扩散小几个数量级。亚微观扩散的实质是层流扩散。因此使混凝剂水解产物扩散到水体每一个细部是很困难的。在水处理反应中亚微观扩散是决定性作用的动力学问题。在高浊水的处理中混凝剂水解产物的亚微观扩散成为控制处理效果的决定性因素。由于混凝剂的水解产物向极邻近部扩散的速度非常慢,在高浊期水中胶体颗粒数量非常多,因此没等混凝剂水解产物在极邻近部位扩散,就被更靠近它的胶体颗粒接触与捕捉。这样就形成高浊时期有些地方混凝剂水解产物局部集中,而有些地方还根本没有。混凝剂局部集中的地方矾花迅速长大,形成松散的矾花颗粒,遇到强的剪切力吸附桥则被剪断,出现了局部过反应现象。药剂没扩散到的地方胶体颗粒尚未脱稳,这部分絮凝反应势必不完善,这一方面是因为它们跟不上已脱稳胶体颗粒的反应速度,另一方面是因为混凝剂集中区域矾花迅速不合理长大,也使未脱稳的胶体颗粒失去了反应碰撞条件。这样就导致了高浊时期污泥沉淀性能很差,水厂出水水质不能保证。按传统工艺建造的水厂,在特大高浊时都需大幅度降低其处理能力,以保证出水水质。由于过去工程界的人们对亚微观传质 现象不认识,对其传质的动力学致因也不认识,因此传统的混合设备无能力解决高浊时混合不均问题,这不仅使水厂在特大高浊时大幅度降低处理能力。而且造成药剂的严重浪费和造成出水的pH值过低。
亚微观扩散究其实质是层流扩散,其扩散规律与用蜚克定律描写的宏观扩散规律完全不同。当研究尺度接近湍流微结构尺度时,物质扩散过程不一定是从浓度高 的地方往低的地方扩散。在湍动水流中亚致的物质迁移造成的,特别是湍流微涡旋的离心惯性 效应。我们发明的串联管式初级混凝设备和管式微涡初级混凝设备,就是利用高比微观传质阻力,增加亚微观传质速率。生产使用证明这两种设备在高浊时混合效果良好,不仅比传统的静态混合器可大幅度增加处理能力,也大大地节省了投药量。
结 论
本文首次从湍流微结构的尺度(即亚微观尺度)讨论了流动水体中颗粒碰撞(物相接触)和混凝剂水解产物的亚微观传质这两个物理过程及其动力学致因,这正是混凝过程和多相流动物系反应过程中最重要的动力学规律,也是其动力学的核心问题。目前在各个工业领域的多相流动物系反应工艺中,其反应不是化学反应就是生化反应。众所周知,化学反应速度非常迅速,生化反应在生物酶存在的情况下,其反应速率也远大于物相接触,特别是远大于亚微观传质的速率。因此在这些工艺过程中提高物相接触和亚微观传质速率就成为提高工艺效率和工艺品质的关键。可以预见本文所揭示的自然规律必将对其相关领域的工艺进步起到重要的推动作用。
参考文献
[1]列维奇 理化学流体力学科技出版社
[2]王绍文 论絮凝的动力学致因 给水与废水处理国际会议论文集
[3]王绍文 涡旋混凝低麦冬沉淀给水处理技术工作机理水与废水技术研究


论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 [email protected] ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








