给水管网计算中的数据转换方法
王国明
(合肥工业大学土木学院,安徽合肥 230009)
摘 要:在给水管网计算中,通过建立环-管段矩阵、环-节点矩阵以及输入节点流量、节点坐标等少量数据,通过计算和数据转换,便可求得经济管径、管段设计流量、节点水压值、水厂供水量、管网造价、年费用折算值等。采用该方法进行管网计算,可以减少40%—70%的计算时间。
关键词:给水;管网;管网计算;数据转换
中图分类号:TP391.75;TU99.36.
文献标识码:A
文章编号:1009-2455(2002)06-0044-03
A Method for Data Conversion in Calculating Feed Water Network WANG Guo-ming
(College of Civil Construction Engineering, Hefei University of Technology, Hefei 230009, China)
Abstract: In calculating feed water network, after establishing the loop-pipe segment matrix and loop-node matrix and inputing a few data, such as nodal flow and nodal coordinates, economic pipe diameter, pipe segment design flow, nodal water pressure, supplied quantity of water from water plant, network construction cost, con-version value of annual cost, etc., can be obtained through calculation and data conversion. 40%——70% of cal-culation time can be saved by using this method in the calculation of the network.
Key words: feed water; network; network computation; data eonversion
在《给水环网计算程序中的数据转换方法》[1]的基础上,经过摸索和研究,发现管网图形的基本关系可以用管网基本关系矩阵来表示,并且管网的其它关系矩阵可以由基本关系矩阵派生。这样就可以大大地减少输人数据量,利于实现快速计算。现介绍如下:
1 给水管网图形数据
给水管网图形可以看成由管段、节点、环等组合而成的集合。利用计算机进行给水管网计算时,必须把给水管网图形中的有关数据输入到计算机中。
在图1的管网中,有Ⅰ,Ⅱ两个环。Ⅰ号环有4个管段,Ⅱ号环有3个管段,各管段按顺时针方向编上环内局部号:Ⅰ号环有(1),(2),(3),(4)管段,Ⅱ号环有(1),(2),(3)管段。管网管段的总体编号为1,2,3,4,5,6。
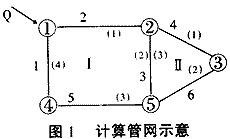
根据图1可以写出各种关系矩阵如下:
1.1 管段局部号与总体号转换矩阵LC(I,J)
管段局部号与总体号转换矩阵LC(I,J)也可以称为环一管段(转换)矩阵。LG(I,J)的值为管段总体号,下标I为环号,J为环内管段局部号。
![]()
1.2 节点一管段转换矩阵KL(Ⅰ,J)
节点一管段转换矩阵KL(Ⅰ,J)也可以称为环-节点(转换)矩阵。KL(Ⅰ,J)的值为节点号,下标Ⅰ为环号,J为环内管段局部号并增加1号。
![]()
1.3 环一环转换矩阵ⅠL(Ⅰ,J)
环一环转换矩阵ⅠL(Ⅰ, J)也可以称为管段识别矩阵。ⅠL(Ⅰ,J)的值为邻环的环号,下标Ⅰ为环号,J为环内管段局部号。ⅠL(Ⅰ,J)=0表示第Ⅰ环内第J号管段是边界管段,无邻环。
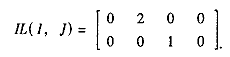
实际的计算要求图形信息具体,输入量少。因此,必须找出能反映管网图形中节点、管段和环之间相互关系的最少数的矩阵,并且使之能派生出其它的有关矩阵。不妨称这最少数的矩阵为基本关系矩阵。
2 给水管网图形数据的转换
如果在计算之前要输入计算中将用到的各种数据,那末输人的数据量比较大。如果采用数据转换方法就可以减少输入数据的量。数据转换是依靠采用各种转换矩阵来实现的。要达到好的效果,选择合适的转换矩阵是关键[1]。根据分析,管网图形中管段、节点、环这三者之间的关系,可以用两个基本关系矩阵来表达。其余的关系矩阵可以由这两个基本关系矩阵派生。以下选择“管段局部号与总体号转换矩阵”和“节点一管段转换矩阵”作为基本关系矩阵,来说明派生的方法。
2.1 由基本关系矩阵派生“环--环转换矩阵”
环—环转换矩阵ⅠL(Ⅰ,J)的值为第Ⅰ环第J管段的邻环号,它可由管段局部号与总体号转换矩阵LG(Ⅰ,J)派生出来。以图1管网为例,![]() ,它的第1行第2列的元素3和第2行第3列的元素3相同,而其他的元素没有这样的情况;因此反映出管段识别矩阵的第1行第2列元素和第2行第3列元素对应了同一管段,即两环共有管段,而其他管段都不是两环共有管段;于是环-环转换矩阵为
,它的第1行第2列的元素3和第2行第3列的元素3相同,而其他的元素没有这样的情况;因此反映出管段识别矩阵的第1行第2列元素和第2行第3列元素对应了同一管段,即两环共有管段,而其他管段都不是两环共有管段;于是环-环转换矩阵为![]() ,因为LG(Ⅰ, J)矩阵中行号与管网图中环号相同,所以第1行和第2行的元素相同也就是第1行(第1环)和第2行(第2环)共有某一管段,从而第1环中该管段的邻环号为2,第2环中该管段的邻环号为1;其他管段都不是两环共有管段,没有邻环,邻环号为0。这样环一环转换矩阵ⅠL(Ⅰ,J)由管段局部号与总体号转换矩阵LC(Ⅰ,J)派生出来了。
,因为LG(Ⅰ, J)矩阵中行号与管网图中环号相同,所以第1行和第2行的元素相同也就是第1行(第1环)和第2行(第2环)共有某一管段,从而第1环中该管段的邻环号为2,第2环中该管段的邻环号为1;其他管段都不是两环共有管段,没有邻环,邻环号为0。这样环一环转换矩阵ⅠL(Ⅰ,J)由管段局部号与总体号转换矩阵LC(Ⅰ,J)派生出来了。
把派生的方法归纳如下:从管段局部号与总体号转换矩阵LG(Ⅰ,J)中检查是否有相同的元素,如果有则把各元素的行号互换填人各自所在的位置,即如果LC(Ⅰ, J)中第Ⅰ行第K列的元素和第J行第M列的元素数值相同,则在ⅠL(Ⅰ,J)中第Ⅰ行第K列填入J,在第J行第M列填入Ⅰ;如果没有数值的元素则在这些元素所在的位置填上0,即如果LC(Ⅰ,J)中第Ⅰ行第K列的元素值和其它各元素的值不相同,则在ⅠL(Ⅰ,J)中第Ⅰ行第K列填入0;如此处理得到环-环转换矩阵ⅠL(Ⅰ,J)。该方法可以编成程序,由计算机自动执行。
2.2 由基本关系矩阵派生A矩阵[2]
用计算机分配初始流量要涉及生成系数矩阵A和求解线性方程组[2]。因此在计算之前要输入系数矩阵A,其数据量很大。
为此可以由节点一管段转换矩阵KL(Ⅰ,J)派生A矩阵。方法如下:
以图1管网为例,A矩阵为:

其值为第Ⅰ环第J管段首节点号。在KL(Ⅰ,J)的每一行中,相邻两元素为相连接的节点号。因此检查KL(Ⅰ,J)每一行中各相邻两元素的节点号,不妨假设为K、M,则该对节点号K、M和M、K,即为系数矩阵A的某一元素的位置,在该位置(K,M)和(M,K)给以数值-1。因为A矩阵是对称矩阵,所以点对(K,M),(M,K)也是对称的。在系数矩阵A中,除了对角线上的元素和节点号相连接的元素之外,剩下的就是节点号不相连接的元素,其值为0。在系数矩阵A的对角线上的元素,其值为系数矩阵A的每一行中各个元素值之和的负数。这样就生成了A矩阵。该方法也可以编成程序,由计算机自动执行。
2.3 基本关系矩阵在管网计算中的应用
2.3.1 应用遗传算法时的数据转换
在应用遗传算法时,先要给第一代的每一个个体的各个基因编码,该编码对应了该基因所代表管段的管径。因此,每一代各个个体所有基因的编码就是对应管网所有管段的管径。显然,这是用总体号排列的各管段的管径。如果我们的平差程序是用以环为主线的思路编成的,那末必须把管段总体号转换为各个环中的管段局部号。设用总体号表示的管长与管径分别为LL(Ⅰ),KKD(Ⅰ);用局部号表示的管长与管径分别为L(Ⅰ,J),KD(Ⅰ, J)。采用管段局部号与总体号转换矩阵LC(Ⅰ, J),则把管段总体号转换为管段局部号的程序如下:
DO 21 Ⅰ=1,N
DO 21 J=1,LOTN(Ⅰ)
K=LG(Ⅰ,J)
L(Ⅰ,J)=LL(K)
21 KD(Ⅰ,J)=KKD (K)
其中:N——环总数;
LOTN(Ⅰ)——第Ⅰ环管段数。
2.3.2 求节点水压时的数据转换
管段ij的水头损失hij与其两端节点i和j的绝对水压Hi、Hj的关系式为:hij=Hi-Hj。有递推式Hj=Hi-hij。定义第Ⅰ环内第J管段的水头损失为H(Ⅰ,J),第K节点水压为HP(K),采用节点-管段转换矩阵KL(Ⅰ,J),则程序为:
HP(1)=H(1,1)
DO 40Ⅰ=1,N
HH=HP(KL(Ⅰ,1))
DO 40 J=2,LOTN(Ⅰ)
K=KL(Ⅰ,J)
HH=HH-H(Ⅰ,J-1)
40 HP(K)=HH
其中:H(1,1)——某一已知水压值;
N—环总数;
LOTN(Ⅰ)——第Ⅰ段管段数。
2.3.3 求初分流量时的数据转换
管段初分流量的表达式为qij=kj-ki[2],式中ki(i=1,2,...,NJ)是节点上数据,它由解线性代数方程得到。仍然采用节点-管段转换矩阵KL(Ⅰ,J)对实现节点数据到管段数据的转换。求qij的程序如下:
DO 30Ⅰ=1,N
DO 30 J=1,LOTN(Ⅰ)
K=KL(Ⅰ,J+l)
KⅠ= KL(Ⅰ,J)
30 Q(Ⅰ,J)=P(K)-P(K1)
式中;Q(Ⅰ,J)——第1环内第J管段流量qij;
P(K)——第k节点系数Kk;
NJ——节点总数;
N——环总数。
4 结语
在实际城市给水管网计算中,应用本文介绍的管网图形的两个基本关系矩阵和数据转换方法,可以大大减少输入数据量,从而为优质快速地完成全部计算提供了有力的支持。
参考文献:
[1]王国明,王毅 给水环网计算程序中的数据转换方法[J].工业 用水与废水,1999,30(4):41-43.
[2] 王国明.环状给水管网的初始流量分配[J].化工给排水设计,1998,(4):1-4
作者简介;王国明(1945-),男,江苏太仓人,副教授,合肥工业大学土木建筑工程学院,电话(0551)2905747。
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 [email protected] ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








