城市需水量灰色预测的探讨

张雅君, 刘全胜
(北京建筑工程学院城市建设工程系，北京100044)

　　摘 要：从灰色模型的特点与需水量本身的变化规律出发，揭示了GM(1,1)模型的应用条件及其在需水量预测中的应用范围，以东京都需水量为例进行了验证，并对北京市需水量进行了灰色预测。?
　　关键词：需水量；灰色模型；预测?
　　中图分类号：TU991.31
　　文献标识码：C
　　文章编号：1000-4602(2002)03-0079-03

　　灰色系统理论认为，尽管客观事物或系统表象复杂、数据离乱，但它总是有整体功能和有序的，具有某种内在规律，关键在于怎样用适当的方法去挖掘和利用它［1］。灰色预测模型(GM)通过对原始数据进行生成处理，使其呈指数趋势变化，建立指数微分方程，最终得到预测模型。?
　　GM的一般表达式为GM(h,n)，即对n个变量用h阶方程表示。基于灰色系统的特点，大多数预测模型采用GM(1,1)及其改进模型。
　　由于初始时序列是否满足非负的齐次指数变化规律是能否用GM建模的关键，因此建模条件应是初始时序列满足指数变化规律。从数学角度看，非负的指数序列实质上就是相对增长率恒定的序列，所以判断一个序列是否适用于GM建模的依据也应从序列的相对增长率入手，基于此提出一种新的相对增长率判定准则。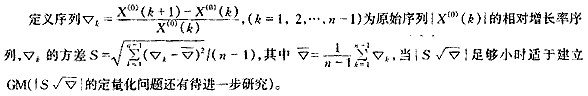 　

1 　理论依据及应用条件

　　灰色模型是一个指数模型，这也就决定了它应该用在按指数变化的系统。所以，探讨一个系统是否可用灰色预测的方法，实质上是讨论该系统是否按指数规律变化(同样可用判定)。?
　　在其他因素不变的条件下，城市需水量增长与人口增长呈线性关系，而人口的增长方式在一定时期内符合指数增长规律^［2］。此外，经济的发展在一定时期内表现为等相对增长率的指数增长规律(如目前我国的经济增长率维持在7%～8%左右)。在不受水资源短缺制约的条件下，经济的增长必然带动需水量的增长。而用水系统本质上并没有一阶正反馈系统特性，需水量增长速率与该时期的用水量并没有逻辑上的关系。但是，基于需水量与人口、经济之间的密切关系，在需水量增长不受水资源约束时，人口、经济的指数增长特性将传递给需水量，此阶段用GM建模可得到较好的预测结果。?
　　因水资源短缺，使得工业和生活用水受到约束，各国政府都采取了节水措施，此时用水量的增长不再随人口、经济等比例增长。一方面经济、人口的增长使需水量呈上升趋势；另一方面由于用水政策、结构调整、工艺改革等诸多原因使需水量出现下降的趋势。所以，此时的用水量呈波动性上升趋势(值偏高)，不宜用GM建模预测。?
　　未来某些国家可能出现人口下降趋势(特别是中国、日本等人口密度高的国家)，而且在以节约资源为特点的可持续发展模式中，产业结构的调整、科技的进步也势必引起需水量的下降。需水量的负增长在这一时期内也以等相对增长率的指数方式减少，因此用GM建模也能得到较好的预测结果。?
　　以日本东京都需水量情况为例，GM模型的应用条件得到了很好的验证。东京都水道局负担23个区及多摩地区的供水，东京都1960年—1999年的人口增长情况如图1所示。其中，20世纪60年代初到70年代中呈现出快速增长的势头，这一时期经济增长率相对较高，人口、经济的指数增长特性传递给需水量，因此它呈现出指数增长趋势，用GM建模可得到较好的预测结果。

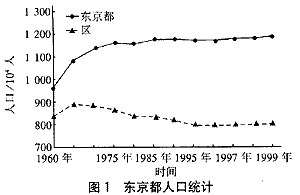
　　以1978年—1986年的用水量数据建立灰色模型，结果见表1。?

表1 东京都1978年—1986年用水量数据拟合结果 年份 实际值(10⁴m³/a) 拟合值(104m3/a) 相对误差(%) 平均相对误差(%) C值 1978 1776 1776.0 0.00 0.90 0.5719 1979 1728 1706.3 1.25 1980 1665 1704.5 -2.37 1981 1694 1702.6 -0.51 1982 1706 1700.8 0.31 1983 1728 1698.9 1.68 1984 1710 1697.1 0.75 1985 1690 1695.3 -0.31 1986 1678 1693.4 -0.92 　注： 实际值＞拟合值时，相对误差为正值；实际值＜拟合值时，相对误差为负值。

　　从表1的C值结果看，也证实了用水量波动上升期间不宜采用GM建模。由人口缓慢增长、传统家庭形式的变迁、经济缓慢增长等现象推测，未来较长时期内东京都需水量增加缓慢，其预测模型如下：

　　

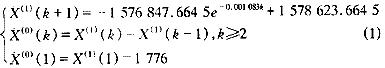
2 　北京市需水量的灰色预测

　　以北京市1989年—1999年的用水量数据(见表2)建立GM模型并进行预测。

表2 北京市用水量数据　10⁴m³/a? 年份 工业用水量 生活用水量 总用水量 1989 454105.3 51428.7 96834 1990 40939.8 52852.8 93792.6 1991 38327 56619.5 94946.5 1992 41575 58376.6 99951.6 1993 38251.7 62571.9 100823.6 1994 41431.2 67295.2 108726.4 1995 39437.3 70540.5 109977.8 1996 39824 69860.5 109684.5 1997 41622.1 75573.5 117195.6 1998 35644.8 78731.9 114376.7 1999 37354.7 82715.5 120070.2

　　工业、生活、总用水量的相对增长率k及其方差S的计算结果如表3所示。

表3 ?k及S计算结果 项目 工业用水量的k 生活用水量的k 总用水量的k 1 -0.098 0.028 -0.031 2 -0.064 0.071 0.012 3 -0.085 0.031 0.053 4 -0.080 0.072 0.009 5 0.083 0.075 0.078 6 -0.048 0.048 0.012 7 0.010 -0.010 -0.003 8 0.045 0.082 0.068 9 -0.145 0.042 -0.024 10 0.048 0.051 0.050 -0.0164 0.0490 0.0224 s 0.0770 0.0266 0.0359 4.70 0.54 1.604

　　工业用水量的GM(1,1)模型如下：

　　

　　生活用水量的GM(1,1)模型如下：

　　

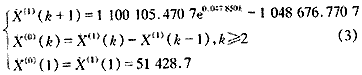
　　总用水量的GM(1,1)模型如下：

　　

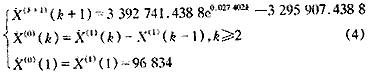
　　拟合及预测结果如表4所示。

表4 数据拟合值及2000年—2002年预测结果 项 目 工业用水量 生活用水量 总用水量 实际值(10⁴m³/a) 拟合值(10⁴m³/a) 相对误差(%) 实际值(10⁴m³/a) 拟合值(104m3/a) 相对误差(%) 实际值(10⁴m³/a) 拟合值(104m3/a) 相对误差(%) 1989年 45405.3 45405.3 0.00 51428.7 51428.7 0.00 96834.0 96834.0 0.00 1990年 40939.8 40746.1 0.47 52852.8 53920.0 -2.02 93792.6 94252.9 -0.49 1991年 38327.0 40450.4 -5.54 56619.5 56562.8 0.10 94946.5 96817.1 -2.03 1992年 41575.0 40156.8 3.41 58376.6 59335.1 -1.64 99951.6 99562.4 0.40 1993年 38251.7 39865.4 -4.22 62571.9 62243.3 0.53 100823.6 102328.4 -1.49 1994年 41431.2 39576.1 4.48 67295.2 65294.1 2.97 108726.4 105171.1 3.27 1995年 39437.3 39288.9 0.38 70540.5 68494.3 2.90 109977.8 108092.9 1.71 1996年 39824.0 39003.7 2.06 69860.5 71851.5 -2.85 109684.5 111095.8 -1.29 1997年 41622.1 38720.7 6.97 75573.5 75373.2 0.27 117195.6 114182.1 2.57 1998年 35644.8 38439.7 -7.84 78731.9 79067.5 -0.43 114376.7 117354.1 -2.80 1999年 37354.7 38160.7 -2.16 82715.5 85942.9 -0.27 120070.2 120614.3 -0.45 2000年 37883.8 87008.2 123965.1 2001年 37608.8 91272.8 127409.0 2002年 37335.9 95746.4 130948.4 平均相对误差（%） 3.412 1.271 1.500 C值 0.5066 0.0602 0.1236

　　由表3、4中数据可见，工业、生活用水量及总用水量中工业用水量的=4.7为最大(C=0.5066)，预测结果不可靠。究其原因，一方面北京市工业产业结构的调整、节水措施的加强使工业用水量呈减少趋势；另一方面工业的高速发展使其用水仍不断增加，因此表现出极强的波动性，不宜用灰色方法预测。生活用水量的=0.54为最小(C=0.0602)，可判定结果可靠。这是由于生活水平的提高、城市人口增长缓慢，生活用水量仍保持较为平稳的指数增长趋势所致。总用水量在工业、生活用水双重因素的影响下表现出一定的波动性，但用GM进行较短周期的预测可得到较好的效果(C=0.1236)，若周期过长则可靠度降低。

3 　结论

　　GM(1,1)模型本身是一个指数模型，其预测效果在很大程度上取决于原始数据的特点。用水量在某些时期内表现出一定的指数变化规律，适用于GM(1,1)模型；而在某些时期则表现出较强的波动性，不宜用GM(1,1)模型。
　　此外，一般按指数规律变化的状态变量的增长常数随时间变化，所以GM(1,1)模型的预测周期不宜太长，否则将带来很大的系统误差。

参考文献：

　　［1］聂相田,邱林,朱普生,等.水资源可持续利用管理不确定性分析方法及应用［M］.郑州:黄河水利出版社，1999.
　　［2］王其藩.系统动力学［M］.北京:清华大学出版社，1988.

---

　　电　　话：(010)68322517(O)?
　　E-mail:[email protected]
　　收稿日期：2001-07-10?
　　修回日期：2001-08-08