一种确定滤池过滤周期的合理方法
唐友尧
摘 要 本文在试验的基础上,建立了滤池过滤水头与出水浊度的数学模式,并求得满足水质要求的最大过滤水头损失值,从而求得过滤周期。
关键词 过滤周期 过滤水头损失 数学模式
0 引 言
滤池的过滤周期是根据最大过滤水头损失或出水水质确定的,当滤池运行达到最大过滤水头损失或出水水质不符合要求时,滤池便停止过滤进行冲洗。出水水质可以根据国家颁布的《生活饮用水卫生标准》来确定,但最大过滤水头损失如何确定呢?国内外很少有人进行研究。《给水排水设计手册》规定冲洗前的水头损失最大值一般采用2.0~2.5m.为什么要定这么大?据笔者了解,还没有这方面的依据,也没有把它与出水水质联系起来,现水厂出水水质标准提高了,浊度由原来的5度降低为3度,最大过滤水头损失是否还有必要采用2.0~2.5m值得探讨。笔者认为,合理的最大过滤水头损失应该是满足水质要求的最大过滤水头损失,采用此过滤水头损失值来确定过滤周期比较合理。它可以通过试验并建立数学模式来求得。
1 试验装置
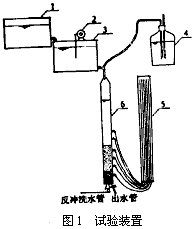 最大过滤水头损失值的确定受许多因素的影响,如滤前水浊度、滤速、滤料的种类、粒径及厚度等,而且某些因素,如滤前水浊度、滤速等在生产滤池上不好控制,故我们采用如图1所示的装置进行试验。该装置主要由滤管6、测压板5、高位水箱1、控制水箱3、定量投药瓶4及循环水泵2等组成。其中滤管直径为10cm,高2.70m。滤料级配为:d10等于0.58mm,d80等于1.16mm,K80等于2;滤料厚度为70cm,承托层采用砾石,厚度为30cm。高位水箱容积为0.24m3,其内装有循环水泵,用于搅拌控制水箱中的原水,以防止沉淀。定量投药瓶容积为10L,所加药剂采用固体碱氯化铝,配制成浓度为1/10000的溶液。
最大过滤水头损失值的确定受许多因素的影响,如滤前水浊度、滤速、滤料的种类、粒径及厚度等,而且某些因素,如滤前水浊度、滤速等在生产滤池上不好控制,故我们采用如图1所示的装置进行试验。该装置主要由滤管6、测压板5、高位水箱1、控制水箱3、定量投药瓶4及循环水泵2等组成。其中滤管直径为10cm,高2.70m。滤料级配为:d10等于0.58mm,d80等于1.16mm,K80等于2;滤料厚度为70cm,承托层采用砾石,厚度为30cm。高位水箱容积为0.24m3,其内装有循环水泵,用于搅拌控制水箱中的原水,以防止沉淀。定量投药瓶容积为10L,所加药剂采用固体碱氯化铝,配制成浓度为1/10000的溶液。
本试验采用直接过滤,滤前水浊度控制在100度左右。原水由高位水箱1流入控制水箱2,再流入滤管6进行过滤,使原水得以净化。清水从滤管底部出水口流出。随着过滤不断进行,滤层杂质逐步堵塞,滤层中的水头损失相应增加。当出水浊度不符合要求时,就停止过滤进行反冲洗。
在运行中,每隔一小时取滤后水样一次,用光电浊度仪测出浊度,同时从测压板上读出滤层水头损失值,并做好记录。对于原水浊度和滤速定期测定,使其保持恒定。
2 试验方法
为了节约试验次数,又找出最佳组合,我们采用正交试验法,即利用正交表来安排试验,并利用它来计算和分析试验结果。根据需要,我们采用三因素二水平的正交试验,以得出一组平均出水浊度最低的最佳组合。经多组试验,现选择有代表性的一组列于表1
 注:①、②为水平代号
注:①、②为水平代号
从表1中可以看出加矾量极差大,故它对出水浊度的影响最大,这在理论上也是解释得通的,因为加矾能改变水中颗粒的性质,使它与滤料容易粘附,故对过滤效果影响很大。从表中还可以看出,三因素都是第二水平的出水浊度最低,故最佳组合为:滤速10m/h,原水浊度100度,加矾量2.0mg/L。用上述最佳组合再做一次试验,其结果填入表2中,并根据结果绘制滤池出水浊度和过滤水头损失与时间的关系曲线(见图2中实线)。
注:原水浊度100度,加矾量2.0mg/L,滤度100m/h
3 数学模式的建立
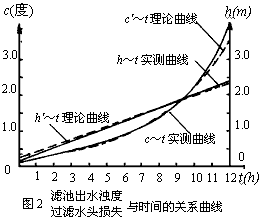
从图2可看出,出水浊度c与时间t的关系为指数关系,过滤水头损失h与时间t的关系为直线关系。先通过回归分析求出c~t和h~t的关系式,然后在此基础上求出过滤水头损失h与出水浊度c的关系式;
2.1 c~t的关系式
对于c~t的关系曲线,令其方程为
c=aebt (1)
式中a、b可用下述回归分析法求得。
将式(1)变换为
c/a=ebt (2)
取对数
lnc-lna=bt
即 Inc=Ina+bt (2)
令 y1=Inc Xi=t M=Ina
式(2)可写成
yi=M+bXi (3)
令 ![]()
要使Q达到最小值,只需在式(4)中分别对M、b求偏导,令它们等于0,于是M、b满足
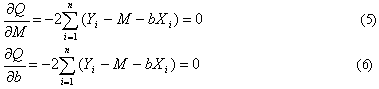
从式(5)得
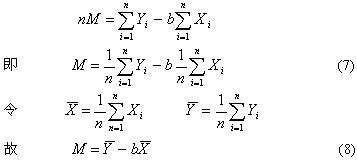
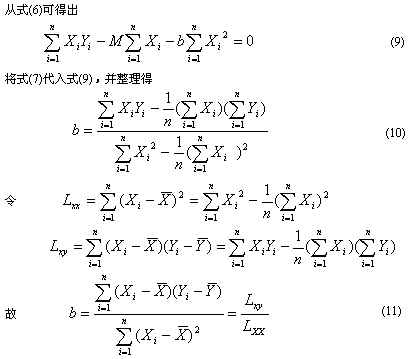
按表2中的t和C值列出回归分析计算表3,从表3中可以算得如下结果:
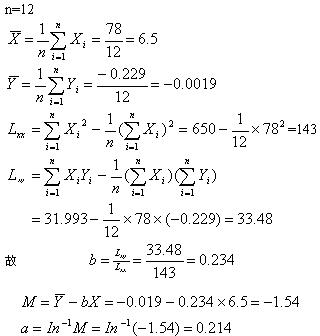
将a、b值代入(1)得过滤出水浊度与时间的关系式
Ct=0.214e0.234t (12)
根据式(12),算出不同t的Ct值(见表4),并绘制Ct~t关系曲线(见图2中的虚线),与实测c~t关系曲线比较,可以看出, Ct~t曲线与c~t曲线比较接近,故式(12)较正确地反映了c与t之间的关系。
2.2 h ~ t的关系式
因h与t的关系为直线关系,故令该方程为
h=a+bt (13)
按表1中的t、h值,同样通过回归分析法可求得
b=0.18 a=0.18
将a、b值代入式(13)得
ht=0.18+0.18t (14)
根据式(14)算出不同t的 值(见表4),并绘制 ~t关系曲线(见图2中的虚线),与实测h~t关系曲线比较,可见两条直线比较接近,说明式(14)较正确地反映了h与t之间的关系。
2.3 h~c关系式
 由式(14)得
由式(14)得
t=(ht-0.18)/0.18 (15)
将式(12)做以下变换
c/0.214=e0.234t
取对数
lnc-ln0.214=0.234t (16)
将式(15)代入式(16),并整理得过滤水头损失与出水浊度的数学模式
ht=0.77lnC+1.37 (17)
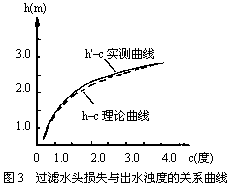
根据式(17),算出不同C下的ht值(见表5),并绘制ht~c关系曲线(见图3中虚线),同时根据表2中数据绘制h~c关系曲线(见图3中实线),可以看出,这两条直线是比较接近的,说明式(17)较正确地反映了h与c之间的关系。
4 最大过滤水头损失值与过滤周期的求解
为了保证水厂出水浊度不超过3度,一般滤池出水浊度应在3度以内。在此,我们取滤池出水浊度等于2度作为求最大过滤水头损失值和过滤周期的先决条件。
在方程ht=0.77lnC+1.37 中,取c=2代入,求得t=9.28h 。然后将它代入方程ht=0.18+0.18t,求得t=9.28h。这就是通过试验后求得的最大过滤水头损失值和过滤周期。
综上所述,在保证出水浊度为2度的情况下,滤池最大过滤水头损失值取1.8~1.9m,过滤周期取9~10h比较合理。
5 结 论
5.1本文为滤池过滤周期的确定提供了一种方法,因本文通过测试建立了过滤水头损失与出水浊度的数学模式,并能很方便地根据所要求的出水浊度确定出滤池最大过滤水头损失值,从而求得过滤周期。
5.2用文本方法确定滤池过滤周期比较合理,一方面能保滤池出水水质,另一方面能使过渡水头得到合理利用。
5.3应当指出的是过滤周期的合理确定是因条件而异的,因过滤周期与滤前水质、滤层组成、滤速及所用药剂等因素有关,因此应通过试验来确定。
⊙作者通讯处:430074 华中科技大学环境科学与工程学院
电 话:(027)87808129
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 [email protected] ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








