遗传算法在供水系统优化调度中的应用

田一梅，李江涛，戴雄奇，李鸿
(天津大学环境工程系，天津300072)

　　摘　要：对遗传算法应用于求解供水系统的优化调度问题进行了探讨，并提出了对连续/离散混合变量的编码方法。给出了一个遗传算法应用在优化调度方面的实例，结果表明该算法具有很强的适应性，可实际应用于在线优化调度。
　　关键词：遗传算法；供水管网；优化调度
　　中图分类号：TU991.56
　　文献标识码：C
　　文章编号：1000-4602(2001)12-0063-03

　　城市供水管网系统的优化调度是根据管网实时运行状态确定今后一个调度期中水泵的运行状况，在保证供水服务质量的前提下，使供水系统获得最佳效益。通常可以采用两种方法求解，即直接优化和两级优化，前者以泵站内各种泵的开机台数和流量为变量直接确定优化调度方案；后者则分为两级求解，在确定各水厂最佳供水量、供水压力的基础上，给出各泵站水泵的最佳开机方案。因此，供水系统优化调度的核心就是求解一个多目标优化问题，而选择一种适当的解法就成为问题的关键。由于供水系统优化调度的目标函数及约束条件都是非线性的，虽然可将目标函数分段线性化并用线性优化方法对其求解，但求得的结果难以令人满意。而直接采用非线性优化方法一般又很难保证求得全局最优解，特别是在直接优化调度中由于存在连续/离散混合变量，且当变量多、约束条件复杂苛刻时往往只能求出局部最优解，要想取得全局最优解则需不断改变初始点，在多个局部最优解中择其最优，显然这难于满足在线优化调度的要求。而两级优化调度由于将问题分解，变量少且单一，约束条件宽松，故求解容易。但有些供水系统因泵站内恒速泵种类较少，又没有设置调速泵，因此很难确定出满足第一级优化要求的泵站开机方案，故不适于采用两级优化调度。由此可见，寻求更好的优化算法是供水系统优化调度中的一个关键问题。

1　直接优化调度数学模型

　　直接优化调度是以各泵站投入运行的水泵单机流量和开机台数为变量，将水源、水泵及管网作为一个有机整体来建立模型。由于供水系统中各水源的供水能力、供水成本不同以及投入运行的水泵组合方式不同，必然存在着多种不同的供水方案可满足要求，因此就存在着如何经济、合理地调整各水厂、水泵之间的相对关系，既使节点能量浪费最小、压力分布均匀，又使经济效益最佳以达到系统整体最优的问题。
　　直接优化调度问题的数学模型表达如下：
　　目标函数

　　　　　

　　　　　

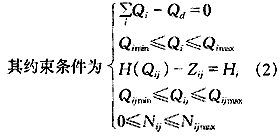
　　式中f1——管网各压力监测点供水压力与该点所需压力之差的平方和
　　　　f2——供水系统的净收益，即供水收益与制水成本、送水电费之差
　　　　 r——换算系数
　 Hk、Hkf——分别为管网宏观模型所确定的监测点k的压力和该点所需的最小压力
　S1i、S2i——分别为水厂i的供水水价和单位制水成本
　S3i、σi——分别为水厂i的基本电价和耗电电价
　Nij、Nijmax——分别为水厂i中水泵j投入运行的台数和可开机台数
　Qi、Qimin、Qimax——水厂i的供水量及供水量范围
　Qij、Qijmin、Qijmax——分别为水厂i中水泵j的供水量和该泵高效段流量
　H(Qij)、η(Qij)——分别为水厂i、水泵j在流量为Qij时的供水扬程和供水效率
　　　　　δij——水厂i、水泵j的机电传动效率
　　　　　Zij——水厂i、水泵j的吸水扬程与压力表前水头损失之和

2　用遗传算法求解

　　某城市供水系统有2个水厂、7个管网压力监测点，管网中最不利点的压力按200 kPa计算。该市用水量约35×10⁴m³/d，各水厂供水量和水泵参数见表1。

表1　各水厂供水量和水泵参数 项目 水厂一 水厂二 水泵型号 14SA—10B 12SH—9 12SH—9A 16SA—9C 14SA—10B 水泵可开机台数 5 2 2 4 3 水泵高效段流量(L/s) 350～250 270～160 248～147 350～250 350～250 水厂供水量范围(L/s) 1 750～0 3 486～0

　　遗传算法求解直接优化调度问题过程如下：
2.1　编码
　　遗传算法的工作对象是染色体字符串，首先对染色体进行编码。由于水泵台数是离散变量，可直接采用二进制编码；而单泵流量属连续变量，需经离散化处理后再采用二进制编码。为使水泵台数在给定的范围内，作者定义了一套编码规则列于表2。

表2　编码规则 十进制数 1 2 3 4 5 6 7 拆分 1 1+1 3 3+1 3+1+1 3+1+1+1 7 二进制数 1 1,1 11 11,1 11,1,1 11,1,1, 111 二进制位数 1 1+1 2 2+1 2+1+1 2+1+1+1 3

　　表1中5种型号水泵可开机台数分别为：5、2、2、4、3，故由表2可知，染色体上代表水泵台数的基因位数为：4+2+2+3+2=13位。
　　对于连续变量，根据单泵流量(Qij)的范围［0，350］和水泵的特性并兼顾问题求解的难易程度，取单泵流量离散化后的精度为0.68，故由二进制编码精度公式可计算出用9位二进制表示每一个单泵流量，所以染色体上代表单泵流量的基因位数为45位。
　　水泵台数的基因位数与单泵流量的基因位数之和即为染色体总长度：13+45=58位。
2.2　构造适应度函数
　　对于所求的有约束最小化问题，可采用序列无约束优化法的外罚函数将其转为无约束优化问题，同时按照遗传算法的要求将极小值问题转化为极大值问题求解，并保证适应度函数始终为正值。故先将上述有约束非线性优化调度问题式(1)、(2)整理为标准的非线性规划形式：

　　　

　　　

　　再将一个大数(常数C)与目标函数之差作为适应度函数，即：

　　　　max［C-P(X,M)］　　　　(5)
2.3　求解及结果分析
　　根据上述分析编制和调试了遗传算法求解优化调度问题的有关程序，并对上述实例进行计算，主要计算步骤如下：
　　①随机建立由字符串(即二进制代码串表示的水泵开机台数和单泵流量)组成的初始群体；
　　②计算各个体的适应度max［C-P(X，M)］；
　　③根据遗传概率，利用复制、交换、突变产生新群体；
　　④反复执行②、③后，一旦达到终止条件，直接输出最优解(见表3)。

表3　优化调度最优解 　 一厂 二厂 监测点 所需压力(kPa) 优化计算压力(kPa) 水泵型号 14SA—10B 12SH—9 12SH—9A 16SA—9C 14SA—10B 1 314.5 306.2 开机台数 4(11，0，1) 1(0，1) 2(1，1) 0(0，0) 1(01) 2 297.4 293.2 单泵流量(L/s) 350(111111111) 172(11111011) 133(11000010) 0(000000000) 285(110100000) 3 218.8 215.1 水厂供水量(L/s) 1400 723 4 208.4 205.2 所需供水压力(kPa) 403.4 473.8 5 319.8 317.8 优化计算压(kPa) 415.8 452.9 6 401.3 396.7 管网需水量(L/s) 2 149 管网供水量 2 123 供需水量差 -26 7 356.5 353.1 注：括号内为解变量的二进制代码。

结果分析：
　　①将最优解代入优化调度原问题式(1)、(2)，满足原问题的要求，证明用遗传算法求解连续/离散混合变量问题是行之有效的。
　　②遗传算法适用面宽，对问题要求很少，如对目标函数只要求有定义，不要求其连续、可微，对约束条件也无任何限制；而采用传统的数学规划方法，当约束条件比较苛刻时进入可行域比较困难。故该算法能够克服传统优化方法的一些弱点，可以解决许多传统方法不能解决的问题。
　　③遗传算法在整个解的空间内搜索，具有较大的把握求得全局最优解。
　　④遗传算法计算时间较短(仅需2～3 min)，满足在线调度要求。

3 结语

　　综上所述，用遗传算法求解输配水系统优化调度问题得到的结果是令人满意的，这说明遗传算法是一种比较好的搜索算法，它不仅快速、准确、搜索遍及全空间，具有较大的把握得到全局最优点，而且不用对原问题作过多的分析处理，具有很高的适应性和很强的鲁棒性。当然遗传算法也存在一些缺点，如遗传算法的操作参数和优化结果相互之间比较独立，故对于操作参数的选取比较困难；此外由于遗传算法还处于发展的初级阶段，尚有许多问题需要研究和探讨，比如对于大型复杂问题的收敛速度还比较慢等。对于上述问题，前者可通过使用者编程以自动寻求不同问题的最佳操作参数；后者则有待于该算法的不断改进和进一步
完善。

参考文献：

　　［1］赵新华.城市配水系统优化运行的研究［J］.中国给水排水，1992，8(3)：18-22.
　　［2］王平洋.加快遗传模糊算法的搜索过程［J］.电网技术，1999，23(5)：3-10.
　　［3］周明，孙树栋.遗传算法原理及应用［M］.北京：国防工业出版社，1999.

---

　　电 话：(022)27400830
　　收稿日期：2001-06-15