混凝控制中的数学模型及其应用

黄兴德，于萍，罗运柏
（武汉大学化学与分子科学学院，湖北 武汉 430072）

　　摘要：水处理中混凝剂加注量的自动控制是一个既重要又难于解决的问题。本文系统介绍了三种典型的数学模型，探讨了它们对于混凝控制技术的促进作用，分析了基于不同数学模型的控制技术间的差异。
　　关键词：水处理；数学模型；混凝；模糊控制
　　中图分类号：TU991.22
　　文献标识码：A
　　文章编号：1009-2455(2001)04-0004-04

Mathematical Models in Cogulation Control and Their Application
HUANG Xing-de，YU Ping，LUO Yun-bai
(College of Chemistry and Molecule，Wuhan University，Wuhan 430072，China)

　　Abstract:The automatic control of coagulant dosing is important and yet difficult to resolve．Three typical math-ematical models are systematically introduced in this paper，with their impulses to the development of coagulation control techniologues probed abd the differences among the controlling technologies based on different mathematical models analyzed．
　　Key word_s:water treatment；mathematical model；coagulation；fuzzy control

　　混凝工艺是传统水质净化工艺中较为重要的环节，准确控制加药量是取得良好混凝效果的首要前提。混凝剂加注量的自动控制是一个难于解决的问题，因它不仅与水质参数和水量参数有关，还与净水构筑物的性能和混凝剂自身效能等因素有关^[1]。尽管如此，建立于经典控制、现代控制和智能控制理论上的各种控制策略应用于混凝过程的控制个案十分丰富。本文结合一些较成功的应用范例探讨数学建模技术在混凝控制中的作用。

1 基于多变量参数模型的混凝控制技术与实例^[1-2]

　　多变量参数模型是以若干原水水质、水量参数为变量，建立变量与加药量之间的函数表达式。首先，进行模型结构和参数的选取。模型结构有线性、非线性等形式，参数的选取往往依赖大量验前知识，运用数学统计检验出具有可测性的主要影响因素。其次，确定模型中各项系数，由多年的运行资料进行统计分析予以确定。以应用于上海石化总厂水厂的模型为例，以原水浊度、温度（t＞21℃），pH、流量作为自变量：
　　K=291.5+0.2217X₁+9.9688X₂+37.9375X₃+0.5886X₄-2.648×10^-4e^(X₂-21)-1.5388×10^-3X₁²-1.2520X₂X₃
　　式中：K－前馈药量，kg/km³；
　　　　　X₁－原水浊度，mg/L；
　　　　　X₂－原水温度，℃；
　　　　　X₃－原水pH值；
　　　　　X₄－原水流量，m³/h。
　　计算机系统自动采集参数数据，并根据模型自动控制加注量。此模型属于前馈模型，只能用于开环控制。为提高控制精度，稳定出水水质，须进一步建立一个以沉淀水浊度（控制目标为5度）作为反馈修正模型：

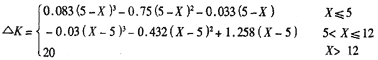
　　式中：△K－反馈微调药量，kg/km³
　　　　　X－沉淀水浊度，mg/L
　　多变量参数模型基础上的前馈－反馈复合混凝控制系统，能迅速响应原水水质及水量参数变化，但系统的运行依赖于每一块仪表准确可靠的工作，其控制系统框图如图1：

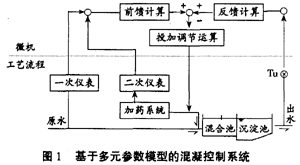
　　其中：一次仪表包括用于原水水质分析的浊度计、酸度计、温度计和原水流量计，二次仪表包括用于加药系统的液位汁、密度计、药管压力表和流量计，Tu为沉淀水浊度计。

2 基于特性参数模型的混凝控制技术^[2-5]

　　基于特性参数模型的混凝控制系统见图2。

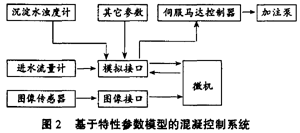
　　随着人们对混凝机理研究的深入，寻求表征混凝效果的特性参数及其数学物理模型，从而建立简单实用的单因子混凝控制系统成为可能。这类模型皆以混凝过程中某种微观特性的变化作为加注量确定的依据。比较典型的有以流动电流作为特性参数的SCD法，以透光脉动值作为特性参数的透光脉动法等。这里介绍一种以絮体等效直径作为特性参数的模型。
　　絮体的沉降规律比较复杂，常简化用颗粒沉降的Stockes公式描述：

　　式中：υ－絮体沉降速度，cm/s；
　　　　　ρs－絮体体积质量，g/cm³；
　　　　　ρ－水的体积质量，g/cm³；
　　　　　d_s－絮体直径，cm；
　　　　　μ－水的粘滞系数，g/(cm·s)。
　　随着絮体粒径的变化，絮体体积质量遵循下式的规律变化：
　　ρs-ρ=d_s^-Kp （2）
　　式中：
　　Kρ－系数；1.2～1.5，决定于混凝剂加注率与原水水质
　　综合（1）、（2）式得出絮体粒径与沉淀速度的关系式：

　　上述分析均假设絮体为球状颗粒，而实际絮体是不规则的，其大小、形状通过一个传感器采集的絮体图像反映出来。二维的絮体图像可以用四个参数刻画其特性：表示絮体大小的絮体面积S；与形状有关的絮体周长l；与松散程度有关的絮体中间空出面积S₀；絮体的长宽比m₀利用下面的公式换算成一个参量“等效直径”φ：

　　式中：
　　k₁、k₂、k₃－周长、长宽比、中空面积的折扣系数，为0－1的小数
　　由（3）、（4）式可知，等效直径越大，沉降速度越快，即絮体形成得越好，沉淀越充分，沉淀水的浊度也就越小。
　　但是，参量φ中仍无法表征混凝的整体效果。实际使用的传感器取景窗水域面积为26mm×20mm，取景厚度约3.5mm，该截面一般包含近百个絮体。设定系数每5s采集一幅图像，按（4）式计算每个絮体的等效直径，每5min即可得60幅图像中所有絮体等效直径及其数值分布情况，在此基础上适时计算平均等效直径：

　　φ=∑(niφ_i)/∑n_i　　　　　　　　　　　　　(5)

　　式中：φ_i－第i个絮体的等效直径，m；
　　　　　n_i－等效直径为φ_i的絮体个数。
　　通过实验表明，在沉淀条件相对稳定的情况下，平均等效直径与沉淀水浊度有很好的相关性。至此，找到作为控制目标的特性参数及其模型。加注率等于平均等效直径的实测值与设定值之差，通过PID运算得到。

3 基于模糊逻辑模型的控制技术及其设计^[6-8]

　　基于模糊逻辑、神经网络等智能控制方法为解决混凝剂加注量控制开辟了一条新的途径，此类控制方法的最大特点就是具有仿人的功能（学习、推理）。
　　图3为模糊逻辑理论应用于絮凝剂加注量控制的系统框图。S为沉淀水浊度的目标值，E、CE、U为e、ce、u对应的模糊量。Ke和Kce分别为浊度偏差e、浊度偏差变化ce的量化因子，Ku为输出比例因子，Ke、Kce、Ku由e、ce、u的基本论域和规格化论域确定。模糊控制的核心是模糊控制器，从图3知它由三部分组成：模糊化层、模糊推理层、解模糊层。下面介绍利用Matlab，环境下模糊逻辑工具箱设计应用于混凝控制的模糊控制器：

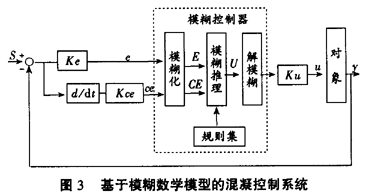
　　①模糊控制器的结构选择二维输入，单维输出结构模式：以浊度偏差e（取一段时间内沉淀水浊度的平均滤波值与目标值S之差）和浊度偏差的变化率ce（取相同一段时间内浊度偏差变化的微分值）作为输入，加药量的变化量U作为输出控制变量。
　　②精确量的模糊化。模糊控制器是利用一定语言控制规则进行工作的，因而输入输出是以自然语言形式给出的变量。根据精度的需要，本模糊控制器中e和u的语言模糊集为（NB，NS，O，PS，PB），ce的语言模糊集为（NB，O，PB），完成对输入输出空间的模糊分割。根据综合试验和实际运行数据，确定e的基本论域为[-5，45]，ce的基本论域为[-40，40]，输出变量u的基本论域为[-60，60]。对e、ce、u基本论域的量化档次n均取n＝5，将连续确定量e、ce、u离散化为在[-5，5]上变化的整型变量，区间[－5，5]上的离散整数称为模糊变量的规格化论域。本设计中语言变量的隶属函数选择为三角形，其参数和图形直接从工具箱中定义。输人输出变量的模糊子集、论域、隶属函数确定后，确定规模化论域内元素对模糊语言变量的隶属度，并据此建立语言变量E、CE、U的赋值表。
　　③控制规则集R的建立。规则集R是在大量历史数据和操作者的经验基础上，操作人员的一条控制策略对应一条模糊条件语句：
　　IF E=PB，THEN U=PB；
　　IF E=PS and CE=PB，THEN U=PB；……
　　IF－THEN语句的前件代表了本课题中的现象，后件则表示控制行为。根据手动控制策略，整个控制规则所对应的总模糊关系为R=∨R_i，总结、合并本课题的所有控制规则约为十条。模糊控制规则要求同时进行完备性、一致性和交互性检验，其基本原则是：适当考虑偏差变化模糊量CE大小的前提下，当浊度偏差较大时，以尽快消除偏差为主选择控制变量；当偏差较小时，注意防止超调和保证被控系统的稳定性来选择控制变量。
　　④输出信息的模糊判决，并完成由模糊量到精确量的转化。由模糊控制原理可知，模糊控制器的输出是一个模糊集合，它反映控制语言的不同取值的一种组合，为充分利用输出模糊集合所包含的信息，从工具箱中定义标准解模糊方法，如重心法、最大隶属度法等。计算得到的模糊控制输出量U乘以输出比例因子Ku即为精确控制量u，它就是实际加到被控制过程上的控制变化量。
　　⑤由于浊度可连续测定，系统采样周期取5－30s。本设计在离线计算的基础上，可以获得一个混凝模糊控制查询表，用于适时控制。

4 问题与讨论

　　①基于受控对象的数学建模技术主要有两种：一是机理演绎法，二是实验辩识法。多元参数模型即是通过实验辩识法建立的，建立步骤包括过程辩识。参数估计两步。由于混凝过程内在机理比较复杂，特性参数模型建立必须结合上述两种方法，首先利用机理演绎法寻求恰当的特性参数，然后在实验辩识法的基础上建立系统的输入、输出函数关系。基于多元参数模型和特性参数模型的混凝控制技术均属于传统控制，依赖于过程模型。基于模糊数学模型的混凝控制属于智能控制，通过模仿人的思维方式和人的控制经验来实现的一种控制，它不要求建立过程的精确数学模型。
　　②多元参数模型、模糊数学模型均不体现药耗的本质，特性参数模型是建立在混凝机理上，反映过程的微观本质，其与PID的控制结合，衍生出不同控制方案，实际应用最为广泛，关键在于寻找一个滞后时间短、与沉淀水浊度具有相关性且易于检测的特性参数。从理论上讲，多元参数模型控制作用最好，但模型的精度和可靠性难以保证。模糊控制过程的动态响应优于特性参数模型的PID控制，并对过程参数的变化具有较强的适应性。
　　③多种控制策略、数学模型的成功结合应具有正确的一致性。上述三种模型基础上的混凝控制技术都体现了降低药耗、稳定水质、降低劳动强度、提高管理水平的目的。

参考文献：
　　[1]崔福义，袁永臻．给水排水工程仪表与控制[M]．北京：中国建筑工业出版社，1999．
　　[2]钟淳昌，朱方达，等．数学模型加矾自动化技术[J]．中国给水排水，1989，(5)：20～24．
　　[3]宋启敏，陆敏刚，义泳，等．混凝剂加注量的自动控制的新方法[J]．中国给水排水，1999，15(4)：1－4．
　　[4]杨凯人．显示式絮凝控制系统（FCD）在水厂的应用[J]．中国给水排水，2000，16(3)：41－43．
　　[5]Kenichi Kurotfanim，et al．Advanced control of coagulation process applying floc sensor．In:IWSA．Specialized Conference on Advanced Treatment and Intergrated Water System Management into the 21st Century [C]．1995．
　　[6]肖军．模糊控制在自来水厂中的应用[J]．自动化与仪表，1999，14(5)：25～26．
　　[7]章卫国．等．先进控制理论与方法导论[M]．西安：西北工业大学出版社，2000．

作者简介：
　　黄兴德（1975－），男，1996年毕业于武汉水利电力大学化学与环境工程系，现为武汉大学化学与分子科学学院应用化学专业硕士研究生。