城市给水管网优化设计方法与发展
信昆仑 刘遂庆
(同济大学环境科学与工程学院)
摘要 本文简要介绍了给水管网工程领域研究者所使用的传统优化设计方法和最新发展,并对各种方法进行了简单的比较,同时概要介绍了管网可靠度问题在模型中的实现。
关键词 给水管网 优化设计 线性规划 非线性规划 可靠度
1 概述
自本世纪60年代提出给水管网设计优化计算方法以来,研究者在这一领域已经取得了长足的进展,提出和发展了基于最优化理论和管网水力特性的各种设计理论和方法。
最早给水管网设计模型是基于树状管网提出的(例如,kormeli et al(1968),schaake and lai (1969)),这些模型可以寻求全局最优解,然而由于其仅仅适用树状管网,因而对于在实际城市给水管网的设计者来说并无太大的价值。
2 线性规划法
Alperovits and Shamir 于1977年提出所谓线性规划梯度法,并给出了其在复杂管网系统以及多水力工况下的应用,也为以后研究者指出了一条逐步迭代逼近寻优的设计思路,奠定了两阶段法的基础。以管网中无其他组件且是单一工况这一最简单的情况为例:
对于已知的管网分布,预分配管网各管段的流量,对于管网中的各条管段,分别使其有连续几段标准管径的管段组成,各段长度记为Li,j (连接i ,j 节点管段中第m档管径的管段长度) ,构造以下经过简化后的目标函数
![]()
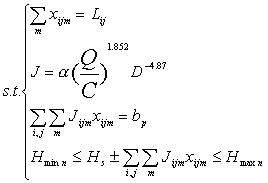 (1)
(1)
说明: Jijm:组成管段Li,j 的第m档管段的水力坡度:
bp: 对于环路为0,对于已知端点水头的路径为两端点的水头差值
Hmaxn,Hminn分别是n节点所允许的最大最小水头值
用经典的线性规划方法容易求出该L.P.问题的最优解,至此完成两阶段法的第一阶段。
第二阶段是:计算目标值关于流量分配的梯度向量:
![]() (2)
(2)
构造第二阶段目标函数
![]() (3)
(3)
该步骤中β的寻找是通过试算实现,即给定初始β值作为相对于最大梯度向量分量的Q值的增量并依次按Gp的比例计算对应Qp的增量,通过试算确定满足该目标函数的β值,从而获得该种管径组合下的最优流量分配,重新回到第一阶段,重新计算该流量分配下的管径组合方案,如此往复直至目标值不再减少为止。
此后,Quindry 等(1981)提出与之相似的算法,不同的是其在第二阶段通过调整节点水头而不是流量分布逼近最优解。Okitsugu Fujiwara 和Do Ba Khang 于1990年提出综合两者交替固定流量分配和节点水头逼近最优解,这些方法都是基于Xi,j为决策变量的线性规划问题,并都对多工况,有泵站,水池及阀门的复杂管网系统进行了讨论。
线性规划方法是对于可行域内最优解的线性逼近,由于管网系统的优化结果倾向于管网树状化,加入最小管径约束只能保证管网的环状,并不能实现真正意义上的管网可靠性问题,因而如何在线性模型中实现可靠度的思想日益为研究者所关注。但是,由于可靠性的度量到目前为止还没有公认的定义,因而所有关于可靠度的线性规划模型问题并不具备统一的形式,也没有广泛的适用性,近几年各国学者分别提出各自关于可靠度的模型,例如, Ian C.Goulter and Francois Bouchart 于1989 年提出的以下模型:
以rij表示单位长度的第i管段第j档管径的管段每年平均的破坏次数,加入以下约束:
![]() (4)
(4)
其中
![]() (5)
(5)
RHSi表示rij服从一定概率分布前提下给定时间内i 管段所允许的故障次数。
Kofiawumah,Ian Goulter 等于1991年提出以熵作为管网可靠度的代用度量:
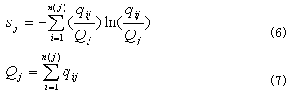
其中qij表示由第i点流入第j点的流量。
此外,Okitsugu Fujiwara等以事故时流量亏值与总需水量的比值、Heekyung Park(1993)以冗余度(redundancy)作为可靠度的度量等等不一而足。总之,可靠度由于其复杂的概念内涵(与管径,管材,阀门的多少,管网的构成,故障的隔离与修复时间有关),因而现有的各种度量方式都不能涵盖所有方面,考虑的越全面,受计算时间及计算速度的影响随管网规模的递增就越明显。
3 非线性规划方法
由于管网优化设计计算问题本身具有的非线性性质,因而也可直接采用非线性规划法解决,对于有泵站情况,经简化后的数学模型可写为:
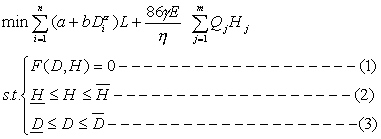 (8)
(8)
n-管段数;m-水源泵站数;a,b,α-管段造价公式系数;E-电费换算系数;γ-能量不均匀系数;η-泵站总效率;Li-管段长度;Qi-节点流量;Hi-节点水头 H,D-节点水头,管径上限;F(D,H)=0-节点连续性方程。
由hazon-willianm公式![]() ,Hi可以表示为Di的非线性函数。于是上述问题转化为以D为决策变量的非线性规划问题,然而对于复杂系统F(D,H)=0将分解为相当庞大的约束集合,增加了用非线性规划法求解的难度。目前,大多数学者倾向于采用独立的水力计算程序求解该约束,这样会大大削减主干问题的约束个数,利于非线性规划方法的求解。具体到非线性规划算法,应用最广泛的是广义简约梯度法(General Reduced Gradient),其中以Lasdon和Waren于1983年开发的GRG2程序最为常用。水力计算程序使用最多的是Wood于1980年开发的KYPIPE(University of Kentucky Model)。
,Hi可以表示为Di的非线性函数。于是上述问题转化为以D为决策变量的非线性规划问题,然而对于复杂系统F(D,H)=0将分解为相当庞大的约束集合,增加了用非线性规划法求解的难度。目前,大多数学者倾向于采用独立的水力计算程序求解该约束,这样会大大削减主干问题的约束个数,利于非线性规划方法的求解。具体到非线性规划算法,应用最广泛的是广义简约梯度法(General Reduced Gradient),其中以Lasdon和Waren于1983年开发的GRG2程序最为常用。水力计算程序使用最多的是Wood于1980年开发的KYPIPE(University of Kentucky Model)。
对于模型中的约束(2),Lansey和Mays(1989,1992)、Ning Duan(1990)等采用了增广拉格朗日乘子的处理方法。
设:![]() (9)
(9)
目标函数改写为:
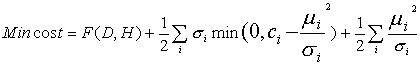 (10)
(10)
其中:ci=min(ci-ci),ci=Hi-Hi,Ci=Hi-Hi
μi—惩罚因子,σi —拉格朗日乘子。
此时该目标函数所对应的约束只有(3),大大减少了问题的规模.同样,如果将管网可靠度看作H,D的函数,模型中可加入以下可靠度约束:
R(H,D)≤R(H,D)≤R(H,D) (11)
该约束的求解也多采用独立子程序计算并以拉格朗日乘子的形式加入目标函数中以降低非线性规划问题的复杂程度,三者的关系可以下图表示:
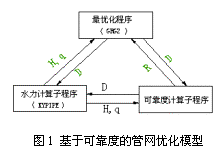
大量的研究者采用了GRG2、KYPIPE两个子程序分别处理最优化部分和水力计算部分,因此各种非线性算法的主要分歧仍然落在可靠度计算子程序上.不同研究者分别采用了不同的度量方式 (最小切割集法,Su Yuchun,1988;RAPS程序,Ning Duan,Lansey,Mays,1990;时间比例法,Cullinane,Lansey,Mays,1992),类似于线性规划方法,不同算法在或是计算时间或是概念涵盖方面都有各自的缺点或长处而分别适用于解决某一特定类型的问题。
4 生物进化规划及遗传算法
近年来,随着生物工程的蓬勃发展,随之而起的遗传学算法开始介入各个工程领域,该算法在有泵管网,管网扩建与改建等课题中也开始有应用(David.E.Goldberg,1987;Simpson 等,1995)。遗传算法(Genetic Algorithm)应用于给水管网优化设计课题中,实质上是一种策略枚举法,以单工况,单水源的简单情况为例:
首先对工程实际所限定的各档标准管径进行编码,于是管网不同的管径组合方案可以形成不同的代码串,经过对每一代码串的解码,由水力计算子程序可以求出该方案下管网的水力特性如H,Q等,进而可以求算用于评价方案优劣程度的目标函数值。然后遗传算法根据生物遗传进化的原理,对产生的初始方案进行选择、重组、变异, 产生新一代个体,仿照生物进化过程代代进化下去,最终可以得到满足要求的最优个体,解码后即为该课题的最优方案。
相对于传统的线性,非线性规划算法,遗传算法的优势在于:(1)算法思路简单,不受规划问题要求的可微、可导、连续等限制,不但可以避免线性规划解的”瓶颈”问题,也避免了非线性规划最后对连续管径进行”圆整”带来的麻烦与偏差(2)由于遗传算法从一组方案出发,扩大了搜索寻优的范围,减少了传统规划方法线式寻优(如按梯度搜索)产生局部最优解与全局最优解差距较大的风险。遗传算法的不足之处在于耗机时太多,对大型复杂管网更是如此.这主要由于其中的选择,交换,变异等过程还没有一个适合管网优化问题的完善算法,同时也是因为该算法贯串了几率的思想而不似传统方法具有确定性。
5.结语
随着研究者在这一领域的不懈努力,给水管网优化设计计算的方法日趋丰富,涉及的问题的深度与广度也日趋加强,具体地说,如何对复杂管网在多种工况时,考虑管网的可靠性情况下,利用原有的线性的或者非线性的方法,或者采用遗传算法之类的新方法进行优化设计,使之更接近城市供水管网的工程实际,并进一步开发相应的软件,是研究者所关注的课题。
参考文献:
[1].I.C.Goulter(1990),”Systems Analysis in Water-distribution network design:From Theory to Practice”,J. Water.Res.Plan.Magmt,vol.118(3),238-248
[2].Alperovits E.,Shamir U.(1977)”Design of optimal water distribution systems”,Water.Resoures.Research, vol.13(6),885-900
[3].Okitsugu Fujiwara,Do Ba Khang(1990),”a two phase decomposition method for optimal design of looped water distribution networks”,Water Resources.Research,vol.26(4),539-549
[4].Ian C. Goulter,Francois Bouchart(1990),”reliability-constrained pipe network model”,J.Hyr.Eng.ASCE, vol. 116(2),211-229
[5]Kofi Awumah,Ian Goulter ,Suresh K Bhah(1991),”entrophy-based redundancy measures in water-distri- bution networks”, J.Hyr.Eng. ASCE,vol..117(5),595-613
[6]Okitsugu Fujiwara,Amal U. Silva(1990),”algorithm for reliability-based optimal design of water networks”, J.Env.Eng.ASCE.,vol .116(3),575-587
[7]Heekyung Part,Jon C. Liebman(1993),”redundancy-constrained minimum-cost design of water-distribution nets”,J.Water.Res.Plan.Magmt.ASCE,vol.119(1),83-99
[8].Kevin E.Laney,Larry W.Mays(1989),”optimization model for water distribution system design”, J.Hyr.Eng., vol.115(10),1401-1419
[9]Yuchun Su,Larry W. Mays,Ning Duan,Kevin E. Lansey(1988),”reliability-based optimization model for water-distribution systems”,J.Hyr.Eng.,vol.114(2),1539-1555
[10].Ning Duan,Larry W. Mays,Kevin E. Lansey(1990), “optimal reliability-based design of pumping and distribution systems”,J.Hyr.Eng.,vol.116(2),249-268
[11].Simpson,Dandy,Murphy(1995),”Genetic Algorithms Compared To other techniques for pipe optimization”, J.Water.Res.Plan.Magmt., vol.120(4),423-441
[12].David E. Goldberg ,Chie Hsiung Kuo,(1987),”Genetic algorithms in pipe optimization”,J.Comp.Civ . Eng.,vol.1(2),120-141
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 [email protected] ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








