高层建筑顶端冷却塔的拉索预张力优化计算

方明霞^１，韦林^１，康治国^２
(1.同济大学工程力学研究所，上海 200092；2.上海良机冷却塔设备有限公司，上海 201611)

　　摘　要： 通过求解非线性方程组，得到冷却塔拉索的最优预张力值，使冷却塔位于高层建筑顶端时其强度及刚度得到最优控制。
　　关键词：最优控制；冷却塔；拉索
　　中图分类号：TQ051.5
　　文献标识码：C
　　文章编号：1000-4602(1999)12-0031-03

　　 随着城市建设的日益发展，城市中的高层、超高层建筑越来越多，有相当数量的冷却塔被安置在高层建筑顶端。由于高处存在较强的风速 ,会使冷却塔结构产生较大的侧向位移,并提高结构的内应力值，这些位移和内应力值超过一定值后，将会使结构产生破坏。因此，在进行无风机科技冷却塔标准结构设计(当该冷却塔置于高层建筑顶端)时，在结构的某些部位预安置若干根拉索装置。由于风压高度系数增加，冷却塔某些部位的强度与刚度可能超过设计允许值，这时可张拉预安置的拉索装置来调节整塔的强度、刚度值，使塔体的所有部位满足强度及刚度要求。
　　如何在冷却塔产品设计时，既满足通常产品的要求，又可在原结构的基础上通过简单的改进措施，最优控制冷却塔位于高耸建筑顶端时其抗风载的能力，是非常值得研究的现实问题。

1　 数学模型建立

　　本文选取拉索的预张力为设计变量，考察冷却塔位于高层建筑顶端时其结构在风荷载作用下不满足强度、刚度要求的点作为控制点。假设第j根拉索的张拉力为X_j(j=1…n) ，则第i个控制点的强度σ应满足^［1］：

　　
　　式中　σ_i0——控制点的应力值
　　　　　σ_ij——第j根拉索张接力Xj的单位值引起该控制点的应力值

　　根据线性叠加原则，其叠加后的值应小于或等于允许应力值。同样当控制量为位移时，可写成位移控制方程：

　　
　　式中　△_i0——控制点的位移值
　　　　　△_j0——第j根拉索张拉力Xj单位值引起该控制点的位移值
　　如整个结构选取m个控制点，改造上述方程，并结合所有控制点的控制约束方程为：

　　

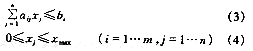
　　对上述结构控制约束方程进一步优化控制时，应考虑它的最优设计目标函数，而冷却塔结构优化设计的目标函数一般应从经济造价方面衡量，因拉索截面越小越经济，则在满足控制约束方程的条件下，索张拉力应尽可能小。因此写成拉索张拉力最优控制方程为：

　　

　　通过以上分析，得到利用预张力拉索来控制位于高层建筑顶端时冷却塔结构强度及刚度的最优控制方程为：

　　

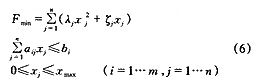
　　求解上述非线性规划方程组，即可选取最佳拉索张拉力，使冷却塔结构既可以满足不同高度风荷载的要求，又能最大限度地满足经济性要求。

2 无风机科技冷却塔的优化计算

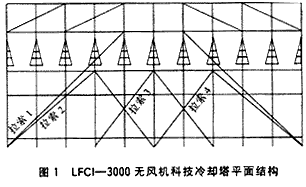
　　无风机科技冷却塔是冷却塔行业的最新产品，以前冷却塔结构主要以机械通风式冷却塔为主。随着社会和经济的发展，节约水资源和保护环境的呼声日益强烈，这些冷却塔逐渐暴露一系列诸如失水量大、噪声污染和水滴飞溅等问题。无风机科技冷却塔以高效率的流体动能转化装置取代风机作为空气动力装置，使传统式冷却塔难以克服的问题迎刃而解。本文以LFCI—3000无风机科技冷却塔为例，对其进行结构优化分析。由于该冷却塔结构的对称性，可以把它简化为X-Z平面内的平面结构(图1)，从图中可以看出各拉索的位置。

　　现考虑风荷载对该冷却塔结构的影响，根据文献［2］，垂直于建筑物表面的风荷载标准值按下式计算

　　Ｗ_k=β_zμ_sμ_zW₀式中　　β_z——Z高度处的风振系数
　　　　　　μ_s——风荷载体形系数
　　　　　　μ_z——风压高度变化系数
　　　　　　W₀——基本风压，kN/m²
　　　　　　W_k——风荷载标准值，kN/m²

　　经动力模态分析，塔体结构的自振周期为0.17s，小于0.25s，所以取β_Z=1。因无风机科技冷却塔为矩形结构，风荷载体形系数μ_S取为1.3。风压高度变化系数μ_Z随着高度Z的增加而增加。根据文献[3]，若冷却塔使用地区地面粗糙度为B类，则

　　μ_Z=(Z/10)^0.32式中 Z——冷却塔所处高度，m?

　　现将冷却塔置于100 m高层建筑的顶端，此时冷却塔底部的μ_Z=2.09，用有限元法计算得：σ_Amax=42.29 mm，σ_Bmax=248.4 MPa，此时冷却塔的强度、刚度均不足。分析发现，C、D、E三点的应力也较大，故取点A为位移控制点，点B、C、D、E为应力控制点。为比较风荷载对位于不同高度冷却塔结构的影响，表1列出10 m、100m高处控制点A的位移值及控制点B、C、D、E的应力值。

表1 同治同高度控制点的位移值及就力值 高度 控制点A的位移δA（mm） 控制点B的应力δB（MPa) 控制点C的应力δc（MPa） 控制点D的应力δD（MPa） 控制点E的应力δE（MPa） 10m标高处 12.88 120.84 102.39 103.26 113.84 100m标高处 42.53 248.44 218.76 218.46 235.54

　　从表中可以看出，当冷却塔位于100 m高处，在风荷载作用下其位移和应力值显著增加。
　　现考虑用张紧预张力拉索的办法来改变塔体的受力状况。取拉索的单位预张力为1kN, 用有限 元法分别求出单位预张力作用下冷却塔控制点A的位移值及控制点B、C、D、E的应力值,现把 计算结果列于表2。
　　把上述结果代入式(5)，并取加权因子为1，则优化LFCI-3000冷却塔拉索预张力的最优控制方程为：

　　
　　s.t.　-1.0x₁-0.52x₂-0.39x₃-0.39x₄≤-23.93
　　　　　-5.824x₁-6.181x₂-4.888x₃-4.887x₄≤-33.441
　　　　　-6.113x₁-6.639x₂-5.288x₃-5.287x₄≤--3.578
　　　　　-6.091x₁-6.631x₂-5.456x₃-5.307x₄≤-3.462
　　　　　-4.981x₁-5.610x₂-4.456x₃-4.454x₄≤-20.538
　　　　　0≤x1≤12.56 0≤x2≤12.56 0≤x3≤12.56 0≤x4≤12.56

　　将所有规划数据送入可求解非线性规划方程组的二次规划法［4］的程序中，最后求取的规划值为：

?　　　　x={11.362 11.362 8.575 8.575}?

　　即当冷却塔受到水平风荷载作用时，各拉索的最优预张力值分别为：
　　　　　x₁=11.362 kN,?x₂=11.362 kN,
?　　　　x₃=8.575 kN,? x₄=8.575 kN。
　　这时，即能最有效地使冷却塔位于100 m高度处满足其强度及刚度要求。

表2 单位预张力作用下冷却塔控制点的位移及应力值 拉索 控制点A的位移δA（mm） 控制点B的应力δB（MPa) 控制点C的应力δc（MPa） 控制点D的应力δD（MPa） 控制点E的应力δE（MPa） 拉索1 -1.0 -5.822 -6.113 -6.091 -4.981 拉索2 -0.52 -6.181 -6.639 -6.631 -5.610 拉索3 -0.39 -4.888 -5.288 -5.456 -4.456 拉索4 -0.39 -4.887 -5.287 -5.307 -4.454

3 结论

　　①对于类似于无风机科技冷却塔的矩形框架结构，在不改变原标准结构的基础上，用预留预张力拉索的办法，使冷却塔结构刚度重新分配，能最经济地满足冷却塔位于高层建筑顶端时其强度及刚度要求。
　　②利用本文推导的冷却塔结构强度及刚度的最优控制方程，可以求得冷却塔拉索预张力的最优控制值。
?　③用数学模型进行有效模拟，这种大型冷却塔拉索结构基于非线性分析的最优控制方法是可行的。

参考文献：?

　　［1］张炳华等.土建结构优化设计［M］.上海:同济大学出版社,1998.
　　［2］中国建筑工业出版社.结构工程师常用规范选［S］.北京:中国建筑工业出版 社,1994.
　　［3］张相庭.工程抗风设计计算手册［M］.北京:中国建筑工业出版社,1998.
　　［4］韦林，姜宏伟.群桩扩张位移的最优控制分析［J］.江西工 业大学学报，1991，13(2):611-615.

---

　　电　话：(021)65116755(H) 65983591(O)
　　传　真：(021)65116755?
　　E-mail:[email protected]
　　收稿日期：1999-05-14