采用遗传算法确定活性污泥模型的基本参数

采用遗传算法确定活性污泥模型的基本参数

段焕丰，俞国平，俞海宁
(同济大学污染控制与资源化研究国家重点实验室，上海 200092)

　　摘要： 采用遗传算法优化确定活性污泥数学模型中比较难以估值的动力学基本参数μ_M,A、b_H、μ_M、H和K_m,k等。结合模拟试验实例，将确定的上述参数与传统的方法结果进行了比较。结果表明，经遗传算法优化确定参数的单个误差在0.02%以内，总累计误差在0.1%左右，使得ASM模型参数具有较高的准确性和可靠性。
　　关键词：活性污泥；数学模型；动力学参数；遗传算法；污水处理

Determining basic parameters in activated sludge models by genetic algorithm

DUAN Huanfeng; YU Guoping; YU Haining

(National Key Lab of Pollution Control and Resource Reuse, Tongji University, Shanghai 200092, China)

Abstract： This paper introduced genetic algorithm to determine the basic parameters which were difficult to be valued in activated sludge models (ASM), such asμ_M、A,b_H,μ_M、H and K_m、k, and so on. And a simulated experiment showed the comparison between that method and traditional ways in values of parameters in the above. It also showed the activated sludge models (ASM) were more exact and reliable by optimizing their parameters which single error within 0.02% and total error also within 0.1%.
Keywords：activated sludge; mathematical model; kinetic parameters; genetic algorithm; sewage treatment;

　　活性污泥数学模型（ASM）的研究对于现行主要以活性污泥工艺的污水处理厂的投资设计与模拟运行具有重要的意义。经过近年的发展，ASM模型结构日趋完善。但是，到目前为止，其基本参数的确定仍然是研究者或者试验员们努力的重要方向，特别是对于动态变化过程中的动力学参数的确定尤为如此。本文通过对活性污泥工艺中组分的试验测定，结合遗传算法优化方法来确定基本参数值，进一步完善ASM模型。

1 ASM基本参数常用确定方法

　　ASM模型包括有ASM1、ASM2和ASM3三种基本模型。其中以ASM1模型最具影响。已有许多的研究者对这三种模型进行了修正与完善，使得它们更加符合实际应用^[1,2]。但是，不管它们经过怎样的修正与完善，其中有些参数是必不可少的，也是最基本的。这些参数包括有：自养菌最大比生长速率参数μ_M、A；异养菌衰减速率参数b_H；异养菌最大增长速率参数μ_M、H；水解速率参数K_m、k等。这些参数的常用确定方法有试验测定、模型拟合试验数据和系统辨识等^[3,4]。在对活性污泥系统实践应用过程中，这些方法确定的参数使得结果偏差较大。因此，提出新的方法对其参数优化有重要的意义。

2 利用遗传算法优化确定ASM参数

　　上述通过试验测定出来的参数值，一般都存在误差，包括试验误差和数据处理误差。为了减少试验误差，这些参数通常是经过多次试验，然后经过数据处理来估算其值。由于这些基本参数对模型的可靠性和准确性影响较大，而且它们本身具有很大的灵敏性，所以在进行数据处理时极小的误差就可能带来对整个模型的较大影响。实践表明，由于ASM模型结构复杂，通常使用的数据处理方法（如曲率法、最小二乘法或其他统计方法等等）很难保证结果的精度或者不能直接控制模型的精度。本文引入遗传算法对这些参数进行优化，无论ASM的结构如何复杂，该方法都能直接对模型的精度进行控制，使其达到预期的精度，具有较高的适应性。这是其他方法难以比拟的。
　　将遗传算法应用于ASM模型参数的优化中，建立优化模型如下：
2．1 优化模型的目标函数

（1）

　　式中：F——待优化的目标函数，为待求参数(x₁,x₂,…,x_n)的函数；
　　　　　(x₁,x₂,…,x_n)——待求参数，如本文中为μ_M、A、b_H、μ_M、H和K_m、k等；
　　　　　n——待优化参数个数；m(i)——ASM模型中与参数x_i有关的组分个数；
　　　　　T_i^p ——ASM模型模拟的组分浓度值；T_i^o ——试验实测的组分浓度值；
2．2 优化模型的约束条件
　　由于该算法直接对模型进行操作，所以某个待求的特定活性污泥数学模型ASM即为该优化模型的重要约束条件，也是主要约束条件。例如对ASM1模型，即为由13个组分和各个参数所组成的13阶非线性方程组^[2,4,5]。另外，对于每个参数有其初始取值范围，这也是约束条件之一。具体表达如下：

3 应用与检验

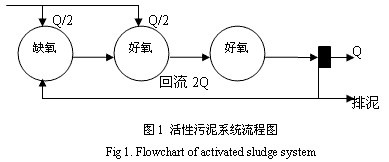
　　以ASM1为例，根据国际水质协会（IAWQ）报告^[6]，并设活性污泥系统如图1所示。该系统包括三个反应器，第一个为缺氧池，其余两个为好氧池；进水平均流入前两个反应器；污泥回流量为进水的2倍，假设无内回流；并假定二沉池为理想的泥水分离器，排泥量由SRT确定。以本文讨论的4个基本参数为变量优化，其余的参数值参照文献^[3]中的推荐值。设定优化模型的精度为0.1，试验PH值控制在中性环境附近，试验温度为17℃左右。

　　在优化过程中，遗传算法采用实数编码，以提高效率；群体规模n取200，选择算子采用比例选择方法，交叉杂交算子pc取1.0，变异算子pm取0.05。
　　各参数初始取值范围设定为：μ_M、A∈[0.20,0.90](d^-1),b_H∈[0.10,0.70](d^-1),μ_M、H∈[2.00,7.00](d^-1)和K_m、k∈[1.00,3.00](d^-1)。
　　经过GA－WEST软件优化计算，得到最优参数值为：

μ_M、A＝0.6021,b_H=0.5374,μ_M、H=4.4901,K_m、k=2.3116　　　

　　在计算结果中，模型（1）的累计相对误差为0.075（<0.1），最大单个相对误差<0.02。
　　稳态时，最优参数值对应的ASM1模拟结果与国际水质协会（IAWQ）报告^[6]中给出的结果对照比较如表1：

表1 ASM模型模拟值与IAWQ值

Table 1. Simulated values of ASM1 and IAWQ values

组分 缺氧反应器 好氧反应器1 好氧反应器2 模拟值 IAWQ 模拟值 IAWQ 模拟值 IAWQ

X_I
X_BH
X_BA
X_P
X_S
X_ND
S_S
S_NH
S_NO
S_ALK
S_I
S_ND
S_O
TSS 999.20 999.70 831.20 835.60 833.20 831.40 1601.20 1615.10 1366.50 1363.30 1362.50 1354.70 99.80 100.70 83.90 85.00 85.80 85.00 820.1 826.20 684.80 688.60 681.40 688.60 83.50 82.70 61.00 60.90 37.10 36.40 7.41 7.20 5.44 5.40 3.11 3.00 2.09 2.10 3.83 3.80 2.71 2.70 5.79 5.70 1.88 2.00 0.37 0.40 7.78 7.80 14.39 14.30 18.42 18.00 5.09 5.00 4.30 4.30 3.97 3.90 40.00 40.00 40.00 40.00 40.00 40.00 0.68 0.70 1.19 1.20 0.99 0.90 0.00 0.00 2.00 2.00 3.00 3.00 3615.07 3624.30 3029.96 3033.30 3006.70 2996.10

注：表中所有组分符号意义均参照国际水质协会（IAWQ）报告^[6]。

　　从上述计算优化结果来看，除了少数参数值有较大的误差外（误差在0.02%以内），优化参数值基本能符合实际值。这些误差较大的参数值可能受到温度、PH值等外界因素较大，从而产生相对较大偏差。这都说明该优化方法能够使参数达到较佳值。

4 讨论与结语

　　本文研究表明采用遗传算法对ASM模型进行优化计算，具有较强的实用性和和较高的可靠性。对于特定的ASM模型（ASM1，ASM2或ASM3等），在优化确定基本参数的同时，其他的参数假设为已知，即采取推荐的典型值，其实，除基本参数外的其他参数也可以通过该方法确定。只是鉴于其他参数的影响程度，一般采取推荐值即可。当然，该方法中的试验测定数据的准确性对结果影响较大。因此，对试验测定条件如PH值、温度等对参数确定的影响，需要进一步的研究，从而进行模型修正。

参考文献

[1] 徐伟锋，顾国维，张芳等．活性污泥3号模型（ASM3）的修正过程[J]．中国给水排水，2004，20（6）：29－31．

[2] 王闯．活性污泥数学模型研究．同济大学博士学位论文．2003．

[3] 刘芳，顾国维．ASM1模型中主要动力学参数的测定方法[J]．中国给水排水，2004，20（2）：37－40．

[4] 国际水协废水生物处理设计与运行数学模型课题组著．张亚雷，李咏梅译．活性污泥数学模型[M]．上海：同济大学出版社，2002．

[5] 宋兴志．活性污泥数学模型的研究．同济大学硕士学位论文．2001．

[6] Mogens Henze, Willi Gujer, Takashi Mino, Mark van Loosdrecht. Activated Sludge Models ASM1, ASM2, ASM2D and ASM3. IWA Scientific & Technical Report, No.9, 1999.

[7] 金菊良，丁晶．遗传算法及其在水科学中的应用[M]．成都：四川大学出版社，2000．

[8] 王育坚．Visual C++面向对象编程教程[M]．北京：清华大学出版社，2003．

---

作者简介：段焕丰（1982－），男，同济大学环境科学与工程学院

通讯地址：上海市四平路1239号同济大学环境科学与工程学院

邮编：200092

E-mail：[email protected]（段焕丰）