城市供水系统用水量的灰色预测

储诚山¹　　 祁淑艳²　 　　刘瑛³
1 天津大学　 2 天津天保市政公司　 3 安徽省岳西县自来水公司

　　摘要：利用灰色理论建模，对用水量分别进行短、中、长期预测，结果表明灰色预测能很好地应用于城市供水系统的用水量预测
　　关键词：灰色理论、灰色动态模型、用水量预测

The prediction of municipal water demand based on Grey Dynamic Model
1 Tianjin Uiversity 2 Tianjin Tianbao Municipal Co.ltd 3 Yuexi Waterworks Co.ltd, Anhui Province

Abstract: To set up a Grey Dynamic Model and to predict the municipal water demand of short 、middle and long term, the result shows that the GM can be used to the prediction of municipal water demand efficiently.
keywords: Grey theory、Grey Dynamic Model、water demand prediction

一 前言

　　对城市供水系统用水量的预测可分为短期预测、中期预测和长期预测。短期预测对制定供水计划、实现供水系统的优化调度具有重要意义；中长期的预测精确程度与否将直接影响到城市规划的规模、市政建设资金的投入与合理利用，以及水资源开发和规划等一系列问题。
　　灰色理论是80年代后提出的一种新理论，已广泛应用多部门的预测，证明具有较高的精度。大家知道，用水量多少与人们的生活习惯、气候变化、时间季节交替、节假日及工业发展水平等因素有关，但用水量和这些因素之间的准确函数关系却不得而知。如果把用水量当作一个系统，则它是一个灰色系统，对用水量预测问题可用灰色理论得到解决。本文的主要内容即是：利用灰色理论建模，对用水量分别进行短、中、长期预测，并编程计算、检验。结果表明灰色预测能很好地应用于城市供水系统的用水量预测。

二 城市供水系统用水量预测

2.1 预测模型的选择
　　灰色预测是基于灰色动态模型的(Grey Dynamic Model，简称GM)预测。灰色模型的通用公式为GM(n，h)，其中n表示微分方程的阶数，h表示变量个数。灰色理论主张用单因素一阶模型GM(1，1)作预测，把基于GM(1，1)模型的预测称为灰色预测。
2.2 GM(1，1)模型求解：

　　

　　M(1，1)模型的微分方程为：
　　若有原始数列(n>2时)：
　　x⁽⁰⁾=( x⁽⁰⁾(1), x⁽⁰⁾(2), x⁽⁰⁾(3), x⁽⁰⁾(4)···x⁽⁰⁾(n))
　　其1-AGO生成(一次累加生成)数列为

　　x⁽¹⁾=( x⁽¹⁾(1), x⁽¹⁾(2), x⁽¹⁾(3), x⁽¹⁾(4)···x⁽¹⁾(n))

　　构造以下矩阵：

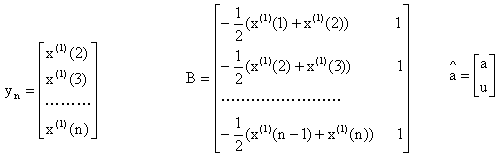
　　对GM(1，1)模型的微分方程求解，求得其时间响应函数为：

.3预测模型的精度检验
　　用灰色理论建立的初始模型不一定能反映序列的客观规律，还要对其进行诊断性检验，以考核模型的合理性。考核模型的方法称为精度检验，进行精度检验后，若不合格须对原模型进行修正或对残差建模。精度检验一般有三种方法，即：残差大小检验、关联度检验、后验差检验。这里，仅介绍后验差检验判断标准的具体指标：c——计算后验差比值，p——计算小误差概率，p、c的大小和预测精度等级关系见表1

表1

预测精度等级 p c 一级：好 >0.95　 <0.35 二级：合格 >0.8　 <0.5 三级：勉强　 >0.7 <0.65 四级：不合格 　 <0.7 >0.65

　　由矩阵B和向量y_k，根据式(1-1)可求得a、u的值，用Visual Basic语言编程实现该模型求解及检验过程，通过改变原始数据的个数和数据值，对未来某一个或若干个时间段内的用水量进行预测。

三 预测算例

　　以某一城市不同时间段内用水量为原始数据序列，用GM(1，1)对供水系统用水量进行短期和中长期预测。此过程中，用到等维灰数递补动态预测。所谓等维灰数递补动态预测，是指用GM(1，1)模型预测时，不是建立一个模型一直预测下去，而是用由已知数列建立的GM(1，1)模型预测一个值，而后将这个值补充在已知数列之后，同时去掉最老的一个数据，保持数列等维，再建立GM(1，1)模型，预测下一个值，将其结果再补充到数列之后，再去掉最老的一个数据，这样新陈代谢，逐个预测，依次递补，直到完成预测目标或达到一定精度为止。
3.1短期预测：
　　表2为连续七天，从中午1点到次日凌晨零点，12个小时内的用水量数据,以此为原始数据，预测第八天相同时段内的用水量(单位：吨/小时)。

表2 连续7天各小时用水量数据

时间h 第一天 第二天 第三天 第四天 第五天 第六天 第七天 1 44100 43675 40904 44449 44293 44005 41328 2 44064 43362 40882 45264 41327 42130 43584 3 42299 44126 41153 45055 44376 41768 42659 4 42690 43559 40567 44594 44788 41599 43112 5 43620 42447 40908 43548 44150 41795 42654 6 44918 43127 44513 45397 44086 47165 44898 7 51660 51708 52547 51589 50601 50893 48063 8 59075 60420 61736 58569 59490 57988 57699 9 60435 55148 56976 58589 58938 59772 59333 10 57223 61937 59938 57650 59145 59443 60685 11 62219 57806 58842 59337 58017 62592 56761 12 58663 61493 60343 61297 58939 60176 59536

　　采用相对误差θ来检验其预测精度，表3为第八天用水量实际值和预测值的关系比较。其中: %θ=100*(际值-预测值)/实际值

表3 第八天实际用水量和预测用水量关系比较

时间h

实际值

预测值

θ(%)

时间h

实际值

预测值

θ(%) 1 44253.00 42854.19 3.16 7 50580.60 48549.00 4.02 2 42772.00 42850.41 -0.18 8 56751.00 56962.00 -0.37 3 43029.00 42500.06 1.23 9 62814.00 61120.16 2.70 4 44178.00 43141.50 2.35 10 61196.00 59166.50 3.32 5 43149.00 43011.97 0.32 11 60199.00 59358.16 1.40 6 46687.00 46421.75 0.57 12 60831.00 59039.97 2.94

3.3中期预测
　　表4为1994——2001年的月用水量和年用水量数据(单位为千吨)

表4 1994——2001年的月用水量和年用水量数据

月份 1994年 1995年 1996年 1997年 1998年 1999年 2000年 2001年 1 37837.08 37868.14 36959.48 38801.93 38977.33 39403.33 39644.40 39208.02 2 37023.23 37101.26 35789.69 36878.95 37795.21 38168.96 37643.34 38265.36 3 37928.50 38522.65 37732.71 38401.70 39449.30 39305.93 39071.95 39903.05 4 39440.73 39594.30 38964.04 39355.42 40892.34 39937.93 40268.08 41248.67 5 44019.94 44346.98 41206.46 42247.10 44850.95 42774.21 43042.08 45424.63 6 41568.57 41876.70 41639.80 42793.54 44822.19 42923.03 44623.25 45073.68 7 37866.35 38734.39 39242.99 40752.26 41420.12 39148.13 43852.09 45076.94 8 37539.80 37913.84 39910.06 39926.39 39033.86 40018.03 41107.00 39008.69 9 35376.35 37097.93 37636.37 36865.09 37085.67 38793.35 39978.42 37625.43 10 36571.95 37694.35 38470.14 38095.64 37322.50 39405.95 39864.56 39583.13 11 34064.79 33595.65 35602.02 34484.67 33185.39 34704.76 34638.20 35291.90 12 37236.53 37532.44 39512.86 37618.81 38420.10 39871.44 40452.15 41208.73 合计 456473.8 461878.6 462666.6 466221.5 473255.0 474455.1 484185.5 486918.2

　　由1994——1999年的月用水量数据，用等维灰数递补动态预测法预测2001、2000两年的月用水量，实际值与预测值关系见表5

表5 2001、2000两年中月用水量实际值与预测值比较

月

份

2001年

2000年 实际值 预测值 θ(%) 实际值 预测值 θ(%) 1 39208.02 40489.64 -3.27 39644.40 39955.56 -0.78 2 38265.36 38907.39 -1.68 37643.34 38453.39 -2.15 3 39903.05 40020.88 -0.30 39071.95 39681.20 -1.56 4 41248.67 40808.88 1.07 40268.08 40540.27 -0.68 5 45424.63 43347.78 4.57 43042.08 43276.94 -0.55 6 45073.68 44953.75 0.27 44623.25 44406.25 0.49 7 45076.94 43660.80 3.14 43852.09 42806.55 2.38 8 39008.69 40702.01 -4.34 41107.00 40362.19 1.81 9 37625.43 38657.09 -2.74 39978.42 38362.80 4.04 10 39583.13 39122.75 1.16 39864.56 38889.03 2.45 11 35291.90 34235.47 2.99 34638.20 34255.20 1.11 12 41208.73 40054.69 2.80 40452.15 39682.73 1.90

3.3长期预测
　　由表4知1994——2001年各年用水量数据，用1994——2000年7年的年用水量，预测2001年年用水量为485449.3千吨，而实际值为486918.2千吨，相对误差为θ=0.30%。因为数据较少，不能说明长期预测有较高精度，于是，我们再用其他方法对预测模型的精度进行检验，经上机计算后，结果如下：
　　后验差检验： p=1(好)　 c=0.2060(好)

　　

　　求得的预测模型为：

　　 (t=1,2,．．．6)

　　残差检验结果见表6：

表6

年份 原始值 模型值 残差比(%) 1995 461878.6 459576.0 0.50 1996 462666.6 463790.4 -0.24 1997 466221.5 468043.5 -0.39 1998 473255.0 472335.5 0.19 1999 474455.1 476667.0 -0.47 2000 484185.5 481038.0 0.65

四 灰色预测分析

　　就以上预测结果可以看出：
　　GM(1，1)灰色预测模型能应用于城市供水系统的用水量预测，并且精度较高。笔者曾用灰色理论和神经元网络理论，对相同的用水量数据进行同一条件下的预测，预测结果表明，前者的相对误差值比后者的相对误差值在总体上更能让人接受。
　　对于灰色预测，预测的范围越大，则互补的因素越多，主观因素就越少。所以就用水量预测来说，月用水量预测明显比小时用水量精度高(由表3、表5中的θ值即知)。虽没有比较数据，但对大中城市的用水量预测一定比对小城市用水量预测的精度高，这在理论逻辑上也能为人理解和接受。
　　利用等维灰数递补动态预测法，就可由较少的原始数据建立预测模型进行预测，而且有较高的预测精度，这就使得灰色预测比时间序列法和概率统计等方法对用水量预测有更好的优越性。
　　此外，灰色预测有多种改进途径，以减弱极端值的影响，强化原始数列的大致趋势，尽可能将原始数列改造成指数递增变化的序列，这种改进方法对于特殊时间(如节假日和某一非常气候)的预测极其有效。
　　诚然，单因素的灰色预测模型对于多因素的长期预测有其局限之处，但是，灰色预测对制定供水计划和实行优化调度仍具有重要意义。

---

作者简介：储诚山，男，安徽人，博士研究生，工程师，从事给水系统优化与数学模型研究
通讯地址：天津保税区东方大道193号公用公司
电话：022-81818517或65750169 传真：022-65750184
email:[email protected]