泵站拍门的动态系统分析与优化设计探讨
| 论文类型 | 其他 | 发表日期 | 2003-04-01 |
| 来源 | 中国水网 | ||
| 作者 | 张大群 | ||
| 摘要 | 张大群 (天津市市政工程勘测设计院) 在大型泵站中,由于正常停泵或一旦动力中断造成的事故停泵,会使水体逆流,水泵倒转,严重的会使水泵遭到破坏,造成事故,影响系统的正常运行。因此,大型泵站水泵止逆方式是一项重要的研究课题。 目前,国内在大型泵站中采用的止逆方 ... | ||
(天津市市政工程勘测设计院)
在大型泵站中,由于正常停泵或一旦动力中断造成的事故停泵,会使水体逆流,水泵倒转,严重的会使水泵遭到破坏,造成事故,影响系统的正常运行。因此,大型泵站水泵止逆方式是一项重要的研究课题。
目前,国内在大型泵站中采用的止逆方式通常有虹吸断流、快速闸门断流及拍门断流等三种.拍门断流是在流道出口处安装一个带有钱链的止逆阀门.当正常运行时,靠水流冲力将门体顶开而出流,停机后水流对拍门的冲力迅速减小,门体靠自重而下落.当水泵正流阶段结束后,水流冲力消失,随之水体逆流,拍门转为受反向水压力作用.在门重和反向水压力作用下,拍门关闭并压紧出水流道管口。其工作示意图见图1。
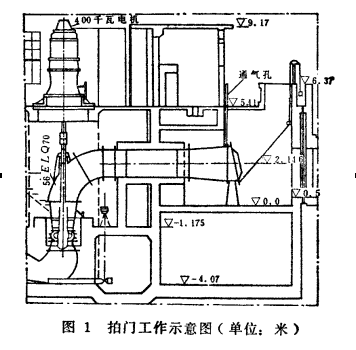
在一定条件下,由于拍门断流这一止逆方式有较好的技术、经济效果,故近年来已在大型泵站中使用.但它仍存在着过流水头损失较大和停泵时拍门对门座撞击力过大的问题。因此,如何在尽可能减小过流水头损失的情况下将撞击力减至最小,乃是研究拍门断流的重要问题,尤其对大型泵站更为重要.为解决大型泵站中的拍门过流水头损失较大及停机时拍门对门座撞击力过大的问题,本文从拍门的动态系统分析出发,定性及定量地分析了拍门下落中多变量之间的相互影响;将拍门的下落运动划分为若干阶段,建立各阶段约束条件与目标函数之间的数学模型;计算并选择出每一阶段的"子最优化"值,再逐步包含在全程最优化策略中,以达到设计的全程优化;从而提出了拍门优化下落过程的程序数值计算方法,并编制了相应的电算程序。经水工模型试验验证,可使拍门在不增大过流水头损失的前提下,撞击力减少50~75%,为解决大型泵站拍门撞击力的问题,提供了一条途径.此外,本文还就天津南国堤河泵站工程的56ZLQ-70型泵拍门优化下落过程的程序数值计算作一简介,计算结果,在过流水头损失不增大的情况下,可使拍门撞击力由29吨减至8吨左右。
一、设计变量与优化设计的计算过程
在拍门优化下落过程的程序数值计算中,存在着多种设计变量(亦即优化设计的择优参数),其中有拍门门重、开启角(即下落初始角)、外拉力施加值、外拉力作用点与门铰的水平和垂直距离、进出水流道长度、出水管
直径、出水口形状(圆形、方形)、拍门形心、吊点至上铰距离,以及缓冲橡皮特征(接触面积、厚度、弹性模最)等。
拍门从开启至下落的运动过程比较复杂,在不同状态下的受力分析见图2所示。
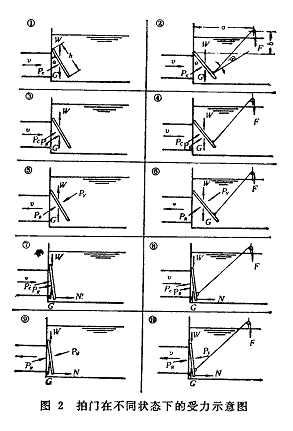
在对拍门进行动态系统分析和下落过程的程序数值计算中,按其时间与逻辑的顺序可划分为6个阶段.各阶段所建立的数学模型,详见参考文献[1]、[3]。现将6个阶段优化设计的计算步骤简介如下(图3)
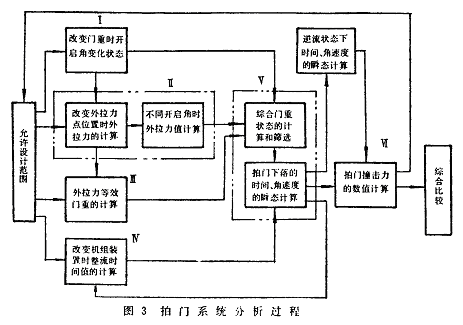
1.拍门的过流水头损失与开启角有关。据有关资料介绍:开启角为45。时,水头损失系数ε<0.6;50°时,ε<0.3;60°时, ε<0.1。门重是影响开启角的重要因素,为此,在第I阶段优化设计的计算中,将31种不同的门重分别输入第I阶段数学模型中进行运算,得出相应的开启角数值,并将开启角在50。左右的门重值输入有关阶段进行计算分析,见图3中之I。
2.在一些情况下,需要施加外拉力来增大开启角和减小撞击力.而外拉力的作用点与拍门上铰的水平和垂直距离(即α、b值,见图2-②)的不同组合对拉力矩数值影响甚大。为此,第Ⅱ阶段优化计算是在一种固定门重下,取7种不同的开启角,并将20组不同的α、b组合值分别输入第II阶段数学模型中运算,得出7种开启角的最小拉力值以及与其相应的拉力作用点的α、b组合值,然后进入下一阶段的计算及分析,见图3中之II。
3.因带有外拉力的拍门系统,其下落运动的计算较为复杂,但如利用在每一瞬态α、β角(见图2一②)之间的几何关系,将外拉力数值用等效门重的形式来表达,这虽使门重的变化幅度加大,但是由于减小了外拉力这一变量参数,所以计算将大为简化。为此,优化设计计算的第III阶段是将20种不同的外拉力数值在7种不间开启角状态下,分别输入此阶段的数学模型中运算,得出各种开启角状态下的等效门重值,然后输入下一阶段,见图3中之III。
4.正常运行的水泵,若动力突然中断,则由于惯性作用,水泵和管道中的水流将继续以原有的方向流动,但速度逐渐减小,压力逐渐降低,直至速度为零,称这种惯性水泵工况所经历的时间为水泵停机后的正流阶段时间。正流时间的长短对撞击力影响甚大,而机组的转动惯量、扬程、流量,以及进、出水流道长度,流道口面积等都对正流时间有直接的影响.为此,在第IV阶段优化计算中,系将3组不同工况、4组不同管道长度、4组不同管道直径,分别输入惯性水泵工况的数学模型中运算,计算出各种状态下的正流阶段时间,然后输入下一阶段,见图3中之IV。
5.将上述第1、II、III阶段所得的门重、外拉力、等效门重合并成综合门重(门重+等效门重),并进行拍门下落到关闭位置的瞬态角速度及时间的计算。第V阶段优化计算就是将3种综合门重,在3种初始角状态下,分别输入此阶段的数学模型中,将计算出的拍门下落时间与第IV阶段所得正流时间依此比较,然后将小于正流时间的下落时间输入下一阶段,见图3中之V。
6.将上述选出的状态进行拍门下落撞击力的计算。第VI阶段优化计算,即将不同工况、不同条件下拍门下落的时间小于正流时间的18组状态输入本阶段数学模型中,以计算撞击力值。并将所得出的最小撞击力及由此而依次前推听得出的各阶段数值为拍门的优化设计结果。见图3中之VI。
二、优化设计的计算结果分析
按上述拍门优化设计的计算步骤,对天津南国堤河泵站工程的拍门进行了数值计算,现将择优选取有关诸参数在各计算阶段中所得到的计算结果点绘于图4中。
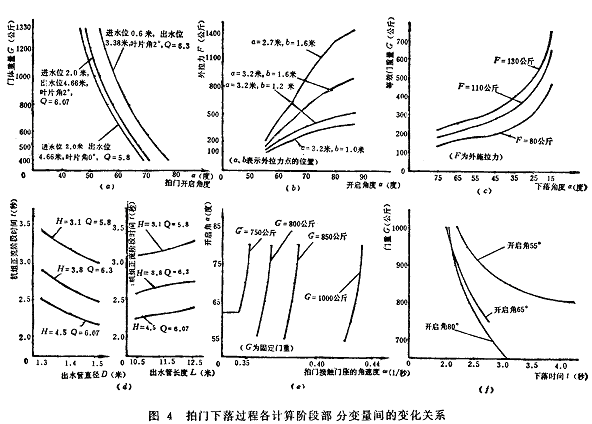
为表明拍门优化下落过程的程序数值计算对其产生撞击力数值的影响,特将在一种工况门重分别为1,000公斤、850公斤、800公斤、750公斤,下落初始角为55°和65°,在不带平衡重和带平衡重,带平衡重中又分为下落时仍带平衡重及下落瞬间脱开平衡重两种,即综合为3种状态下落时的撞击力数值比较,列于表1。
从表1中的计算值及相应水工模型试验与计算结果可看出以下几个问题:
1.经上述第II阶段对外拉力作用点与拍门上铰的水平和垂直距离的优化计算,得出了使拍门开启到各种确定角度的外拉力最小值。在这个前提下,对不同的门重、不同的开启角所计算出的撞击力数值,仍在6~18吨的范围内变动,相差3倍左右。若不经过第II阶段的优化,则相差更为悬殊。例如,取施加在拍门上的外拉力作用点与门钱中心的水平距离α=3.2米,垂直距离b=1.6米,则当门重为1,000公斤、开启角为65°、外拉力为443公斤时, 可计算出下落至关闭位置时的角速度为1.89/秒,撞击力为29.47吨,这比进行优化的数值约增大4倍左右。
2.在同样条件下,下落时带平衡重比下落时瞬间脱开平衡童的撞击力要大。如表中状态I与II,V与VL VII与VIII,IX与X等,这是因为外拉力的存在,增大了下落的阻尼力矩,延缓了下落时间,以致在全关时,已进入了逆流阶段所致。反之,如拍门下落到关闭位置仍处在正流阶段,则带有平衡重时的撞击力比下落时瞬间脱开平衡童时的反而要小。例如,在数值计算中可知,当门重为1,000公斤、外拉力为95公斤、开启角为52°时,下落到关闭位置的时间处于正流阶段,故撞击力仅为6.41吨,小于表l中状态I的7.574吨。
3.在所取工况下,三种不同状态的优化设计计算分别为:
(1) 不带外拉力的是状态Ⅲ。
(2) 带外拉力开启又带外拉力下落的是状态II。
(3)带外拉力开启而又不带外拉力(瞬间脱开)下落的是状态IX。
上述三种不同状态优化设计的全程设计结果,也称为这个状态的最优化策略。组成最优化策略的每个阶段所得的数值称为"子最优化"值。它使得在水头损失尽可能减小的情况下,撞击力减至最小.虽然在拍门下落过程的每一阶段中,它并不一定是该阶段数学模型运算出的最大或最小值,但却是符合全程目标的最优值。
表1不同门重、不同开启角时拍门撞击力数值比较
开启角α 门重(公斤) 状态序号 平衡重
(公斤) 正流结束时下落角 拍门关闭时
水流所处阶段 折门下落到关闭
位置的时间(秒) 接触门座时的
角速度(1/秒) 撞击力
(吨) 55° 1,000 Ⅰ 下落脱开 6° 正流 1.6866 0.4199 7.574 Ⅱ 110 14° 逆流 2.4123 0.3901 9.056 850 Ⅲ 无 10° 正流 2.1212 0.3757 6.837 800 Ⅳ 无 12° 逆流 2.3993 0.3604 8.489 65° 1,000 Ⅴ 下落脱开 5° 正流 1.6248 0.4275 7.711 Ⅵ 234 22° 逆流 5.5302 1.4508 18.680 800 Ⅶ 下落脱开 8° 正流 1.8902 0.3663 5.910 Ⅷ 130 21° 逆流 5.3808 1.3918 18.210 750 Ⅸ 下落脱开 10° 正流 2.1299 0.3502 5.471 Ⅹ 96 23° 逆流 5.7611 1.3950 17.780
三、拍门动态系统分析的描述
在拍门优化设计中,其目标是开启角越大越好,撞击力越小越好。为此,第一个方法是减轻门重,这样,门体轻了,下落时间就加长。若时间加长后仍在机组正流阶段结束之前全关,则在强度、刚度诸条件保证的前提下减轻门重愈多愈有利。但加长后的时间超过了正流阶段时间,由于正向水流已消失,拍门处于反向动水压力的作用下,所以撞击力反而增大了。此时,如再继续减轻门重,撞击力则会成倍增加,并且还会出现反复撞击多次的现象。
第二个方法是增加外拉力,外拉力的存在无疑对增大开启角是有益的。但停机下落过程中必然会增加一个由外拉力而产生的阻尼力矩,因而减缓了拍门下落的速度.倘此时下落仍在正流阶段结束之前,则由外拉力产生的阻尼力矩可削减拍门的撞击力,且外拉力数值的正向增加愈多愈有利。但一旦下落时间超过了正流阶段时间,则在逆流的作用下,增加了拍门下落的最终角速度,因而增大了拍门的撞击力。此时以施加外拉力来试图削减撞击力的方法则是不可取的.如继续增加外拉力,撞击力不仅增加,还会造成停机后拍门不能关严、水体逆流等状况.关于外拉力对撞击力数值的影响分析见表2。
表2 外力拉力对拍门撞击力数值的影响
序号 进水位(米) 出水位
(米) 拍门扬程
(米) 门重
(公斤) 开启角 外拉力
(公斤) 拍门下落状态 拍门接触门座
时所处阶段 撞击力
(吨) 备注 Ⅰ 0.62 3.39 2.77 1,350 66.7° 112.4 带拉力下落 正流 8.377 正流阶段外力大,撞击力小 Ⅱ 0.62 3.39 2.77 1,350 66.7° 112.4 脱开下落 正流 9.371 Ⅲ 1.99 4.68 2.69 1,350 55° 217.5 带拉力下落 逆流 10.933 逆流阶段外力大,撞击力大 Ⅳ 1.99 4.68 2.69 1,350 65° 420.5 脱开下落 逆流 24.563
综上所述,为使拍门在机组正流时间内关闭,应结合泵站总体设计对进、出水流道长度,出水管直径,机组转动惯量,以及进、出口水位等作适当调整。根据计算和试验可知,加长出水流道长度、减小出水管直径、加大转动惯量、降低扬程等措施对增加正流时间有益。
由以上分析可知,上述目标的确定与多种参数有关。门重作为一个重要的择优参数,当它随一个目标向好的方向变化,有时却导致另一个目标向坏的方向变化。除门重外,初始开启角、外拉力数值、外拉力作用点位置等的变化都会使目标发生相似的影响。因此,由这些变量参数所导致或组成的撞击力与开启角的双重目标,有时相互协调,有时相互矛盾,这种复杂的变化关系,只有借助于电算,才易于求解。其示例见图5。
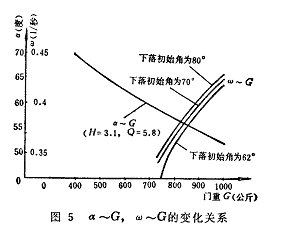
本文运用动态系统分析,在上述定性、定量地分析各变量参数之间相互关系的基础上,通过电子计算机对各种择优参数按拍门优化下落的设计程序进行迭代计算,并比较计算所得出的上百个可行方案,从中择优选择过流水头损失尽可能小而又使撞击力减至最小的方案作为拍门的优化设计方案。
这种动态系统分析方法是z首先将系统的运动划分为若干阶段,将每个阶段均列出求解阶段目标函数的数学模型.虽然通过常规的优化方法,可得出每一阶段的最大或最小值,但每一阶段分别进行优化,并不能造成系统最优化策略的实现.有的变量参数在一个方向的递增会对这个阶段的优化选择有利,而对下一阶段则可能有害.甚至在某一阶段为进行阶段优化而作的特殊改进,还会使系统总体性能恶化。为此,就需对系统每一阶段的一些元素或条件,进行一定的选择和调整,将一些元素或条件之间的矛盾与互异的状态,综合成有条理而协调的结构。
四、采用的最优化方法及电算程序
拍门系统的运动是由多个阶段所组成一,因此,本课题采用了动态规划的方法进行优化设计,其最优化的原则如图6所示。
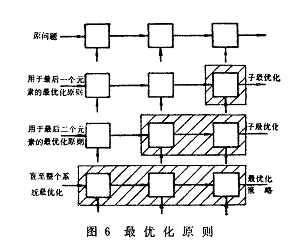

如果以di表示决策变量(即设计者可对它控制并可处置的变量),Si、 ~Si为输入、输出状态变量(系依附于决策变量,因而不能为设计者直接控制的变量),系统的阶段用1~n表示,ri为阶段效益,R为最优化策略,则在这种多阶段优化设计中,信息过流顺序如图7所示(数学表达式从略)。
拍门优化下落计算程序采用FORTRAN语言.输入常、变量参数29个。全机运算40分钟(包括宽行输出)。程序的框图见图8,有关程序结构、功能、特点见参考文献[4]。
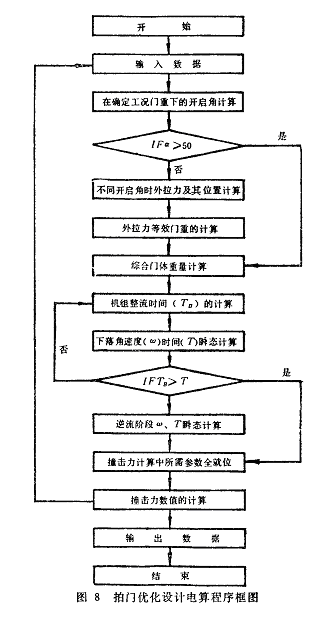
五、结束语
1.在泵站装有拍门情况下的某些流体运动机理,迄今不很清楚,尽管计算工具和方法有了相应的提高和发展,但由于计算中的假设及边界条件存在的局限性,完全真实地反映拍门运动的规律是困难的。但在同样精度的前提下,通过优化设计,可使撞击力减小,这就为解决大型泵站拍门撞击力问题,提供了一条可行的途径。
2.本文分析主要集中于任一种工况,对于不同的工况,其拍门的撞击力及下落过程参数是不同的(见图4)即使同样流量、扬程, 而进、出水位不同,其撞击力及开启角仍存在一定的或较大的差异,见表3。
表3 进、出口水位对拍门撞击力数值的影响
序号 叶片角 进水位(米) 出水位(米) 拍门扬程
(米) 开启角 外拉力
(公斤) 撞击力(吨) 备注 Ⅰ 1 2° 0.62 3.38 2.77 61.7° 0 7.099 净扬程相同,出水位越高,撞击力越大 2 1.97 4.66 2.69 52.5° 0 7.951 Ⅱ 3 0° 0.67 3.46 2.79 65° 195 8.188 4 1.99 4.68 2.69 65° 420 24.563
为此,在优化设计中应该按照不同工况, 不同进、出水位分别予以分析。
3.一般在直管式出水流道中都应安装通气孔,这对减小拍门的撞击力及管内的负压是有益的。通气孔一般布置在流道突起的最高位置,对于上升管应布置在拍门出口附近。由于拍门外往往是明流,故在本文的优化设计中, 未考虑水锤波的影响。
4.采用动态规划的系统分析并进行优化设计,就要对每种状态变量反复进行迭代运算。对于大量信息的处理问题,各变量参数对于后面阶段的变化影响以及对关键变量步长的选取及分析综合的技巧问题等,在此不作介绍。
参考文献
[1] 江苏农学院机电排溉研究室,泵站拍门的运动和撞击探讨.江苏农学院学报,1981年第2期。
[2] 华东水利学院、天津市IE政工程勘测设计院,天津南围堤河泵站试验报告。1981年12月。
[3] 张大群,泵站拍门的最优化设计与分析。天津市市政工程勘测设计院,1982年3月。
[4] 张大群,泵站拍门优化设计的电算程序简介。天津市市政工程勘测设汁院,1982年10月。
[5] Bellman, R.E., Dynamic Programming. Princeton University,1957.
[6] Bellman, R.E., Dreyfus, S., Applied Dynamie programming. Princeton University.1962.
[7] Wilde, D.J., Beightler, C.S., Foundations of Optimization. 1967.
[8] (美)罗道福。J.阿奎拉,规划设计施工中的系统分析与设计。1981年。
*本文承蒙孙连溪、朱肇源、高复栋同志的审阅及指导,并到得严登丰、田家山、张洪楚、仲付维、刘大恺、周鹏、姜伟等同志的指点与帮助,特此致谢。
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 [email protected] ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








