采用遗传算法优化设计排水管道系统

李树平
(上海市苏州河综合整治建设有限公司，上海200002)

　　摘　要：采用遗传算法 对已定管线的排水管道系统进行了优化设计，首先引入可行管径集的概念，直接利用标准管径并将各管段的管径映射为适合于遗传算法操作的编码形式。其中污水管道可行管径集系根据设计流量和最大设计充满度来确定，雨水管渠和合流制管渠可行管径集系根据直接优化法计算结果来确定。实际算例表明，该方法的计算结果既能满足设计规范的要求，又可节约工程投资。
　　关键词：可行管径集；遗传算法；排水管道系统；优化设计；编码
　　中图分类号：TU992
　　文献标识码：C
　　文章编号：1000-4602(2002)12-0059-04

　　应用最优化方法进行已定管线的排水管道系统优化设计计算时主要面临以下几个问题：① 管道直径不是连续的，而是离散的；②设计计算模型的目标函数和约束条件大多是非线性的；③优化过程运行时间的长短、占用内存量的大小；④管段与管段设计之间不满足“无后效性”；⑤怎样减少人为干预，使尽可能多的工作由计算机完成^［1］。为了尽可能地解决这些问题，在排水管道优化设计中引入了遗传算法。

1　可行管径集和编码映射技巧

　　可行管径集的定义为：在某一确定流量下，能够满足规范规定的流速、坡度和充满度等水力条件约束的一系列规格管径的总体^［2］。例如在一个排水管道系统中，若每个管段具有4个可供选择的规格管径，那么有100根管段的系统将有4100种具有不同工程造价的方案可供选择。
1.1 污水管道系统
　　根据流速和坡度约束，某一固定管径的设计流量范围应为：
?　　　Q∈［f(v_min),f(v_max)］I［f(I_min),f(I_max)］
　　因为I_min是在流速为v_min、充满度为(h/D)min时求得的值，所以当(h/D)＞(h/D)min且逐渐增大时则θ值越来越大。根据三角函数性质，当θ由0→2π时，sinθ/θ越来越小、R值则越来越大、v值越来越大，此时即使I=I_min，v值也将大于v_min。因此，总是有f(v_min)≤f(I_min)。又由于在最大设计充满度时，I_max是在流速为v_max、充满度为(h/D)max时求得，所以f(v_max)=f(I_max)，此时设计流量范围为［f(I_min)，f(I_max)］。不同管径在最大设计充满度时的设计流量范围见表1。

表1　不同管径在最大设计充满度时的设计流量范围 (部分) 管段管径D(mm) 最小设计流量Q_min(L/s) 最大设计流量Q_max(L/s) 管段管径D(mm) 最小设计流量Q_min(L/s) 最大设计流量Q_max(L/s) 200 11.28 42.49 500 115.20 352.34 250 19.13 66.39 600 189.14 507.37 300 28.81 95.60 700 257.61 69.058 350 45.81 158.88 800 336.28 901.98 400 57.03 207.52 900 426.89 1141.57 450 72.20 262.64 1000 480.42 1516.44

　　为了充分利用管道的通水能力，在设计中一般选择尽可能大的设计充满度。例如，某一管段设计流量为Q=300L/s，由表1可知在最大设计充满度的情况下，可选管径有500、600、700mm等三种，它们构成了可行管径系列集。如果选择四种可行管径作为优化对象，则选择500、600、700、800mm(在遗传算法中以二进制编码表示，分别为00、01、10、11)。?
1.2　雨水管渠系统和合流制管渠系统
　　由于设计管段内的雨水流量与其流经上游管线的时间有关，因此不像污水管道那样直接采用设计流量来选择可行管径，而是要建立在直接优化法的基础上。直接优化法在程序设计中采用的方法是：只有当计算管径比较接近比其大一级的规格管径时才选择大一级的规格管径，反之则选择小一级的规格管径^［3］。于是可行管径集的计算方法为：对于某一设计管段，如果用直接优化法求出的管径为D，则该管段的可行管径集采用{prev(D)，D，succ(D)}，其中Prev(D)和Succ(D)分别是规格管径中D的上一级和下一级管径。例如某一设计管段由直接优化法所求出的管径为500mm，则选择450、500、600mm三种规格管径组成可行管径集，如果在遗传算法中采用十进制编码，将分别以0、1、2表示。
　　合流制管渠系统一般按满流设计，其水力计算的设计数据包括设计流速、最小坡度和最小管径等，基本上与雨水管渠的设计相同^［3］。合流制管渠的雨水设计重现期可适当高于同一情况下的雨水管渠。其可行管径集的确定及编码映射技巧与雨水管渠系统类似。

2　遗传算法优化设计

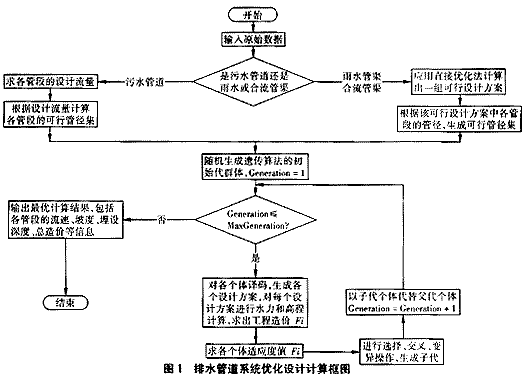
　　在确定排水管道中各管段的可行管径集的基础上，把设计管段的可行管径映射成遗传算法中的编码，再对这些编码进行选择、交叉和变异等遗传操作，就可以应用遗传算法解决已定管线下排水管道优化设计计算问题。优化设计计算框图见图1。

3　算例分析

3.1 算例1
　　算例1为某市一个区域污水干管设计，表2是采用遗传算法与直接优化法的计算结果比较。

表2　应用不同方法计算结果比较(算例1) 管段编号 管道长度L(m) 设计流量Q(L/s) 直接优化法^［2］ 遗传算法 管径D(mm) 坡度I(%) 流速v(m/s) 埋设深度(m) 管径D(mm) 坡度I(%) 流速v(m/s) 埋设深度(m) 上端 下端 上端 下端 1～2 110.0 25.00 350 0.306 0.700 2.00 2.24 350 0.305 0.700 2.00 2.24 2～3 250.0 38.20 350 0.237 0.710 2.29 2.83 350 0.237 0.710 2.29 2.83 3～4 170.0 39.52 350 0.240 0.720 2.83 3.19 350 0.240 0.720 2.83 3.19 4～5 220.0 61.10 400 0.189 0.730 3.25 3.57 400 0.189 0.730 3.25 3.57 5～6 240.0 67.10 450 0.182 0.740 3.62 3.95 450 0.182 0.740 3.57 3.90 6～7 240.0 84.69 500 0.161 0.750 3.98 4.27 450 0.177 0.771 3.94 4.27

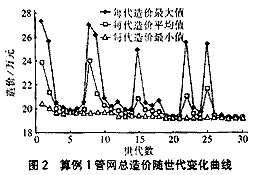
　　从表2可以看出，两种计算结果都满足排水管道设计规范的要求。但应用同样的造价函数，直接优化法计算的工程费用为196 474.1元，而遗传算法计算的工程费用为191923.80元，比直接优化法低4550.3元(节省2.3%)。两算法对管段1～2、2～3、3～4、4～5的设计参数基本相同。在管段5～6，直接优化法在节点5变管径处采用了管顶平接，而遗传算法程序采用了水面平接与管顶平接相结合的办法来处理。在管段6～7，经遗传算法计算得到的管径比直接优化法小一级，流速和充满度、坡度均大于直接优化法的结果。管网总造价随遗传世代变化曲线见图2。

3.2　算例2?
　　算例2是对某市一个区域的截流式合流干管的设计，该截流干管具有13个管段。表3是采用遗传算法与普通查图表方法的计算结果比较。

表3 应用不同方法计算结果比较(算例2) 管段编号 管道长度L(m) 普通查图表方法^［3］ 遗传算法 设计流量Q(L/s) 管径D(mm) 坡度I(%) 流速v(m/s) 埋设深度(m) 设计流量Q(L/s) 管径D(mm) 坡度I(%) 流速v(m/s ) 埋设深度(m) 上端 下端 上端 下端 1～2 75 52.4 300 0.28 0.75 1.70 1.71 53.51 350 0.245 0.75 1.70 1.68 2～3 75 162 500 0.17 0.81 1.91 1.84 163.47 500 0.187 0.83 1.83 1.77 3～4 100 288 600 0.21 1.01 1.94 1.90 291.83 700 0.123 0.84 1.97 1.85 4～5 80 327.54 600 0.27 1.15 1.90 2.12 320.52 700 0.125 0.85 1.85 1.95 5～6 120 626.58 800 0.22 1.23 2.32 2.53 602.79 900 0.111 0.95 2.15 2.23 6～7 150 838.47 900 0.21 1.32 2.63 2.89 795.16 1000 0.110 1.01 2.33 2.45 7～8 300 260.88 600 0.18 0.95 2.89 3.48 259.40 600 0.222 1.02 2.45 3.16 8～9 270 455.46 700 0.22 1.15 3.58 4.12 422.44 800 0.154 1.03 3.36 3.73 9～10 300 515.59 700 0.27 1.27 4.12 4.93 512.21 800 0.157 1.04 3.73 4.20 10～11 230 382.16 700 0.25 1.25 4.93 5.50 379.02 700 0.191 1.05 4.20 4.64 11～12 280 584.82 800 0.18 1.17 5.60 6.16 568.97 800 0.185 1.13 4.74 5.31 12～13 200 745.54 800 0.29 1.48 6.16 6.74 661.65 800 0.250 1.32 5.31 5.81

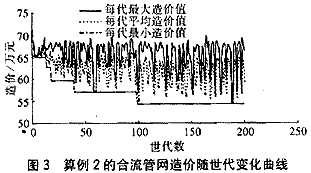
　　从表3可见，两种计算结果都满足合流制管渠设计计算的约束条件，但由于遗传算法选择了尽可能小的流速并采用了各种可行管径，结果使全长仅为2180m的管道埋深减小了0.93m。应用相同的造价函数，普通查图表法的工程造价为568778.35元，而遗传算法的工程造价为545014.15，可节约投资4.2%。其管网总造价随世代变化曲线见图3。

4　结论与建议

　　①引入可行管径集的概念，直接利用规格管径，分析了污水管道、雨水管渠和合流制管渠的遗传算法编码映射问题。其中，污水管道可行管径集是根据设计流量和最大设计充满度来确定的，而雨水管渠和合流制管渠可行管径集是根据直接优化法计算结果来确定的。从严格意义上来说，这里的可行管径集仅是实际可行管径集的一部分。
　　②通过实例进行了验证，计算结果表明该方法既能满足设计规范的要求，又可节约工程投资。
　　③在对污水管道系统设计计算中，建议可行管径采用4级管径；对于雨水管渠系统和合流制管渠系统，建议可行管径采用3级管径。对于陡坡或缓坡情况可适当调整。
　　④本文利用了常见重力流管道的水力计算公式进行分析，随着真空管道、压力管道以及各种新型管材的应用推广，在优化设计计算中应对可行管径集的计算及遗传算法的编码映射技巧不断完善和发展。

参考文献：

　　［1］张景国,李树平.遗传算法用于排水管道系统优化设计［J］.中国给水排水,1997,13(3):28-30.
　　［2］彭永臻,崔福义.给水排水工程计算机程序设计［M］.北京:中国建筑工业出版社,1994.
　　［3］孙慧修.排水工程［M］.北京：中国建筑工业出版社，1996.

　　电　　话：(021)63297006×2045
　　收稿日期：2002-04-05