工业动态用水定额数学模型
周广安
(青岛市节约用水办公室, 山东青岛 266001)
摘 要:工业生产用水受到多种因素影响,在制定用水定额时应充分考虑。通过建立“动态用水定额”数学模型,最后以曲线方程的形式表示企业产品用水定额,解决了企业产品结构、生产规模、用水水平和季节变化等因素对用水定额的影响问题。?
关键词:工业;动态用水定额;数学模型
中图分类号:TU991.4
文献标识码:C
文章编号:1000-4602(2002)06-0064-04
企业生产经营情况的变化必将影响用水量的变化,这就要求建立一种新的用水定额模型,充分考虑各种因素的影响,提高用水定额的应变能力。所谓动态用水定额数学模型,即是采用统计分析和水平衡测试相结合的方法,通过对各种影响用水的因素进行定性和定量分析,应用相关分析、回归分析、曲线拟合等理论方法,以计算机为辅助进行模拟计算,最后以曲线方程的形式表示用水定额,使得到的用水定额更加科学合理。?
1 动态用水定额
动态用水定额是相对静态用水定额而言的,是指某一用水过程在用水参数(影响因素)相对稳定的情况下具有固定的用水定额,但随着用水参数(影响因素)的改变,用水定额也同时随之做相应调整。?
1.1 工业用水定额的影响因素
企业生产用水受到多种因素的影响,如产品结构、产量、企业的技术管理水平、用水管理水平、生产设备状况、生产工艺、用水工艺、生产周期、季节(气温)变化、水质变化、原料质量、意外事故(如管道破裂漏水)等,如果对所有的影响因素分别进行单项分析计算就需要引入很多参数,在实际操作中是不可行的,因此必须先进行定性分析,将其中相似的项合并,然后再进行定量分析。
企业的技术管理水平、用水管理水平、生产设备状况、生产工艺、用水工艺等因素具有很大的相似性,基本上反映了企业的用水现状即用水技术管理水平;生产周期、季节(气温)变化、水质变化等因素是由市场或气候等引起的,主要反映为时间上的变化,可归纳为季节变化因素(很多企业是以月份为周期进行生产计划安排的,因此生产周期可与季节(月份)变化合并考虑。由于原料质量、意外事故等非稳定因素很难控制且不可预测,故在此不进行定量分析。
通过定性分析和归纳,影响企业产品用水定额的主要因素可压缩为4项:产品结构、生产规模、用水技术管理水平和季节变化。
为考察4项主要因素对用水定额的影响,引入了产品折算系数、产品产量、水的重复利用率、季节(月份)调节系数等4个参数,以便进行定量分析。由于水的重复利用率主要是由企业的用水技术管理水平决定的,因此用“水的重复利用率”这一参数来表示企业的用水技术管理水平。
在进行定量分析时应按以下先后顺序加以考虑:产品折算系数、季节(月份)调节系数、产品产量、水的重复利用率。?
1.2 动态用水定额的依据
据统计,大多数企业的单位产品取水量与产品产量、水的重复利用率之间均存在着负相关关系,即单位产品取水量随着产品产量的增加和水的重复利用率的提高而降低。这种关系的存在为动态用水定额的制定提供了理论和统计上的依据。?
2 建立数学模型
2.1 基础资料
① 最近3年各月的各种产品产量资料;
② 最近3年各月对应于各种产品产量的取水量资料;
③ 最近3年各月的用水量资料;
④ 最近一次的水平衡测试资料。?
2.2 产品折算系数
在实际生产中企业多是同时或周期性地生产多种产品。由于这些产品的用水常常混合在一起无法区分,所以要精确地计算出每一种产品的用水定额十分困难。为此,可以通过折算系数把次要产品产量折算为主要产品产量,求出主要产品的用水定额。次要产品用水定额可以用主要产品用水定额与该种次要产品折算系数之积来表示。
Zf=Wf/W
式中?Zf——第f种产品的折算系数
? Wf——第f种产品的单位产品取水量
? W——主要产品的单位产品取水量?
2.3 季节(月份) 调节系数
在其他条件不变或相对稳定的情况下,季节变化和相对稳定的生产周期变化对产品生产用水的影响是显而易见的,可利用季节(月份)调节系数对用水定额进行修正。
![]()
(i=1,2,…,12;j=1,2,…,m)?
式中?Ci——第i月的季节调节系数
? Wij——第j年第i月的统计单位产品取水量
? Wkj——第j年第k月的统计单位产品取水量
? k——水平衡测试所在月份
? m——统计样本的年数?
2.4 相关分析
① 单位产品取水量与产品产量的相关系数
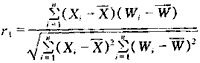
② 单位产品取水量与水的重复利用率的相关系数
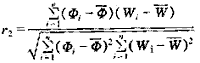
式中 ?Xi、Wi、Φi——第i个统计产品产量、单位产品取水量、重复利用率
2.5 回归分析
① 二元回归
假设W与X之间有如下关系:
? W=AXα+C?
采用最小二乘法来计算模型中的回归系数,令X=Xα,将二元非线性方程化为线性方程:
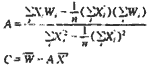
对所求得的回归方程进行显著性检验,
回归平方和:
![]()
总的偏差平方和:
![]()
剩余平方和:
SE=ST-SR
统计量:
? F=SR/[SE/(n-2)
在给定水平α下,当F>Fα(1,n-2)时回归方程W=AXα+C高度显著。
② 多元回归
假设W与X和Φ之间存有如下关系:
?W=AXα+BΦβ+C?
由于W与X以及W与Φ之间均为负相关关系,因此一般取α和β分别等于-1。?
令X=Xα,Φ=Φβ,获得线性方程W=AX′+BΦ′+C。
为了减小计算误差需进行“标准化”变换,令:
? X″i=[Xi′-X′]/σx
? Φ″i=Φ′i-Φ′/σΦ
? W′i=Wi-W/σW
其中:
? σx=(∑(X′i-X′)2)0.5
? σΦ=[(∑(Φ′i-Φ′)2]0.5
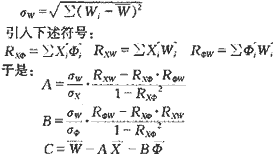
对多元回归方程进行显著性检验:
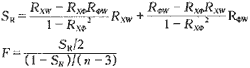
在给定水平α下若F>Fα(2,n-3)则多元回归方程显著。?
2.6 用水定额
① 基础定额
首先用数理统计法对历年用水资料进行统计分析。
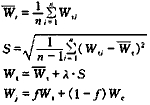
式中?Wti——第i个统计单位产品取水量(i=1,2,…,n)
? Wt——统计单位产品取水量
? Wc——测试单位产品取水量
? Wj——加权单位产品取水量
? n——统计数据的样本个数
? S——标准差
? λ——正态分布系数
? f——权重系数?
令 Xb=fXt+(1-f)Xc,Φb=fΦt+(1-f)Φc
式中 Xt、Xc——统计产品产量和测试产品产量
? Φt、Φc——统计重复利用率和测试重复利用率
求得:
? W′b=AXαb+BΦβb+C
〔r1<0,r2<0,|r1|>rα(n-2)且|r2|>rα(n-2)〕
W′b=AXαb+C
{r1<0,|r1|>rα(n-2)且〔|r2|<rα(n-2)或r2>0〕}
W′b=Wj〔r1>0或|r1|<rα(n-2)〕
取Wj和W′b的平均值作为企业用水的基础定额:
? Wb=1/2(Wj+W′b)
② 计划定额(动态用水定额)
引入系数K?
当r1<0、r2<0,|r1|>rα(n-2)、|r2|>rα( n-2)时,K=(AXα+BΦβ+C)/W′b。
当r1<0、|r1|>rα(n-2)且〔|r2|<rα(n-2)或r2<0〕时,K=(AXα+C)/W′b。
当r1>0或|r1|<rα(n-2)时,K=1。
则计划定额为:
? Wp=Ci·K·Wb?
2.7 工业产品的行业用水定额
同一行业中各企业的产品用水定额制定出来以后用以下公式求行业用水定额:
?WⅠ=WⅠ+λ·SⅠ?
式中 WⅠ——第Ⅰ类产品的行业用水定额
WⅠ——该行业各企业中第Ⅰ类产品的基础用水定额平均值
SⅠ——该行业各企业第Ⅰ类产品的基础用水定额的标准差
? λ——正态分布系数
3 应用实例
3.1 用水定额的制定
某单位用水定额—产品产量—重复利用率关系曲线见图1。
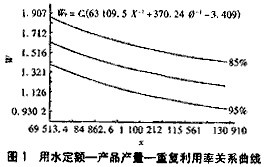
经计算,某工厂的基础用水定额Wb=1.453,12月的季节调节系数C12=0.959,计划定额方程系数K=43433.8X-1+254.81Φ-1-2.346。假如该厂12月生产计划Xp=100000,Φp=93%,则K=0.828,计划定额Wp=1.154。?
3.2 用水定额水平评定
该厂在1997年制定用水定额时的月生产规模约为74000,水的重复利用率约为91.5%,基础用水定额为1.453。2000年的生产及实际用水情况见表1。
计算公式 Wp=Ci·K·Wb
K=43 433.8X-1+254.81Φ-1-2.346?
从表1可以看出,2000年该单位的产品产量和水的重复利用率都有了较大提高,平均值分别达到94259和94.8%,实际单位产品取水量均值为1.266,比基础用水定额降低了12.87%。若用静态的基础用水定额Wb进行考核,则偏差很大(如2月实际产品产量达到148665,实际单位产品取水量为0.884;12月实际产品产量仅为31445,实际单位产品取水量为3.152,基础用水定额Wb与实际用水单耗相比差率分别达到64.32%和-53.9%),而如果考虑了产品产量和用水技术管理水平等因素的影响,用动态的计划用水定额Wb进行考核,则可以大大降低考核误差,使用水定额与实际用水情况更加吻合。
4 结语 ?
动态用水定额数学模型具有以下特点:
① 合理性
充分考虑了各种主要影响因素对用水定额的影响,并利用工业企业单位产品取水量与产品产量和水的重复利用率之间的关系建立曲线方程,根据不同的生产经营状况确定相应的用水定额,弥补了静态定额的缺陷;
② 先进性
引入正态分布系数λ,当λ=-0.67时P(λ)=25%,使统计单位产品取水量达到先进水平,而基础定额由水平衡测试、数理统计和回归分析等多种方法共同决定,其算法更加先进,在此基础上通过参数修正得到计划定额,更符合实际要求;
③ 实用性
只要提供最近3年每个月的各种产品产量、取水量、用水量和水平衡测试等资料,即可直接通过计算机进行分析计算和曲线模拟,既减轻了工作量,又提高了计算结果的准确性和直观性。
电 话:(0532)2792011
收稿日期:2001-10-17
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 [email protected] ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








