污水回用网络优化设计的研究

周兵，杜红彬，樊希山
（大连理工大学化工学院，辽宁 大连116012）

　　摘　要：在工业生产的各个用水过程中会产生大量污水，使污水最小化的一个有效的方法就是设计污水回用网络，以便使污水得到最大程度的回用，这样在满足用水要求的同时使新鲜水消耗最少。利用自适应模拟运大遗传算法对用水网络进行最优设计。
　　关键词：污水；污水回用；污水回用网络
　　中图分类号：TP31
　　文献标识码：A
　　文章编号：1009－2455（2002）03－0013－03

Study on the Optimum Design of Wastewater Reuse Network
ZHOU Bing, DU Hong-bin, FAN Xi-shan
(School of Chemical Engineering, Dalian University of Technology, Dalian 116012, China)

　　Abstract: A large amount of wastewater is produced in various processes in industries. A effective way to minimize wastewater is to design the wastewater reuse network so as to make maximal use of wastewater. Adaptive simulated annealing genetic algorithms is adopted for the optimum design of the wastewater network in this paper to meet the water demands as well as to minimize the fresh water consumption.
　　Key words: wastewater; wastewater reuse; wastewater reuse network

前言

　　在工业生产中，使污水最小化已成为人们普遍关心的问题，而污水最小化又等价于最小化新鲜水消耗。在此文中我们建立了污水回用网络，使之最大。程度的回用污水，并将我们所开发的自适应模拟退火遗传算法应用到此非线性规划问题，实现了用水网络的优化设计，所得的污水回用网络可使新鲜水消耗最少，同时满足用水要求。

1 污水回用网络模型[1]研究

1.1 污水回用网络（WWRN）
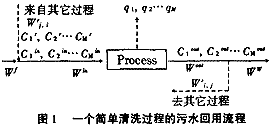
　　一个简单的清洗过程污水回用流程如图1所示。图中W_j为新鲜水流量，W^r_j，i为从过程i回用于过程j的污水流量，Ww为排出的污水量，q_i为清洗操作除去的杂质量。无数个这样的回用单元则构成了污水回用网络。
1.2 问题描述
　　在一个给定的、含有N个子过程、M种杂质（q_i,j,i∈N,j∈M）需除去的清洗过程中，对每一个子过程Pi，杂质的最大允许浓度（C_i，jⁱⁿ）_max和（Ci，j^out）_max是给定的。有必要设计这样一个最优的WWRN，即满足用水要求又使清洗消耗的新鲜水（W^f）最少。

1.3 优化模型
　　此优化模型可表示如下：

　　　　　

　　约束为：
①流股混合的质量守恒

　　　　　　

　　②流股分割的质量守恒

　　
　　在以上的表达中，若i=j则Wri，j表示内部循环流股，通常在无再生的情况上，内部循环流股设为0，若i≠j，Wri,j表示外部循环流股。其中，可能在第i级的操作中回用水就可满足用水要求，此时Wfi=0。此问题属非线性约束优化问题，下面简单介绍一下自适应模拟退火遗传算法，并用两个实例来说明使用此算法对用水网络进行最优设计。

2 自适应模拟退火遗传算法[2]（Adaptive SimulatedAnnealing Genetic Algorithms，ASAGA）

　　模拟退火遗传算法是将遗传算法[3--4]与模拟退火算法[5]相结合而构成的一种优化方法。遗传算法的局部搜索能力较差，但把握搜索过程总体的能力较强；而模拟退火算法具有较强的局部搜索能力，并能使搜索过程避免陷入局部最优解，但模拟退火算法对整个搜索空间的状况了解不多，不便于使搜索过程进入最有希望的搜索区域，从而使得模拟退火算法的运算效率不高。但如果将遗传算法与模拟退火算法相结合，则有可能开发出性能优良的新的全局搜索算法。我们用模拟退火算法作为算法结构主体，将遗传算法嵌入其内层结构，并采取了自适应改变交叉和变异概率策略和自适应调整搜索步长策略对混合遗传退火算法进行了改进，这样就使此混合算法既有较快的收敛速度又有避免陷入局部极值的能力。

3 实例分析

　　我们用上述混合算法对两个较简单的用水网络进行最优污水回用网络设计。
3.1 单杂质过程 表1 例1原始数据 过程 最大人口浓度C_in^max/(mg.L^-1) 最大出口浓度C_out^max/(mg.L^-1) 传质量/（kg.h^-1) 1 0 100 2.0 2 50 100 5.0 3 50 800 30.0 4 400 800 4.0

　　优化模型建立如下：
　　　minf(x)=X₁+X₂+X₃+X₄约束条件如下：
　　①流股混合的质量守恒
　　　　X₁ⁱⁿ=X₁+X₁₁+X₂₁+X₃₁+X₄₁X₂ⁱⁿ=X₂+X₁₂+X₂₂+X₃₂+X₄₂
　　　　X₃ⁱⁿ=X₃+X₁₃+X₂₃+X₃₃+X₄₃
　　　　x₄ⁱⁿ=X₄+X₁₄+X₂₄+X₃₄+X₄₄
　　②流股分割的质量守恒
　　　　X₁^out=W₁+X₁₁+X₁₂+X₁₃+X₁₄
　　　　X₂^out=W₂+X₂₁+X₂₂+X₂₃+X₂₄
　　　　X₃^out=W₃+X₃₁+X₃₂+X₃₃+X₃₄
　　　　X4^out=W₄+X₄₁+X₄₂+X₄₃+X₄₄
　　③每个子过程的组分质量守恒
　　　　C₁ⁱⁿX₁ⁱⁿ=C₁^outX₁₁+C₂^outX₂₁+C₃^outX₃₁+C₄^outX₄₁
　　　　C₂ⁱⁿX₂ⁱⁿ=C₁^outX₁₂+C₂^outX₂₂+C₃^outX₃₂+C₄^outX₄₂
　　　　C₃ⁱⁿX₃ⁱⁿ=C₁^outX₁₃+C₂^outX₂₃+C₃^outX₃₃+C₄^outX₄₃
　　　　C₄ⁱⁿX₄ⁱⁿ=C₁^outX₁₇+C₂^outX₂₄+C₃^outX₃₄+C₄^outX₄₄
　　　　q₁=X₁^outC₁^out-X₁ⁱⁿC₁ⁱⁿ
　　　　q₂=X₂^outC₂^out-X₂ⁱⁿC₂ⁱⁿ
　　　　q₃=X₃^outC₃^out-X₃ⁱⁿC₃ⁱⁿ
　　　　q₄=X₄^outC₄^out-X₄ⁱⁿC₄ⁱⁿ
　　④因为在此过程中除去的杂志量相对于水物流很小，可不计，故可认为：
　　　　Xⁱⁿi=X_i^out i=1,...4
　　将上述约束作为惩罚项。
　　另外，（C_iⁱⁿ）max≥C_iⁱⁿ≥0
　　　　　(C_i^out）max≥C_i^out≥0
　　　　　Xini≥0，Xi≥0，Xxj≥0, i=1,...4
　　包括在变量的上下界中了，不单独作为约束。
　　以上各式中符号说明如下：
　　minf(x)——最小新鲜水消耗量，t/h；
　　x_iⁱⁿ——过程入口流量，t/h；
　　X_i^out——过程出口流量，t/h；
　　X_i——各过程新鲜水消耗量，t/h；
　　W_i——各过程所排污水量，t/h；
　　C_iⁱⁿ——过程入口杂质浓度，mg/L；
　　Xij——i过程的污水回用于j过程的流量，t/h；
　　qi——清洗操作除出的杂质量，kg/h。
　　其中i=1,...4；j=1，...4。
　　把X_iⁱⁿ、X_i^out作为中间变量，将（1）代入（3），将（1）、（2）代入（4），经过化简，此问题变为32维，分别是Xi，Wi，C_iⁱⁿ，C_i^out，X_ij（i=1,...4,j=1,...4)。将变量的上下界确定在一个适当的范围内，对32个变量初始化后，利用ASAGA我们求得结果如表2。

表2 使用ASAGA所得结果 i Xi/(t.h^-1) W_i/(t.h^-1) C_iⁱⁿ/(mg.L^-1) C_i^out/(mg.L^-1) X_i,j/(t.h^-1) j 1 2 3 4 1 19.9736 0.0006 0 99.7342 0 0 19.9692 0 2 49.9741 44.2656 0.0058 99.8586 0 0 0.0042 5.7084 3 20.9262 40.8945 48.4857 781.8430 0 0 0 0 4 8.8818e^-16 5.7046 98.7657 798.9980 0 0 0 0

　　以上结果是数学上最优，在实际应用时还要进行处理，如太小的数可视为0，19.9736视为20等。由此用水网络可设计如图2所示。

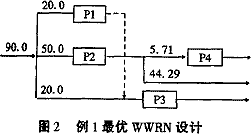
　　作为比较，表3列出了优化前后新鲜水的消耗量。

表3 新鲜水消耗量 过程 无回用 最优回用 1 20 20 2 50 50 3 37.5 20 4 5 0 新鲜水总量 112.5 90 新鲜水减少率 　 20%

3.2 多杂质过程
　　表4列出了实例2的限制组成数据，比例为两组分问题，取自文献[1]。

表4 例2原始数据 过程 组分 传质量/（kg.h^-1) C_in^max/(mg.L^-1) C_out^max/(mg.L^-1) 水流/(t.h^-1) 1 A 4 0 100 40 B 2 25 75 　 2 A 5.6 80 240 35 B 3.1 30 90 　

　　采用与例1同样的方法可得最优WWRN，如图3所示。

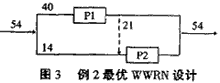
　　此过程共消耗新鲜水54t／h，如果每个操作都使用新鲜水则需63.4t／h，可见两者相比节水14.8％。

4 结论

　　在工业过程中，最优WWRN的设计往往是有效降低污水的关键。设计中的主要困难是在满足清洗任务的同时要使水流服得到最有效的分配。建立在优化基础上的设计方法可用来设计既节省费用又在结构上达到最优的污水回用网络。但有一点需说明，当流股和杂质组分太多时，最优解无法得到保证，这也正是我们需要进一步研究的工作。

参考文献：

　 ［1］Wang Y P and Smith R.Wastewater Minimization[J].Chem Eng Sci，1994，49（7）：981－1006.
　　[2] 杜红彬.基于遗传算法和模拟退火算法的混合算法的研究与应用［D］.大连：大连理工大学，1999.
　 ［3］刘勇，唐立山，陈屏.非数值并行算法—遗传算法［M］.北京：科学出版社，1998.
　　[4] 周明，孙树栋.遗传算法原理及应用［M］.北京：国防工业出版社，2000.
　　[5] 唐立山，谢云，尤矢勇，等.非数值并行算法——模拟退化算法[M].北京：科学出版社，1998.

---

　　作者简介：周兵（1977--），男，江苏江都人，硕士研究生，电话（0411）3609254，zhoubing1999＠263.net。