带因子—迭代法求解暴雨强度公式参数

任伯帜1，沈良峰1，许仕荣2，王涛2，谢社平2?
( 1.湘潭工学院土木工程系，湖南湘潭411201； 2.湖南大学土木工程学院，湖南长沙410082)

　　摘　要： 在修编长沙市暴雨强度公式的实践中，通过对现有各种求解城市暴雨强度公式参数的计算方法分析，提出应用带因子—迭代法求解。结果表明，该法不但较好地解决了非线性方程线性化时易出现的病态问题，而且放宽了迭代初始值的选择范围，迭代收敛性较好、求解过程稳定、拟合精度较高，实用可行。
　　关键词：城市排水；暴雨强度公式；带因子—迭代法；非线性方程；参数估计
　　中图分类号：TU823.6
　　文献标识码：C
　　文章编号：1000-4602(2002)02-0063-03

1 模型的建立

　　曲线拟合或科学试验中常见下列非线性方程组：?
　　fj(xj，yj，zj，…，ai)=0(i=1,2,3，…，m;j=1,2 ,3,…，N)　　　(1)?
　　其中fj(j=1,2,3,…，N)是m个参变量ai(i=1,2,3,…，m)的非线性函数。(xj,yj,zj)是通过N次试验观测所得的N组已知数据。在求解式(1)非线性方程组的参数ai时，常化为多元函数的极小值问题，即求与之等价的目标函数的极小值问题，从而确定参数ai：?

　　用矩阵与向量记号表示：X=［x1,x?2,x?3,…，xN］^T，Y=［y1,y2,y3,…，yN］^T?
　　　　　　　　　　　　　Z=［z1,z2,z3,…，zN］^T，A=［a1,a2,a3,…，am］^T
　　则有：F(X，Y，Z，A)=［f1(X,Y,Z,A),f2(X,Y,Z,A),f3(X,Y,Z,A),…，fN(X,Y,Z,A )］^T
　　则式(1)可改成：?
　　　　　V(X,Y,Z,A)=F(X,Y,Z,A)T?
　　　　　F(X,Y,Z,A)=‖F(X，Y，Z，A)‖²　　(3)?
　　为使式(2)、(3)有极小值，则需：

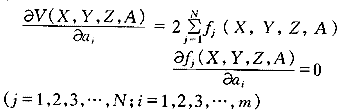
　　即有：V(X,Y,Z,A)=2DF(X,Y,Z,A)^T　　F(X,Y,Z,A)=0　　(4)

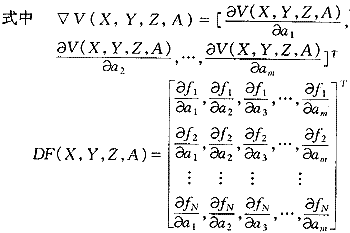
　　因F(X，Y，Z，A)是关于A的非线性函数，为此方程(4)是一个非线性方程组，一般难于直接求解，常采用逐次线性化处理。即设A0为解的初始近似值，ΔA为精确值与初始值之差，则有：A=A0+ΔA，将F(X，Y，Z，A)在A0附近Taylor展开，并略去ΔA的二次及二次以上各项得：?
　　F(X，Y，Z，A)=F(X,Y,Z,A0)+DF(X,Y,Z,A0)ΔA　　　　　(5)?
　　将式(5)代入式(3)，再由式(4)得：?
　　　　DF(X，Y，Z，A₀)T DF(X，Y，Z，A0) ?
　　　　ΔA+DF(X，Y，Z，A0)TF(X,Y, Z,A0)=0　　　　　　　(6)?
　　由于F(X，Y，Z，A)复杂的非线性，由Taylor展开线性化后得到的线性方程组易出现病态问题，给式(6)求解带来困难，为此引进阻尼因子u，从而增大［DF(X，Y，Z，A₀)TDF(X， Y，Z，A₀)］的主对角元素的值，则式(6)变为：?
　　DF(X，Y，Z，A₀)TDF(X，Y，Z，A₀)+uIm］ΔA+DF(X,Y,Z,A₀)T F(X，Y，Z，A₀)=0　　(7)?
　　式中Im——m×m阶单位矩阵?

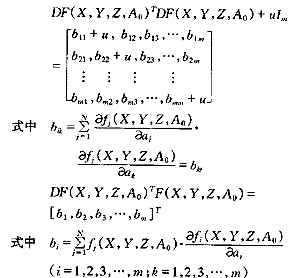
　　在迭代求解式(7)时，为放宽对初始值A0的选择，使迭代收敛或加速收敛，引入步长因子ω，即解方程组(7)得出的ΔA，不是直接由A=A₀+ΔA计算第一次近似值，而是把ΔA作为寻查方向，即改为：
A=A?0+ωΔA　　　　　　(8)?
　　其中步长因子ω的选择应满足：?
V(X，Y，Z，A?0+ωΔA)＜V(X，Y，Z，A?0)　　　　　(9)?
　　则由式(7)、(8)、(9)及求解参数的精度要求(max[DD(][]l≤i≤m[DD)]｜a_i-a_i⁽⁰⁾｜=max｜ΔA｜≤ε，其中ε为求解精度)构成了带因子—迭代法求解参数的数学模型。?

2　参数的求解

　　将i—t—p关系数据表中不同历时t和不同重现期p对应的不同雨强i组成N组(ij,tj,pj )已知数据组(j=1,2,3,…，N；N=9个历时×11个重现期=99)，则将城市暴雨强度公式变形得下列方程组：?

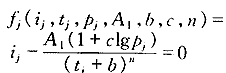
　　即：fj(ij,tj,pj,A1,b,c,n)=0(j=1,2,3,…，N)　　　　(10)?
　　式(10)中函数fj是关于4个参数(A1，b,c,n)的非线性函数，(ij,tj,pj)为N组已知数组。对函数fj中4个参数分别求导得：?

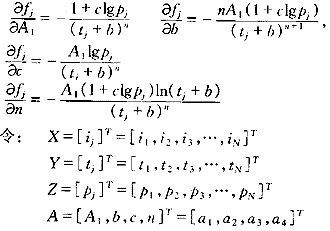
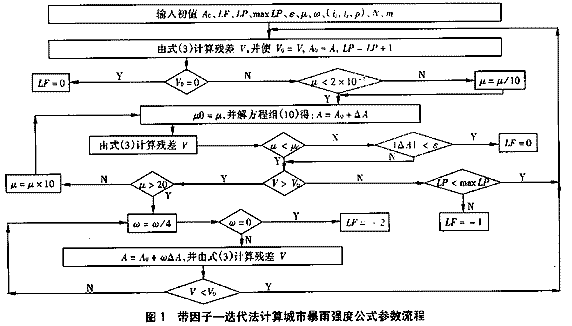
　　选择迭代初值A0，由带因子—迭代求参数模型按图1进行迭代求解。当max｜ΔA｜≤ε时，则输出待求参数A1、b、c、n。?
ε取值范围一般为10^-3～10^-5；μ初值赋为0.01；ω初值赋为1；已知数 据组总数N=99；m=4；迭代次数LP初值赋为零；输出参数LF=0表示计算成功并输出参数，LF= -1表示迭代次数大于假定的maxLP时仍未收敛，可再放大maxLP进行迭代，LF=-2表 示u=100、ω=0，无法迭代下去(可能是因为精度要求太高)，改变精度要求即可继续迭代。

3　应用实例

　　湖南省长沙市有连续25年(1974年—1998年)的雨量资料，每场暴雨取5、10、15、20、30、4 5、60、90、120min9个历时段的最大降雨强度，每年各历时取6个雨强最大值；不分年次先后按文献^［6］的从大到小排序，选取其中4倍年份数的前面样本作为统计的基础资料，按文献^［6］的计算方法得出长沙市的i—t—p关系数据，在此基础上推求暴雨公式参数。
　　通过各种方法的应用程序计算得出的长沙市暴雨强度公式参数结果对比见表1。 表1　不同方法对长沙市暴雨强度公式参数的计算结果对比 计 算 方法 暴雨强度公式参数 V A₁ b c n CRE编制法 11.511 12.643 0.385 0.654 0.3071 单纯加速法 11.782 12.730 0.389 0.665 0.2954 高斯—牛顿法 12.05 12.935 0.397 0.676 0.2641 迭代法 12.483 13.012 0.403 0.680 0.2336 麦夸尔特法 12.674 13.263 0.406 0.684 0.2053 带因子—迭代法 12.877 13.275 0.410 0.685 0.1459

　　从表1可知，在相同的i—t—p关系数据表及比较条件下，用带因子—迭代法推求城市暴雨强度公式参数优于其他方法，此法推求的长沙市暴雨强度公式为：?
?　i=[12.877(1+0.410 lgp)］/［(t+13.275)0.685］

4 结语

　　应用带因子—迭代法推求城市暴雨强度公式参数的结果表明该法是合理可行的，它具有如下特点：?
　　①较好地克服了非线性方程线性化时易出现的病态问题，使迭代求解过程稳定；?
　　②较好地解决了现有各种方法中迭代初始值选择的局限性，放宽了初始值的选择范围，且能做到迭代收敛或加速收敛；?
　　③应用实例表明该法优于现有各种方法，且精度满足现行规范的要求。

参考文献：

　　［1］GB 14—87，室外排水工程设计规范［S］.
　　［2］王世刚.城市暴雨公式参数优化计算程序［J］.中国给水排水，1987，3(4) ：50-52.
　　［3］张字贤.用高斯—迭代法求解暴雨强度公式参数［J］.河海大学学报，1995，23(5)：106-11 1.
　　［4］赵建国.迭代法求解暴雨强度公式参数［J］.给水排水，1997，23(12)：9- 12.
　　［5］李树平，刘遂庆，黄延林.用麦夸尔特法推求暴雨强度公式参数［J］.给水排水，1999，25( 2)：26-28.
　　［6］任伯帜，许仕荣，王涛.皮尔逊—Ⅲ型分布统计参数的确定［J］.中国给水排水，2001，17( 1)：40-42.

　　电　话：(0732)8290041?
　　收稿日期：2001-06-31