灰色—神经网络组合模型预测城市用水量

李斌1，许仕荣1，柏光明2，李黎武1?
( 1.湖南大学土木工程学院，湖南长沙410082； 2.长沙市自来水公司，湖南长沙410015)

　　摘　要： 针对城市用水量的预测，建立了以预测方法有效度为优化指标的求解组合预测权重系数的优化模型，并对灰色—神经网络的二元组合预测模型采用简化方法求解。该方法应用于长沙市河西供水系统的用水量短期预测，误差较小，能满足实际需要。
　　关键词：城市用水量；组合预测；近似最优解；灰色—神经网络
　　中图分类号：TU991.31
　　文献标识码：C
　　文章编号：1000-4602(2002)02-0066-03

　　城市用水量预测是进行城市建设规划、输配水系统优化调度的一项十分重要的前提工作，可分为中长期预测和短期预测。常用的预测方法有两类：一类是因果解释性预测方法，即假定用水量与另外几个独立的影响因素之间的因果关系，从而建立起预测变量与影响因素之间的关系模型，其代表性方法有多元线性回归法、多元非线性回归法、人工神经网络法等；另一类为历史数据法，它只依赖于被预测量的历史观测数据及观测模式，通过序列分析找出其顺序变化规律并外推出未来的值，其代表性方法有时间序列分析法、灰色预测法等。
　　然而城市用水量的变化是一个指标和影响因素繁多的复杂系统，对其系统结构及输入和输出的模拟、预测和调控采用单个预测模型或部分因素和指标仅能包含或体现该系统的局部，若采用多个不同的预测模型并加以适当的有效组合或多个变量的科学综合，则可以充分地利用各种信息达到提高预测精度的目的。

1　灰色—神经网络组合预测

　　时用水量预测采用了GM(1,1)灰色预测模型，它是只包含用水量一个变量的一阶微分方程构成的模型，该模型的主要特点是所需自变量个数和历史数据样本个数都比较少。
　　人工神经网络采用应用较广泛的反向传播BP模型，以天气状况、节假日情况、日最高温度和日最低温度作为影响因素，以时用水量作为其输出值，故BP网络的拓扑结构可确定为：4个输入层神经元、6个隐含层神经元和1个输出层神经元。
　　湖南大学谢德华的学位论文中给出了以上两种方法的数学模型及求解方法，在此基础上建立了两者的组合预测模型及其求解方法。
1.1　模型的建立
　　①预测方法有效度概念?
　　设yt(t=1,2,…,N)为实际值，fit为某一预测方法的预测值，Ait为fit在时刻t的预测精度(其中N为预测数据个数)，则：
?　　　　　Ait=1-｜(y_t-f_it)/yt｜　　　　　　(1)
　　由Ait构成预测方法fit的精度序列，该序列的均值与均方差分别为：

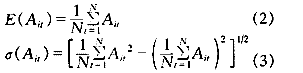
　　则预测方法fi的有效度指标定义为：
?　　　　Si=E(Ait)［1-σ(Ait)］　　　　(4)?
　　②组合预测优化模型?
　　以有效度为指标建立求解组合预测权系数k的优化模型。
　　设yt(t=1,2,…,N)为实际观测值；fit，…，fmt为m种预测方法的预测值；ki，…，km为各预测方法的加权系数；yt=k1f1t+k2f2t+…+kmfmt为组合预测方法的预测值；At为组合预测在t时刻的预测精度，则：

　　由式(4)可知，该组合预测的有效度指标为：?
?　　　　　　　S=E(At)·［1-σ(At)］　　　(6)?
　　因此S越大，说明该组合预测方法越有效，则以式(6)为目标函数，考虑加权系数的规范性约束，可以得如下的优化模型：

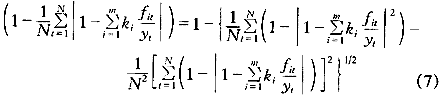
1.2　模型的近似最优解
　　模型中由于有绝对值的存在和权系数所在位置的分散，其求解十分复杂，当对城市用水量的预测用于输配水系统的实时调度时将很不实用。因此，必须加以简化，寻求一个近似最优解。
　　在只有两个预测方法组合的情况下，通过数学分析，可知At、E(At)、σ(At)与组合权系数k之间存在如下几个近似关系：
　　①组合预测精度At与组合权系数k的近似关系：
?　　　　　　　　At=kA_1t-(1-k)A_2t　　　(8)?
　　②组合预测精度序列均值E(At)与权系数k的近似关系：?
?　　　　　　　　E(At)=kE(A1t)+(1-k)E(A_2t)?　　　(9)?
　　③组合预测精度序列均方差σ(At)与权系数的近似关系为：?

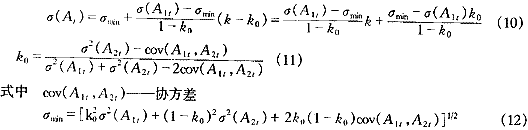
　　将式(9)、(10)代入优化模型(7)中得求解权系数近似解的简化模型为：

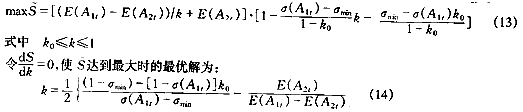
　　当由式(14)确定的k值不在［k0,1］之间时，应对其进行修正，设σ1、σ2分别为预测方法f1、f2与实际值的均方差，则有：
?　　k=k_修正=σ²/(σ1+σ²)　　　　(15)?
1.3　时用水量预测的简要步骤
　　①用灰色GM(1,1)模型和人工神经网络模型分别进行预测，得预测序列y1和y2；
　　②由式(2)、(3)计算E(y1)、E(y2)、σ(y1)、σ(y2) 及两个序列的协方差cov(y1,y2)；一般情况下两种预测方法是相互独立的，因此cov(y1,y2)=0；
　　③由式(11)、(12)求出k0、σmin；
　　④若k0=1，则k=1，转步骤⑤，否则转步骤⑥；
　　⑤计算组合预测值，输出预测值序列，结束计算；
　　⑥按式(14)、(15)求出权系数k，转步骤⑤。

2　应用实例

　　在长沙市自来水公司863/CIMS应用示范工程的管网调度系统中，运用了灰色—神经网络组合预测方法对河西区管网用水量进行短期预测。其中一组实测数据如表1。 表1　　实测时用水量　　　m³/h? 日期 时用水量 日期 时用水量 日期 时用水量 7月29日 5750.50 8月8日 5963.25 8月20日 5700.00 7月30日 5887.00 8月9日 5465.25 8月21日 5750.50 7月31日 5893.00 8月10日 5894.75 8月22日 5600.00 8月1日 5561.00 8月11日 5469.25 8月23日 5553.25 8月2日 5839.50 8月12日 5640.50 8月24日 5834.00 8月3日 5569.00 8月13日 5996.75 8月25日 5897.00 8月4日 5881.25 8月14日 5723.00 8月26日 5724.50 8月5日 6283.50 8月15日 5718.00 8月25日 5575.50 8月6日 5576.00 8月16日 5924.50 8月26日 5690.50 8月7日 5973.75 8月17月 5631.00 8月27日 5659.50

　　用表1中7月29日—8月12日的数据作为样本，对8月13日—8月27日8时～9时的时用水量用灰色方法、BP神经网络方法、灰色—神经网络组合预测方法分别进行预测，结果见表2。 其中组合预测中灰色预测的权系数为0.667，神经网络预测的权系数为0.333。 表2 时用水量预测结果 实际用水量(m³/h) 灰色预测 神经网络预测 组合预测 预测值(m³/h) 误差(%) 预测值(m³/h) 误差(%) 预测值(m³/h) 误差(%) 5996.75 5689.41 5.13 6100.00 -1.72 5826.10 2.84 5723.00 5777.53 -0.95 5963.00 -4.19 5839.28 -2.03 5718.00 5719.65 -0.029 6002.00 -4.97 5813.65 -1.67 5924.50 5718.10 3.48 6002.00 -1.31 5812.62 1.88 5631.00 5698.37 -1.20 5500.00 2.33 5632.33 -0.02 5700.00 5672.86 0.48 5500.00 3.51 5615.31 1.48 5750.50 5739.21 0.20 5500.00 4.35 5659.57 1.58 5600.00 5732.52 -2.37 5500.00 1.79 5655.11 -0.98 5553.25 5716.45 -2.94 5570.00 -0.29 5667.69 -2.06 5834.00 5692.11 2.43 5500.00 5.73 5628.15 3.52 5897.00 5767.27 2.20 5661.00 4.00 5731.89 2.79 5724.50 5790.34 -1.15 5793.00 -1.20 5791.23 -1.16 5575.50 5722.12 -2.63 5500.00 1.35 5648.17 -1.30 5690.50 5643.20 0.83 5500.00 3.35 5595.53 1.66 5659.50 5701.52 -0.74 5718.00 -1.04 5707.01 -0.83

　　为检验预测效果的好坏，按照整体评价预测方法的原则和惯例，采用以下指标来评价：?
①平均绝对误差?

　　式中　0≤U≤1，U→0精确度高，U→1精确度低
?　　　　yi——实际值
?　　　　——预测值
?　　　　n——预测数据个数
　　评价结果见表3。 表3　预测效果评价表 预测方法 MAE MAPE U 有效度(S) 灰色预测 102.99 0.0178 0.0114 0.9688 神经网络预测 157.73 0.0274 0.0160 0.9570 组合预测 99.58 0.0173 0.0097 0.9744

　　由表3可知，灰色—神经网络组合预测的三项指标全部优于灰色预测和神经网络预测，充分显示了该方法的优势；且表2中组合预测的单个预测值误差也完全达到了城市供水调度所需的工程精度，表明组合预测适用于生产实际。

参考文献：

　　 ［1］许仕荣.配水系统优化调度［J］.湖南大学学报，1998,25(6)：86-91.
［2］ 马永开，唐小我.线性组合预测模型优化问题研究［J］.系统工程理论与实践，1998，18(9 )：110-114.
［3］马永开，唐小我.多目标组合预测优化模型研究［J］.统计研究，1997，(4) ：45-48.
［4］ 董景荣.一种新的基于模糊模型的非线性组合预测方法及其应用［J］.系统工程理论与实践，2000，20(5)：109-144.
［5］ 王明涛.确定组合预测权系数最优近似解的方法研究［J］.系统工程理论与实践，2000，20(3)：104-109.

　　电　　话：013517314267?
　　收稿日期：2001-06-17