移动罩滤池水力计算的理论研究
| 论文类型 | 技术与工程 | 发表日期 | 2001-11-01 |
| 作者 | 戚盛豪 | ||
| 摘要 | 本文从过滤水力学的观点出发,分析和研究了移动罩滤池各滤格间的滤速变迁和水头损失变化规律,推导出滤格的最高滤速与平均滤速(也就是移动罩滤池的设计滤速)的比例关系以及期终水头损失的计算方法。为了验证研究分析的结果,又在南市水厂进行了模拟试验测定,与理论计算进行比较,从而提出了实用的计算方法。此外,基于理论分析和测定,还结合几年来设计实践经验,对移动罩滤池的进、出水布置以及反冲洗计算原则提出了看法,供设计时参考。最后,还提出了一些尚待解决的问题,供水力学研究者进一步研究。 | ||
戚盛豪
本文从过滤水力学的观点出发,分析和研究了移动罩滤池各滤格间的滤速变迁和水头损失变化规律,推导出滤格的最高滤速与平均滤速(也就是移动罩滤池的设计滤速)的比例关系以及期终水头损失的计算方法。为了验证研究分析的结果,又在南市水厂进行了模拟试验测定,与理论计算进行比较,从而提出了实用的计算方法。
此外,基于理论分析和测定,还结合几年来设计实践经验,对移动罩滤池的进、出水布置以及反冲洗计算原则提出了看法,供设计时参考。最后,还提出了一些尚待解决的问题,供水力学研究者进一步研究。
移动罩滤池水力计算的理论研究
近几年来随着给水事业的发展,在给水处理中出现了许多新的净水设备,提高了净化效率,改进了操作管理。移动罩滤池就是近年来初步试验成功的新型过滤设备。由于它具有结构简单、投资省、操作方便,引起了设计与使用方面.的重视。但几年来对于移动罩滤池的研究大致偏重于罩体的机械设计和冲洗的自动化方法等几个方面,对于移动罩滤池的设计理论尚未见有报导。现将决定移动罩滤池设计的水力因素及反冲洗设备的理论分析提搞肤浅的看法供讨论。
一、移动罩滤池的水力因素
1.滤速的变化
移动罩滤池是由若干滤格组成,并设有公共进水和公共出水系统的滤池,每滤格均在相同的水位差,以阶梯式进行降速过滤运行。而整个滤池又以恒定的水量进行工作。滤池布置见图—1;沉淀水①进入滤池后,通过砂层和支承层②,进入集水区③,通过出水虹吸管,最后从出水堰⑤流入清水池。由于移动罩滤池结构上的限制,不象普通快滤池那样,可用阻流装置或闸门以调节各格滤池内的滤速。
根据过滤理论的一般概念,可列出各滤格的水头损失表达式,如下:
b1m=b1′+h1″
h2m=h2′+h2″
...=......
him=hi′+hi″
式中 him——i号滤格水头损失
hi′——i号滤格清洁滤料的层流损失和集水系统的紊流损失。
hi″——i号滤格滤料沾污后增加的水头损失。
由于各滤格的进出水均连通,故水位是一致的,即
h1m=h2m=...=him=h1′+h1″=h2′+h2″=......

当1号滤格冲洗结束,开始过滤时滤料是清洁的。h1″等于零,h1′为滤料给定级配下的水头损失;即h1m=h1′,也就是图1中,滤池水位L0与虹吸管水位L1之差(△h)。如果集水系统中的紊流损失忽略不计,则1号滤格清洁滤层的水头损失h1′(即△h)可用有关公式进行计算。在该瞬向,2号,3号………滤格是沾污的,h2″,h3″...就不等于零,其大小取决于该滤格的过滤时间,即沾污程度,进水浊度以及滤料颗粒形状等。在给定的滤料级配和进水浊度时h2″......h1″仅与滤格滤层沾污程度有关,应为过滤时间,滤速的函数。所以当1号滤格反冲洗结束投入运转时,各滤格的水头损失可写成如下的通用公式:
h1′=h2′+f(t2,v2)=h1′+f(t3,v3)=h1′+f(ti,vi)……(1)
式中 ti,vi各为i号滤格的运行时间和瞬时滤速。
随着过滤的进行,1号滤格以及其他滤格的沾污程度逐渐增加,水头损失△h逐渐增加,虹吸管中的水位从L1,逐渐下降到L2。在这阶段,如普通虹吸滤池那样,基本上是变水头条件下的恒速过滤性状,(实际上,各滤格的滤速也略有升,降;但因变化较小,可忽略不计)。各滤格在大致恒定的滤速下工作。1号滤格滤速值最大,其他各滤格的滤速根据其积污程度地低于1号滤格。当2号滤格到最大沾污量(滤速最小)时,水位相应下降到L2就开始反冲洗。反冲洗结束投入运行时水位又恢复到L1,1号滤格的滤速,由于滤格内滤料已有一定的沾污,就降低到另一个恒定滤速。(1号滤格在一个周期中的滤速变化示于图2),其他各滤格的滤速也相应地降低一级,而2号滤格的滤速则达到最大值。如果移动罩滤池由4滤格组成,则4滤格的滤速变化曲线可得如图——3所示的带状曲线,平均滤速界于两极限之间。换言之,在一个周期内,总有滤格在最高恒定滤速下运行,也总有滤格在最低恒定滤速下运行。

2.期初与期终水头损失,最高滤速的分析
我们仍用4滤格的移动罩滤池为例。在每一周期中,如图-1中虹吸管的水位从L2变化到L1及从L1变化到L2共发生四次如图4(a)中的曲线。C′点相当于水位L1而D′点相当于水位L2,B′点是1号滤格冲洗前的水位,也应为L2。图4(b)是1号滤格在一个周期中的变化已如前述。当1号滤格停止工作,进水量将在其他滤格中重新分配,滤速略有增加,故水位L2略有降低,(见图4(a)中曲线的向下突出部分)。一旦冲洗结束,开始投入运转时,水位即从L2上升到L1。当水位达到L3时,1号滤格的滤速开始达到C点,在C点时的滤速称为最高滤速Vmax,而在B点的滤速称为最低滤速Vmin,平均滤速为Vav,各滤格的滤速分布计算如下:

为简化计算,由积污增加的水头损失假定近似正比于滤速与运行时间①,公式(1)中的h1′,h2′.....等于K1、V1,k1v2......(k1为渗透系数,v1,v2为各滤格的滤速。f(t2v2),f(t3v3),...等于k2v2t2,k2v3t3...(k2为比例常数,t2,t3...为相应滤格的运转时间)。
公式(1)可写成:
k1v1=k1v2+k2v2t2=k1v2+k2v2(T/n)=k1v3=k2v3t3=k1v3+k2v3(2T/n)=k1v4+k2v4t4=k1v4+k2v4(3T/n)=......
(式中T为总周期,n=滤格数)
将上述各式相除,得

考虑到在实际运行中各滤格的滤料级配和厚度,以及其管道阻力均不可能完全一样,因而某滤格的最高滤速与平均滤速的比值辽可能比理论计算值大。为此,设计采用的K值应乘以一个系数。建议该系数采用1.2~1.5。
k2可通过现有水厂或中间试验得出的过滤周期结束时的水头损失和恒速过滤的滤速值,按下式计算;
k2=期终水头损失-期初水头损失/[周期(T)×滤速(V)] (3)
如果将图4(a)中的水位变化转换成水头损失与时间的关系曲线见图5根据C1leasby和Bernardo 1980年的研究②指出,如果有一座恒速滤池以Vav的恒定滤速运行,则其水头损失与时间的关系曲线应如图—5上的A—B,A—B的斜率基本上相似于ab的斜率。他们认为:“两种系统均在相同的平均滤速下运行,因而单位时间内的积污量是相等的”,所以两种系统的斜率也相同。OA为清洁滤料的水头损失,Bc为可利用的水头损失,用△H恒代表,bc为移动罩滤池可利用的水头损失用△H代表。因△ABC~△abc,
则AC/ac=BC/bc,ac=T/n(T为周期,n为滤格数)。
则T/(T/n)=△H恒/△H,△H=△H恒/n ......(4)
非常明显,移动罩滤池虹吸管中的最高水位L1应等于滤池水位L0减去清洁滤格在Vmax时的水头损失,而最低水位L2应等于L0-(L1+△H)。
汇总上面分析,移动罩滤池Vmax和期终水头损失的计算如下步骤:
1、在给定的滤料级配及厚度下,以Vav作为恒定滤速,进行恒速过滤的中间试验,求出清洁滤料的渗透系数k1,如无条件进行中间试验,则可用Blake—Kozθny③公式求出k1。
2.从恒速过滤的中间试验,求出期终可利用的水头损失及其相应的周期。如无条件进行中间试验,则可参照现有水厂的经验,决定恒速过滤可利用的水头损失和周期。用公式(3)及(2)、(2a),求出k2和α及v1、v2、……,由此即可求出最高滤速与平均滤速的关系:Vmax=v1=KVav。
3、用公式(4)求出△H,移动罩滤池期终水头损失H=Kk1Vav+△H

3、虹吸式反冲洗的水位计算
图-6为虹吸式移动罩滤池反冲洗设备布置示意图。上面已经谈到,当水位下降到L2时就开始反冲洗。反冲洗的水量来自相邻的滤格出水,而虹吸作用的动力则来自L2与集水井水位E之差,示於图-6。当制水量大于冲洗水量时,L2总比水位D高,故设计时采用D与E之水位差是偏安全的。
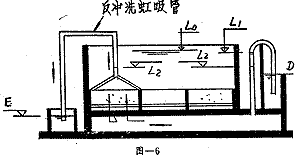
二、移动罩滤池模拟试验研究
为了验证第一节中所提出的K值和期终水头损失的计算。我们在南市水厂进行了模拟试验。试验设备是由四只¢150毫米有机玻璃滤格所组成。四只滤格的出水管均接在一根公共的出水总管上;各滤格及出水总管上均装了转子流量计(型号ZJ--25)及水头损失仪,以测定各滤格出水量和水头损失的变化。各滤格的出水管上又装设了取样龙头,测定水质浊度变化情况;为平衡及稳定备滤格的进水水位,各滤格离砂面1.7m处,设有溢流管,使多余水量流走。进水取自南市水厂“新高池”沉淀水。沉淀采用聚合铝作混凝剂,加注量约10mg/l,出水浊度6—7度,各滤格的滤料均采用快滤池黄砂,粒径为0.5—1.0mm,厚度为70cm。设备布置见图--7图--8。

1.试验方法和内容
试验自1984年3月12日至3月23日结束。分两阶段进行;第—阶段是进行移动罩滤池的模拟运行。采用的数据如下:滤速10m/h和12m/h两种,过滤周期14小时(因限于人大量沉淀水引入滤格,不论在任何情况下,有一定的水量从溢流管中流走,以保持水位恒定,调节出水总管上的闸门,使转子流量计的读数维持在70%(相应于移动罩滤池的平为10m/h)。因选取周期为14小时。故每隔3.5小时就有一滤格进行反冲洗,如此反复共进行28小时。随后,再进行平均滤速12米/时的模拟运行一个周期14小时。每小时测定流量,水质及水头损失。
第二阶段是进行各滤格的恒速过滤测定。采用的滤速也是10m/h和12m/h时各滤格滤速的变化。将两滤格以10m/h的恒定滤速下过滤,另两滤格以12m/h的恒定滤速下运行。每一小时测定其水头损失变化。
2、测定资料和分析计算
图-9和图-10各为平均滤速10m/h和12m/h时各滤格滤速的变化。从图可见,各滤格的滤速变化均呈阶梯形与理论曲线(见图-3及图-4)相似。最高滤速为24m/h——20m/h(及26m/h——23m/h);为平均滤速的
24/10=2.4至20/10=2.0倍;及26/12=2.2至23/12=1.9倍
图-11为平均滤速10m/h,水头损失、出水浊度与时间的关系曲线。图-12为平均滤速12为平均滤速12m/h时水头损失与时间的关系曲线。从图可见,曲线呈锯齿形与理论曲线(见图-5)相似。锯齿形曲线的最高与最低点的距离为移动罩滤池可利用的水头损失,已如前述。


为了计算k1,我们又测定了清洁滤料在不同滤速下的水头损失见下表:
水头损失(米) 滤速(米/时) k1 0.25 9.7 0.026 -- 12.0 0.0256 0.40 13.5 0.029 0.70 28.4 0.025 1.04 38.6 0.027 平均0.0268
图-13为恒速过滤水头损失与时间的关系曲线,由于南市水厂“新高池”在试验滤池运转10小时,进水水质下降到1度以下,迫使试验终止。为了弥补上述缺点,现将“净水工艺动态模拟试验研究”上的测定资料绘成如图-14的曲线供比较④。图-13~-14上曲线的斜率基本上与图-11~-12的斜率相似。现以滤速12米/时为例。从公式-3求:
k2=(1.4-0.30)/(14×12)=0.0066
从公式(2)(2a)求得:
α2=0.0256/(0.0256+0.0066(14/4)=0.532
α3=0.36
α4=0.27
v1(1+0.532+0.36+0.27)/4=12米/时
故;v1=22米/时
考虑到其他不利因素,取v1=1.22×22=26.4米/时,则
K=26.4/12=2.2(与测定相符)
从公式(4)得△H=(1.4-0.30)/4=0.27米
移动罩滤池的期终水头损失
H=Kk1Vav+△H=2.2×0.0256×12+0.27=0.95m
与图-12相似。

在模拟试验的同时,还测定了滤后水的总浊度变化,见图-11。在整个过滤过程中,滤后水浊度是比较稳定的,一般在1~3mg/l,过滤效果为75%~84%(进水浊度12~6.4mg/l)。
通过对各滤格在最高滤速时的浊度测定——运转三个周期共42个小时,每小时取样一次共42个水样,得出如下表的分析结果:
三、移动罩滤池进出水布置
1.进水布置
在大中型水厂中,为了检修及运转调度方便,移动罩滤池分成二组以上,因而在设计上必需考虑到各组水量的均匀分配问题。另外还有一个问题必需在设计时考虑,就是水厂的出水量随着季节的变化而变化。所以在计算时也应考虑小水量时,进出水位的变化情况。最简单的均分流量的方法是堰板,如图--1所示,或可在滤池纵方向上设置穿孔进水槽。这种进水槽既可保持滤池恒定进水位,又可防止进水对砂层的冲刷(见图--15)。

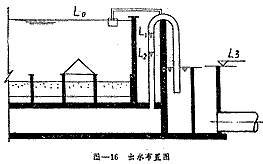
2.出水布置
图--16为移动罩滤池出水布置图。前面已经提及,在过滤进行中,虹吸管中的水位在L1与L2之间变化着。但出水堰L3的标高是固定的,这样会导致移动罩滤池总出水量波动很大,影响水质。为了弥补这个缺点,一般在虹吸管顶端装设水位稳定器。其作用原理是:当水位为L2时,水位稳定器不进气。当L2上升到L1时,如果虹吸管不采取措施,L0会下降(因出水水位差增加,出水量将相应增大),故此时打开浮筒上的进气阀,空气进入虹吸管, 增加虹吸管中的阻力,降低出水量(阻力值应等于L2-L1),以保持L0不变。
五、几点看法
1.上面的分析是基于各滤格在一个周期中等时间间隔进行冲洗的。这样,各滤格中的积污程度比较均匀。移动罩滤池需要的可利用水头损失约为恒速滤池可利用水头损失的1/n(n为滤格数)。如果移动罩滤池在周期开始时,就一次冲完所有滤格,运转到予定的周期结束, 再重复冲完所有滤格,这种方式的最大运行滤速将显著增加,从而影响出水水质,其期终水 头损失也比前者为大,故我们认为后者的冲洗方法是不予推荐的。
2.为使移动罩滤池的期终水头损失减小,从理论上讲分格数愈多愈好,但不应超过各滤格轮流冲洗一次所需的总周期。然而损失的减小呈等比级数形式,故增加过多,水头损失减少并不显著。在设计上应采用多少分格数,应由设计者结合水厂规模,工程造价,通过比较选定。
3.当滤格数较少时,由淤L2的变化较大,因而需设置出水虹吸管及其水位稳定器。但当滤格较多(>20)时,L2变化较小,则其水位稳定器的作用就显见降低或成为无必要了,(对于进水量变化导致水位的变化,则是另一问题了)。实践证明;在大型移动罩滤池中(如长桥水厂,杭州赤山埠水厂和南市水厂北部),移动罩滤池的水位稳定器,因没有发挥作用,有的巳拆除,有的则没有安装。
4.从第三(二)节的分析,可利用的水头损失代表着出水虹吸管的水位变幅,而出水虹吸管印的水位变化是决定水位稳定器进气量的依据。关于稳定器的计算是非常复什的,有待行进一步的研究。
5.为避免滤床中的气阻现象⑤,滤床上面的淹没深度应大于期终水头损失。从上面的计算,移动罩滤池的期终水头损失比普通快滤池小,所以其淹没深度也可比快滤池小,本文在编写和测试过程中得到叶正中工程师的帮助,在这里深表感谢。
参考文献
①移动冲洗罩滤池过滤水力计算探讨 戚盛豪 1982年9月(未发表)
②Declining-Rate Versus Constant-Rate Filtration, Bernardo and Cleasby;Journal of Enviromental Engineering Division, 1980, Dec.
③Water and Wast Water Treatment, Calculation and Chemistry and Physical Processes, Michael J.Humenick, Jr.Marcel Dekker, Inc.
④净水工艺动态模拟试验研究 上海市政工程设计院 1983年3月
⑤Water Clarification Processes,Herbert Hudsen, Van Nestrand Reinhold Company,1981
⑥Hydraulic Consideration in Declining-Rate Filtration, Cleasby and Bern-ardo, Journal of Enviromental Engineering Division, Dec.1980
⑦Deep Bed Filtration: Theory and Practice, K.J.Ives; Filtration and Separation Vol. 17 No.2,Mar/Apr. 1980
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 [email protected] ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








