改性滤料过滤除铁过程中水头损失增长的规律

邓慧萍 严煦世
（同济大学环境科学与工程学院 上海 200092 ）

　　摘　要：本文对改性游料过滤除铁过程中水头损失的变化规律进行了研究，得出厂水头损失的计算公式，并通过实验进行了验证。
　　关键词：改性滤料 过滤除铁 水头损失

The Increase of Loss Head in the Process of Iron
Removal though Filtration with Coated-media
Deng Huiping　　Yan Xushi
(School of Environmental Science & Technology Engineering of Tongji University SHANGHAI 200092)

　　Abstract:Inthis paper,an investigation on the regularities for the increase of loss head in the process of iron removal through filtration with coated-media is carried out, and a formula for calculating loss head is obtained anf verified by the experimental data.
　　Key words:coated-media, removal of iron through filtration, loss head

　　随着人们对用水量要求的日益增加，我国和世界上的许多城镇都以地下水作为水源。但地下水中常含有过量的铁和锰，需经处理才能满足生活饮用水和工业用水的要求，所以地下水除铁是地下水资源开发利用中的重要课题之一。目前在这一领域内最重要的课题是如何强化除铁工艺过程，改善初期水的水质和缩短滤料的成熟期。
　　实验研究表明^[1]：在过滤除铁过程中，使用改性滤料是改善滤料成熟前出水水质，缩短成熟期的有效方法之一。本文研究的目的，是对改性滤料过滤除铁过程个水头损失的变化规律进行研究，以得到水头损失的计算公式，并以实验数据进行验证。

1 改性滤料过滤除铁过程中水头损失的变化规律

　　在改性滤料过滤除铁过程中，滤层中氢氧化铁沉淀的形成和分布规律与一般用于水的澄清滤池中沉淀的分布情况是不同的。
　　在改性滤料过滤除铁过程中，滤层中形成的氢氧化物沉淀改变了过水断向和孔隙的几何结合。除铁过程的动力学理论表明，随着滤层中氢氧化合物的形成，增人了其比表面积，导致了水头损失的增加，即在沉淀物积累的过程中，滤料层的水流阻力发生变化，水头损失增加。
　　在滤池工作的任何时刻，其水头损失值可以分为二个部分：初始水头损失h₀和水头损失的增量△h。在除铁滤池中，初期水头损失和用于水的澄清滤池相同，可以用卡曼-康采尼（Carman-Kozony）公式表示:
　　
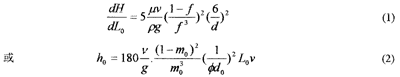
　　在改性滤料过滤除铁过程中，水头损失的增长规律不同于水的澄清过程。水头损失的增长与滤层的厚度有关，但是，如果滤层足够厚，使出水的含铁量随着滤层的增厚而不再变化，那么这时水头损失的增加将与滤层厚度无关^[1]。在这种情况下，水头损失的增加只取决于沉淀物在滤层中的分布情况，这种分布是随时间而变化的。
　　由改性滤料过滤除铁的动力学过程可以得到，从滤池开始工作经dt时段，在单位滤层表面沉积的氢氧化铁化合物的量为(C₀v/k₀)dt ^[2]。
　　根据过滤除铁的动力学理论和沉积物在滤层中的淤积情况，可以认为，滤层中水头损失的增加与沉积物量、水的粘滞系数、滤料颗粒的比表面积（粒径和孔隙率）成正比，与水的密度成反比，即

　　dh＝(K_pC₀S₀vμ/k₀ρ)dt　　　　　　(3)

　　式中：C₀－水中总的含铁量，mg/l；
　　　　　k₀－滤层中Fe3+的氧化速率常数，g·cm/h;
　　　　　V－滤速，m/h；
　　　　　t－过滤时间，h；
　　　　　ρ－水的密度，g/cm3；
　　　　　K_p－量纲系数，Kp=1/3000=0.000287；
　　　　　S₀－滤料颗粒的比表面积，l/cm.g；
　　　　　μ－水的动力粘滞系数，g/cm.s；
　　　　　h－滤层中水头损失的增长，m水柱；
　　在过滤除铁过程中，滤层中所形成的氢氧化铁沉淀是多孔介质，氢氧化铁的颗粒形状随着压力的变化而改变，颗粒压缩后，氢氧化铁沉淀的孔隙率减小，随着沉淀物的密实，对水流的阻力增加。
　　考虑到这些因素。在方程(3)中引人孔隙率系数和氢氧化铁沉淀的比阻，这二个参数反映了沉淀物的密实程度，式(3)可以表示为：

　　dh＝(K_pK_nC₀S₀vμγ/k₀ρ)dt　　　　　　(4)

　　式中：Kn－所形成的氢氧化铁沉淀的孔隙率系数；
　　　　　γ－氢氧化铁沉淀的比阻；
　　根据资料^[3]，氢氧化铁沉淀的孔隙率为0.586－0.644，平均值为0.615，那么氢氧化铁沉淀的孔隙率系数为

　　Kn=m＇/(1-m＇)=0.615/(1-0.615)=1.6　　　　　(5)

　　在滤层中所形成的氢氧化铁沉淀的比阻，可以按下列公式确定^[4]：
　　　　γ=b₀+a₀h^n₀　　　　　　　　　　　　　　　　(6)
　　式中：b₀、a₀、n₀－常数，由实验确定；
　　　　　h－滤层中的压力差，m水柱；
　　根据资料^[4]，a₀、n₀通常近似于1，所以式(6)可以表示为
　　　　　γ＝b₀＋h　　　　　　　　　　　　　　　　(7)
　　随着滤层中压差的增大，沉淀物的压实也就越快，式(7)表明，在压实过程中，除压差h外，同时还有其它力起作用，这些力以特征值 b₀表示，在γ＝f(h)的关系中，假定 h=0，得到了沉淀物的阻力为b₀值，即γ＝b₀。
　　当压力差h=0时，氢氧化铁沉淀的比阻力1，所以b₀=1。因为这一值的大小是不随水头损失的增加而变化。所以氢氧化铁沉淀的比阻可表示为
　　　　　γ=1＋h　　　　　　　　　　　　　　　　　(8)
　　将式(8)和系数K_p、K_n代入方程(4)，得

　　dh/(1+h)＝(0.00046C₀S₀vμ/ρk₀)dt　　　　　　(9)

　　对式(9)进行积分，得到

　　ln(1+h)=(0.00046C₀S₀vμ/ρk₀)t+q　　　　　　(10)

　　式中：q－积分常数；
　　当t=0时，h=0，得q=ln1　即q=0。
　　由此可以得到，计算除铁滤池滤层任何时刻的水头损失值的表达式为

　　

　　式(11)适用于德层厚度足以完成陈铁过程的情况。而除铁滤池的厚度可由除铁过程初始条件c=c0e^{(k₀s₀/v)L}得到：

　　L=v(lnC₀-lnC)/k₀S₀　　　　　(12)

　　如果实际滤层的厚度小于上述计算值，则必须考虑滤层厚度的因素，引入比例系数N：

　　N=L_x/L　　　　　(13)

　　式中：Lx－滤层的实际厚度，m。
　　这时水头损失增量的计算公式为

　　　　　　　(14)

　　在滤池工作的任何时刻t，滤层的水头损失为

　　

　　将滤层最大允许水头损失值H_max代人式(15)，可以计算出滤池的工作周期

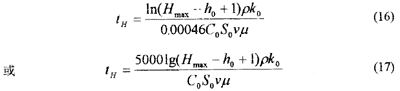
　　式(17)即为计算滤池工作周期的表达式。

2 实验结果

　　根据改性滤料过滤除铁的动力学理论，随着过滤过程的进行，氢氧化铁化合物在滤层中沉积使出水水质不断改善。所以，滤池的工作周期是由水头损失的极限值确定的，即水头损失是控制滤池工作周期的指标。为此，对不同粒径的滤料在不同滤速下的水头损失变化情况进行了研究，并对理论计算公式与实验结果进行了比较。
　　这组实验是在截曲尺寸为30×36mm，滤层厚度为360mm的滤柱中进行的，滤料为表面带有MnO.Fe₂O₃催化膜的陶粒滤料。
　　为了计算出除铁滤池中水头损失增长的规律，首先必须通过实验计算出Fe²⁺氧化速率常数k₀值，Fe²⁺氧化速率常数k₀可根据改性滤料过滤除铁动力学微分方程的初始条件，即ln(C₀/C)=K₀(S₀/v)L，通过实验确定^[2]。
　　在实验室的条件下进行实验，对于清洁滤层(t=0．己知原水中Fe²⁺浓度为C₀，对于某一滤层，在一定的工况条件下，可以测定出水中Fe²⁺浓度，己知滤速v和滤层厚度x，在单对数座标纸上，以ln(C₀/C)为横座标，L为纵座标，可以得到一条通过原点的直线，直线的斜率为K₀(S₀/v)，由此可以得到k₀值。
　　实验中选用了三种不同粒径的滤料，二种粒径分别为 0.2－1.0mm、2.0－3.5mm、3.5－5.0mm。原水中Fe²⁺浓度为2.64mg/l，水温为10℃，这时水的动力粘滞系数为0.0131g/cm.s，滤速分别为8m/h、10m/h、15m/h。实验条件和计算结果见表1和图1。

表1.确定k₀的实验条件和结果 序号 d(mm) S₀(cm-1) C₀(mg/l) v(m/h) K₀(S₀/v)L k₀ 工况1 2.0-3.5 34.02 2.64 8 5.188 1.22 工况2 2.0-3.5 34.02 2.64 10 4.024 1.183 工况3 2.0-3.5 34.02 2.64 15 1.862 0.821 工况4 3.5-5.0 21.71 2.64 8 2.849 1.05 工况5 0.2-1.0 168.89 2.64 8 30.61 1.45

　　在单对数座标纸上，以lnC₀-lnC为横座标，L为纵座标，应该得到一条斜率为K₀(S₀/v)的直线，见图1。

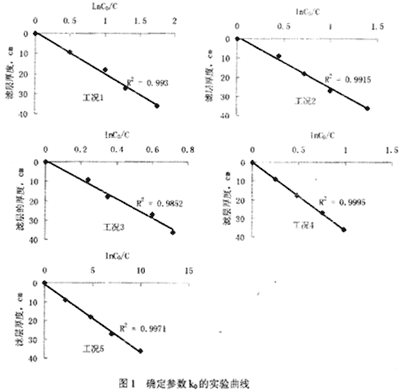
　　实验中测定了不同工况条件水头损失随时间的变化情况，相同粒径不同滤速时水头损失比较见图2，同一滤速不同粒径时水头损失比较见图3。

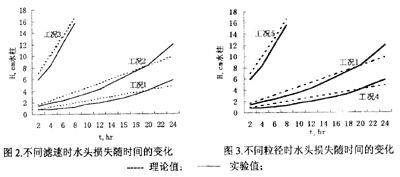
　　对于粒径为2.0-3.5mm的滤柱，当滤速为8m/h时，水头损失开始时增加很慢，12h后增长速度加快，过滤周期为24h；当滤速为10m/h时，水头损失的增长速度加快，过滤周期为16h；当滤速增加到15m/h时，水头损失增长速度很快，过滤周期缩短到8h；所以，建议滤速为8-10m/h。
　　对不同粒径的滤料进行实验时，滤速采用8m/h，实验结果见图2.8。当粒径很小(0.25－1.0mm)时，滤后水质很好，但水头损失增加很快，过滤周期为了8h。当粒径较大(3.5－5.0mm)时，水头损失增加缓慢，但出水水质较差。所以，采用的滤料粒径为2.0－3.5mm。
　　从图2和图3可以看出，理论值与实验结果吻合得较好。所产生的误差是因为在理论公式的计算中引用了几个经验参数，若对每一实际情况这些参数都能通过实验来测定，那么所得的计算结果会与实测值吻合得更好。

3 结论

　　改性滤料过滤除铁过程中水头损失增长规律不同于水的澄清过程，任一时刻水头损失的增加值可用公式计算。

参考文献：
　　[1]邓慧萍　改性滤料过滤除铁研究，同济大学学报　1995.8　pp427-431
　　[2]邓慧萍 严熙世　改性滤料过滤除铁的动力学模型　同济大学学报　2001.
　　[3]贝丽娜.A.M 等，地下水过滤除铁　给水杂志(俄文)　1983.22
　　[4]Wales S.M.　Resistance to filtration Trans.　American Inst.Chem.Eng.1964.5

作者简介：
　　邓慧萍：1964年生，同济大学环境科学与工程学院，副教授，博士，主要从事水处理理论与技术研究。