城市未来需水量预测方法研究
| 论文类型 | 技术与工程 | 发表日期 | 2001-10-01 |
| 来源 | 中国土木工程学会水工业分会给水委员会第八次年会 | ||
| 作者 | 高更超,崔玉川 | ||
| 摘要 | 高更超 崔玉川 (太原理工大学环工系 030024) 提要:本文对已有的城市需水量预测方法进行了归纳总结,简介了各自的特点和问题。对系统动力学的内涵进行了扼要介绍,在此基础上提出城市需水量预测的基本思路,建立了预测模型,研制出了城市未来需水量预测的计算机通用软件,并简介了使用要点。 ... | ||
高更超 崔玉川
(太原理工大学环工系 030024)
提要:本文对已有的城市需水量预测方法进行了归纳总结,简介了各自的特点和问题。对系统动力学的内涵进行了扼要介绍,在此基础上提出城市需水量预测的基本思路,建立了预测模型,研制出了城市未来需水量预测的计算机通用软件,并简介了使用要点。
一、现有需水量预测方法及问题
需水量预测是城市给水和节水发展规划的基础,其预测方法又是科学准确预测需水量的重要手段。国内外已有的预测方法较多,但其应用局限性和精确度尚存在一定问题。这些方法归纳起来大致可分为两大类,即时间序列法和结构分析法。
1、时间序列法
时间序列法是通过分析实际用水量与对应时间的历史数据,建立二者的对应关系,然后利用这种对应关系进行未来需水量的预测。主要有以下几种方法。
①、移动平均法
移动平均法以过去若干年用水数据的加权平均值来预测未来的需水量,如Vn为预测年需水量,过去m年用水量分别为Vn-1、Vn-2、……Vn-m,则其预测模型为:
Vn=(α1·Vn-1+α2·Vn-2+……+αm·Vn-m)/m
其中α1、α2、……αm为各年数据的加权系数。这种方法简便易行,适用于摆动情况,近期结果具有一定的准确性。但如用于远期预测,就会变成完全建立在预测数据上的预测,导致较大的偏差。
②、指数平滑法
该方法是对历史统计数据按时间序列适当加权,并大致加以平滑,根据变化规律来预测需水量。平滑可根据不同的要求分一次、二次以至多次进行。一般次数越多,精度越高,但计算量也越大。可用于非线性变化趋势。长期预测效果较差。主要模型有:
Vn+t=a+bt 或 Vn+t=a+bt+ct2
其中Vn+t为第t年预测需水量,a、b、c为平滑参数,t为预测期。
③、趋势预测法
先确定历史数据的变化趋势,如指数、对数或S型曲线,然后对其中未知参数进行估计,得出曲线方程,利用方程进行预测。该方法计算较简单,具有一定的精度。但结果不稳定。模型方程有:
Vt=atb+c
Vt=aet+c
Vt=ae-be-ct
其中a、b、c为未知参数,t为年份,Vt为对应年需水量。
④、马尔柯夫法
马尔柯夫法是利用上述任意一种方法得出趋势线,而后按数据波动的概率分布,得出未来波动的方向,对趋势值进行修正的一种预测方法。这种方法由于采用了马尔柯夫法进行“滤波”,可排除一定随机因素。但结果较不稳定。
⑤、灰色预测法
灰色预测法是利用灰色理论,建立城市需水灰色模型,利用该模型进行预测,灰色理论不要求对系统结构有较多了解即可进行预测,认为实际系统为不透明的“灰色箱体”。因此可根据其过去行为直接类推其未来行为,预测结果具有一定的精度。因实际理论及运算较为复杂,在此不再赘述。
2、结构分析法
与单纯考虑用水数据跟时间之间的联系不同,结构分析法具体分析城市需水量与各种相关因素之间的联系,试图揭示城市需水量的真正内含。其方法主要有:
①、回归分析法
该方法选取若干影响因素,对城市用水与这些因素之间的关系进行大致判断后,列出含未知参数的模型方程,代入实际数据,求出各参数。现有的回归分析法又可分为许多种,如经验回归法、线性回归法、指数回归法等。所选参数主要有人口、产值等。采用此种方法可进行中长期需水量预测,并具有一定的精度。但由于数学方法的局限,因素宜少不宜多。对应不同回归方法,存在不同的回归方程。如线性回归方程:
Vt=a0+a1x1+a2x2+……+ anxn
其中Vt为预测年需水量,a0~an为未知参数,x1~xn为相关因子。
②、弹性系数法
只用于工业用水需水量预测。工业用水弹性系数,在数值上等于工业用水增长率与工业产值增长率之比,即:
ε=α/β
ε--工业用水弹性系数
α--工业用水增长率
β--工业产值增长率
弹性系数法就是利用工业用水弹性系数基本不变这一规律来进行未来需水量的预测。在工业结构基本不变的情况下,使用该方法可得到比较符合实际的数值,用于中长期需水预测。
③、用水增长系数法
主要用于工业用水分行业预测。就某一行业而言,其用水增长系数可用下面方法求得:
r1=(V2-V1)/(Z2-Z1)
r2=(V3-V2)/(Z3-Z2)
… … …
rn=(Vn+1-Vn)/(Zn+1-Zn)
r=(r1+r2+……+rn)/n
其中,V、Z、r分别为产值、用水量及用水增长系数。
求出用水增长系数后,即可代入未来的规划产值,反推出未来的需水量。采用此法原理简单,计算量少。但由于工业结构的变动、节水措施的采用,会使得出的数值产生误差,有时会达到很高的程度。
结构分析法还有许多,在此就不再赘述。
这些预测方法的应用局限性,主要表现在两个方面:
1、预测对象不明,对需水量理解模糊。与未来水量有关的参数很多,现有方法多利用对历史取水数据进行分析、预测,而将预测结果称为需水量、用水量或取水量的都有,在概念上不够严密;
2、由于方法所限,仅能从数字趋势上寻求规律,无法深入系统内部,进行多因素、非线性关系的探讨。但是,由于城市用水系统发展的复杂性,此项工作的进行是十分必要的。因此已有的预测方法多采用简化的办法,如简化关系为线性、减少变量数目、采用灰箱模型等,使结果粗糙且应用范围较窄。而且,许多预测方法不能体现节水因素在系统发展中所起的重要作用,或者只能以笼统的定性预测来反映。
二、用系统动力学原理预测城市需水量
1、系统动力学概述
系统动力学(System Dynamics)是一门分析研究信息反馈系统的学科,也是一门认识和解决系统问题的综合性学科。它是系统科学和管理科学的一个分支,也是一门沟通自然科学和社会科学等领域的横向边缘学科,在我国只有十多年历史。
系统动力学的主要理论基础是信息反馈原理、决策理论及系统仿真技术。研究解决问题的方法是一种定性与定量相结合,系统分析、综合推理的方法。
系统动力学把所研究的对象看作是具有复杂反馈结构的、随时间变化的动态系统。它先将描述社会系统状态的各参量加以流体化,绘制出表示系统结构和动态特征的系统流图,然后把各变量之间的关系定量化,建立系统的结构方程式,以便运用专门的计算机语言进行仿真试验,从而预测系统的未来行为。
系统动力学解决问题的过程大致可分为五步:
①、系统分析。主要任务在于分析问题,剖析要因;
②、系统结构描述。主要是处理系统信息,分析系统的反馈机制;
③、建立系统的规范模型;
④、模型模拟与政策分析;
⑤、模型的检验与评估。
利用系统动力学方法,可以在缺乏基础数据、定量表达式难以建立的情况下,利用较少的变量来对系统发展的整体水平进行预测,并保证一定的精确度。因此,可以有效地克服目前城市需水量预测中的不确定性所带来的困难。在此即利用对城市用水系统动态分析所得结果,对未来城市在一定社会经济发展水平下的需水状况进行预测。
2、城市需水量预测的基本思路
城市用水系统的发展,表现在其各个子系统的具体指标变化上,这种变化的内因主要有以下四方面:
①、社会经济因素,如人口、经济结构、规模的变动;
②、用水效率因素,如工业用水复用率、万元产值取水量、中水回用、污水资源化等。
③、供水事业发展,如供水能力及漏失量控制等。
④、自然资源因素。如水资源总量、可开采量、降水量、径流量等的变化。
有关这些因素,不同城市有不同的特点。而且无论哪一方面,都与一定的政策、资金、管理、技术等水平息息相关。
如只利用第①方面因素研究未来城市用水系统的变化时,因为再不考虑城市其它因素,所得结果只具有一定理论意义,而对城市的实际发展作用不大。如在此基础上再对城市的用水效率因素予以考虑,此时所得的需水量,对城市远景规划和未来给、排水事业的发展,便具有实际指导意义,这便是本文的主要预测对象。
社会经济的发展,是城市取水需求的动力。对需水量进行研究,必须对未来预测水平年的社会经济发展状况有所了解,这些可从城市发展规划中得到明确的数据。
除此之外,还必须了解城市用水系统过去的发展状况。这就要求进行基础数据的收集工作,目的在于确定系统的内部反馈机制,建立各因素之间的联系,为确定城市未来系统的发展方向提供依据。这方面研究越透彻,预测就越接近实际。
从城市用水具体情况可知,实际取水需求量分生活需水及工业需水两部分。实际生活需水以人口及一定用水定额为基础,又受到中水回用、收费方式及水价状况等因素有关。而实际工业需水又与用水总需求量、工业用水复用率、城市污水回供工业用水量之间存在较为明确的数值关系。具体如下:
D实际=D生活+D工业
D生活=f(P用水,VUE大,V中水,W,......)
D工业+V回用=V工业总·(100-R工业)/100
其中
D实际──城市实际需水量(万m3/年),为考虑城市社会经济发展状况及用水效率因素后,某预测水平年的取水需求;
D生活──城市生活取水需求量(万m3/年),包括居民生活及城市公用事业用水、景观水等,即大生活需水量;
D工业──城市工业取水需求量(万m3/年),指城市工业发展所需新鲜水需求量。
P用水──城市预测年用水人口(万人);
VUE大──规划人均大生活定额(L/人·日);
V中水──中水使用量(万m3/年);
W──水价(元);
V回用──城市污水回供工业用水量(万m3/年);
V工业总──工业用水需求总量(万m3/年),包括工业生产中新鲜取水和各种形式的循环水、回用水、损耗水等。
R工业──工业用水重复利用率(%),指工业用水单元内部重复利用量所占比重。因城市污水回供量应作为外部供应水量,因此不能包括进来。
除了上述因素外,还有行政、资金、技术、管理等方面的作用,由于它们不是直接对需水量发生影响,而是通过对城市用水系统别的环节进行调整来间接作用于需水量,在此暂不列出,具体预测时,通过各种表函数的形式予以表达。
对城市未来需水量进行预测,便是以上式为基本关系式,考虑其它各种作用的影响,结合系统内部的反馈关系进行预测。为此,作生活需水及工业需水混合图1。
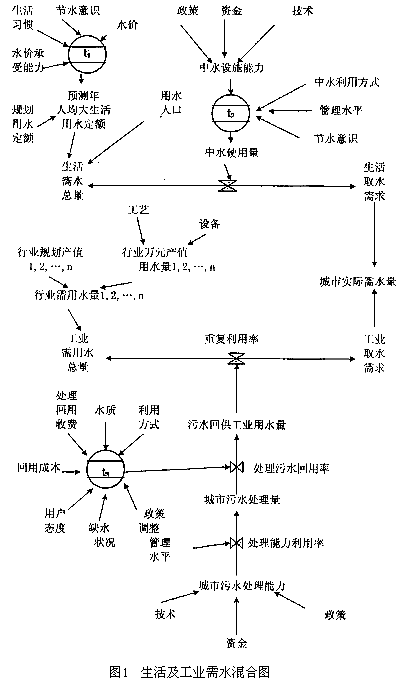
图1反映了上式的基本内容。其中有三个表函数t1、t2、t3, 做如下说明:
①、图中表函数t1反映了水价及生活需水之间的关系。其关系曲线形式如图2。对于不同城市,该曲线具体值会有所不同。这是由于不同城市人们的生活习惯、节水意识以及水价承受能力等因素所决定的。在确定该表函数时,应充分考虑上述因素。
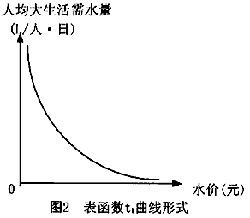
②、图中表函数t2反映了中水设施能力及中水实际用量之间的关系,其曲线形式如图3。在确定该表函数时,应考虑中水利用方式、管理水平以及人们节水意识等因素。
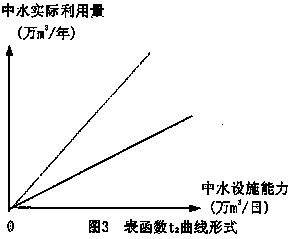
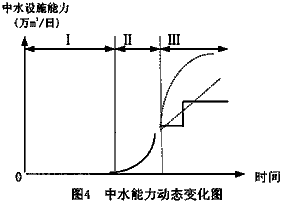
 ③、图中中水设施能力应随时间动态变化。该值的确定,应充分考虑到政策、资金、技术等方面的作用。随城市水资源的日趋紧张,中水设施能力应经过如图4中的阶段性变化。第I阶段为水资源充足时,无中水设施投建;当水资源紧张初期,在政策调整作用下,中水设施建设力度逐渐加大,为第II阶段;此后,由于资金、技术等因素的限制,中水设施建设可能呈现线性变化、阶段跳跃变化或渐近变化等形式,为第III阶段。
③、图中中水设施能力应随时间动态变化。该值的确定,应充分考虑到政策、资金、技术等方面的作用。随城市水资源的日趋紧张,中水设施能力应经过如图4中的阶段性变化。第I阶段为水资源充足时,无中水设施投建;当水资源紧张初期,在政策调整作用下,中水设施建设力度逐渐加大,为第II阶段;此后,由于资金、技术等因素的限制,中水设施建设可能呈现线性变化、阶段跳跃变化或渐近变化等形式,为第III阶段。
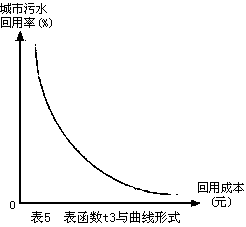
④、表函数t3反映了经处理城市污水的工业回用比率与回用成本之间的关系。一般而言,随回用成本的增加,回用比率有逐渐降低的趋势。此关系的确定,主要需考虑处理水质、利用方式、回用水收费标准、用户态度、政策调整等作用。其曲线形式如图5。
⑤、城市污水处理能力利用率,主要按照城市现阶段管理水平及其发展趋势确定。
⑥、城市污水处理能力由于城市的决策、资金、技术等各反面的作用不同而具有不同变化形式。
依据图1,就可以建立城市未来需水预测模型。通过上述分析可知,建立模型的主要支撑工具便是图中各变量及其关系,通过表函数,可以考虑到许多以前无法考虑的因素。
3、城市需水量预测模型及相关因子
依据上述思路及系统反馈机制,城市需水预测的分步骤模型如下:
①、D实际=D生活+D工业
②、D生活=D生活总-V中水
D工业=V工业总·(100-R工业)/100-V回用
③、D生活总=P用水·Min[t1(W),VUE大]·0.365
V中水=t2(C中水)
t1=f1(节水意识,生活习惯,物价承受能力......)
t2=f2(利用方式,管理水平,节水意识,……)
C中水=f3(政策,投资,技术,……)
④、V工业总= = /1000
V回用=V处理·R回用/100
V处理=365·C处理·R处理/100
R回用=t3(F回用)
R处理=f4(管理水平,……)
t3=f5(回用收费,处理水质,用户态度,……)
C处理=f6(政策,技术,资金,……)
其中
D生活总--预测年城市生活需水总量(万m3);
C中水--预测年城市中水设施能力(万m3/日);
V行业i--预测年城市第i工业行业用水总量(万m3);
VUPi--预测年第i工业行业万元产值用水量(m3/万元);
GPi--预测年第i工业行业总产值(万元);
V处理--预测年城市污水处理量(万m3);
C处理--预测年城市污水处理能力(万m3/日);
R回用--预测年城市污水回用工业占城市污水处理总量份额(%);
F回用--预测年城市污水回用成本(元);
R处理--预测年城市污水处理量占排放总量份额(%);
t1~t3--表函数;
f1~f6--表示相关关系;
其余同前所述。
在实际预测时,考虑目前普遍水资源短缺的影响,按不同缺水程度,城市实际需水量需用不同系数予以调整。本模型中,对于年供水量已达可开采量60%的城市予以调整。具体而言,年供水量达可开采量60%~80%者,实际生活需水量加上5%,实际工业需水量加上6%;年供水量达可开采量80%~100%者,实际生活需水量加上6%,实际工业需水量加上8%;年供水量已超过可开采量者,实际生活需水量加上8%,实际工业需水量加上10%。
则最终城市需水预测模型如下:
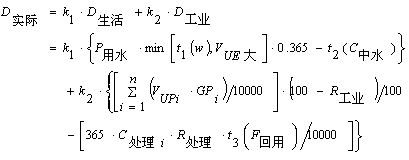
式中,k1、k2为视不同缺水状况下的不同系数。k1可为1.05、1.06、1.08;k2可为1.06、1.08、1.10。
从上述预测模型的建立可以看出,该模型考虑到了许多以前无法考虑或由于其他原因而没有考虑到的因素。该模型主要考虑因素如下:
⑴、节水管理水平的作用;
⑵、水价的影响;
⑶、定额的作用;
⑷、人们的节水意识;
⑸、政策调整作用;
⑹、资金的投入;
⑺、中水设施建设;
⑻、用水人口的变化;
⑼、行业用水效率;
⑽、不同工业结构的影响;
⑾、行业产值的变动;
⑿、工艺节水因素;
⒀、污水回用成本;
⒁、城市缺水状况;
⒂、污水回用方式、收费、及用户的态度等;
⒃、城市污水处理能力;
⒄、工业用水重复利用率;
等等。
4、需水量预测软件及使用
城市用水系统是一复杂社会系统,其中的信息流,种类繁多,生命期短,仅靠人工进行收集、整理、加工、应用,费时费力却事倍功半,经常导致信息流偏差或障碍。为解决此问题,需利用电脑强大的数据处理功能,代替人工进行枯燥的数字处理工作。由于需水量预测计算量较大,我们编制了计算机通用软件,以代替人工进行工作。本软件的目的是将所得预测模型,以可运行计算机软件的形式表达出来,使这项工作得以更为快速、准确的进行。
软件利用面向对象方法进行开发研制,采用事件驱动机制,不是顺序执行结构,而是采用交互响应方式,按用户指令进行工作。
本软件所需数据主要有:标准类、城市固有基础数据类、城市历年基础数据类、城市预测水平年社会经济发展数据类、分析处理所得数据类。这些数据,除部分中间结果外,均按一定方式在计算机中予以存储,以备修改或查询。
本软件可以完成城市需水量的预测工作。F2为城市基础数据录入; F7为城市需水量预测;F8为决策分析。
通过系统专门的“数据录入”功能,可进行需水预测所需数据录入。如果在预测时数据不全,系统所得数据可能会与实际情况大相径庭。所以请务必将所需数据全部输入。
进入“需水预测”菜单,可选择“需求预测”及“决策分析”两种功能。需水预测时,系统将提示输入预测城市、现状年、预测年以及是否在预测前对现状年数据进行浏览(在此无法对实际数据进行修改),预测期不能大于50年。而后要求对预测所需预测期数据进行输入。为简化数据录入工作,系统提供了三种规律以供选择:①、线性变化;②、指数变化;③、渐进变化。如果数据变化不完全符合某一规律,可以通过系统提供的数据微调功能来录入。
系统还可进行“决策分析”来研究不同决策对未来需水量所起的作用。此时,如不选择“取消”(Esc键),系统将提示用户目前的需水预测结果,并要求改变决策数据,用户确认后,再次将新的预测结果告知用户,不断循环,直到用户取消为止。
参考文献:
1. 王其藩,《系统动力学(修订版)》,清华大学出版社,1994.10
2. 胡玉奎,《系统动力学》,中国科技咨询服务中心,1989.6
3. 《中国城市建设年鉴(1986-1987)》,中国建筑工业出版社,1989.3
4. 《城市供水统计年鉴(1993)》,中国城镇供水协会,1994
5. 王占鄂、李东祥,《城市用水管理》,济南出版社,1992.5
6. 常明旺、侯继文,《工业用水管理技术》,山西科学教育出版社,1991.4
7. 侯文超,《经济预测-理论、方法及应用》,商务印书馆,1993
8. 丁宏达,“用回归-马尔柯夫链法预测供水量”,《中国给水排水》,1990,vol.6,NO.6
9. 董辅祥,“城镇与工业企业水资源需求预测方法的识别及应用”,《给水排水》,1984.4
10. 洪觉民,“关于城市用水量的预测”,《给水排水》,1985.4
11. 崔玉川,“工业节水经济效益分析评价”,92‘全国工业水委年会论文,1992.12
12. 李铭,“水资源规划中的灰色系统理论方法”,1993.3
13. 王大哲,“预测城市工业取水量的一种新尝试”,《给水排水》,1996.1
14. William E. Martin & Susan Kulakowski, Water Price as a Policy Variable in Managing Urban Water Use: Tucson, Arizona, Water Resource Research, Vol.27,No.2,1991.Feb
15. 《Borland C++实用类,算法及类库编程》,科学出版社,1994.5
16. Herbert Schildt, C:The Complete Reference, Second Edition, Osborne McGraw-Hill,1990
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 [email protected] ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








