石灰石脱硫反应活性的研究
| 论文类型 | 基础研究 | 发表日期 | 2001-07-01 |
| 来源 | 贺李圭白院士七十寿辰学术论文集 | ||
| 作者 | 李星,杨艳玲 | ||
| 关键词 | 石灰石 脱硫 反应活性 动力学模型。 | ||
| 摘要 | 脱硫剂石灰石的反应活性对流化床燃煤锅炉的脱硫效果影响很大。目前,国内外主要采用动力学方法,通过测定固态CaO的硫酸盐化程度来推断石灰石的反应活性。但这在石灰石中含有许多其它杂质成分时是不够全面的,因为这些杂质成分对石灰石的脱硫反应活性影响很大,不能忽视。 本文通过测定流化床入口和出口的SO2浓度变化来判断加入床中的石灰石样品的反应活性。由于凡是能引起SO2浓度变化的物质都与石灰石的反应活性有关,从而克服了原有方法仅考虑CaO重量变化的片面性。 本文也采用了动力学方法建立了石灰石反应动力学模型, | ||
李 星 杨艳玲 李 磊
(哈尔滨建筑大学) (哈尔滨理工大学)
摘 要:脱硫剂石灰石的反应活性对流化床燃煤锅炉的脱硫效果影响很大。目前,国内外主要采用动力学方法,通过测定固态CaO的硫酸盐化程度来推断石灰石的反应活性。但这在石灰石中含有许多其它杂质成分时是不够全面的,因为这些杂质成分对石灰石的脱硫反应活性影响很大,不能忽视。
本文通过测定流化床入口和出口的SO2浓度变化来判断加入床中的石灰石样品的反应活性。由于凡是能引起SO2浓度变化的物质都与石灰石的反应活性有关,从而克服了原有方法仅考虑CaO重量变化的片面性。
本文也采用了动力学方法建立了石灰石反应动力学模型,并利用线性化方法对其反应速率常数K进行了线性估计,建立了石灰石化学成分与活性关系的数学模型。
关键词:石灰石,脱硫,反应活性,动力学模型。
Study of Desulphurization Reaction Activity of Limestone
Li Xing★, Yang Yan-Ling★ Li Lei※
(★Harbin University of Architectural and Civil Engineering)
(※Harbin University of Science and Engineering)
ABSTRACT:The reaction activity of desulphurizer limestone has a great effect on the desulphurization result of fluidized bed coal-burning boilers. Now the method of dynamics is used in normal applications by measuring the sulphation degree of the solid calcium oxide to infer the reaction activity of limestone. But it is not enough on condition that there is much type of impurity composition within the limestone, which has considerable influence on the desulphurization reaction activity of limestone.
The change of sulfur dioxide concentration of inlet and outlet of the fluidized bed is measured to determine the reaction activity of limestone samples in the bed in this article. Because the material which will lead to the change of sulfur dioxide concentration has a relation to the reaction activity of limestone, therefore, this method overcomes the one—sidedness of the method above, which only considers the weight change of calcium oxide. The method of dynamics is applied to establish the dynamic model of limestone reaction, and linearization method is employed to make linear estimates of reaction rate constant K so that the mathematical model between chemical composition and activity of limestone is built up.
Key words: limestone; desulphurization; reaction activity; dynamic model.
向流化床锅炉的燃烧区加入石灰石,首先发生的是石灰石的高温分解,分解产物为CaO。CaO颗粒在O2过量条件下,与SO2发生硫化反应,生成CaSO4,即:
CaO+SO2+1/2O2=CaSO4+486kj/mol (1)
石灰石的反应活性对反应式(1)的反应程度影响很大。因此,国内外有关研究人员对此进行了大量的研究工作[1~3],实验主要采用热重分析(TGA)法,测定的对象一般为CaO的硫酸盐化程度,并以此为基础研究石灰石的脱硫反应活性。由于该方法的测定对象为固态,故简称之为“固测法”。但是,用固测法研究石灰石的活性,有时存在较大的偏差。TGA法的吸硫曲线的增重趋势总是被认为是按反应式(1)中CaO吸收SO2和O2生成CaSO4所造成。而实际上,石灰石中除了主要成分CaCO3外,还含有许多其它杂质成分。一些杂质成分经高温分解后产生的一些碱性氧化物同样也能与SO2和O2反应生成硫酸盐。另外一些杂质成分还会生成一些复杂的复合物,从而间接地影响反应(1)的进行,这些情况都会给热重分析带来不可避免的误差,而也影响了石灰石活性数据的准确性。
本文的研究方法是将测定对象由TGA法的固测改为对SO2的气测。在流化床脱硫模拟试验台上,通过监测SO2浓度的变化研究石灰石的反应活性。在特定的工况条件下,SO2在通过吸硫剂石灰石时浓度变化可以认为是由于石灰石固有特性所引起的,它体现了石灰石总体吸硫效果,这样就避免了由于仅仅考虑CaO的转化而忽略了其它杂质成分影响带来的活性数值的偏差。本文将以流化床典型运行温度850℃下的反应速度常数作为石灰石脱硫活性的指标。
1.材料与方法
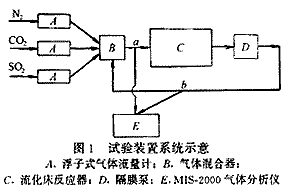
试验采用流化床反应器模拟法。全部试验在石灰石脱硫反应活性试验台上进行,图1为试验流程简图。N2、CO2和SO2经流量计A进入气体混合器B,在a点用MIS-2000烟道气体分析仪E对混合气体的SO2初始浓度进行测定。当SO2流经a点进入反应器C时,脱硫反应开始进行。每间隔10min在b点用气体分析仪E对SO2的浓度进行一次测定,直到SO2的浓度不再改变时为止,此时,试验结束。为了模拟流化床的实际工况,石灰石的热解与脱硫在反应器中同时进行(这与TGA法不同),反应温度设置为流化床典型运行温度850℃。
2.动力学模型的建立
反应式(1)的速度公式为:
r=-dCA/dt=KCXACYB (2)
式中,r为脱硫反应速度;t为反应时间;CA为t时刻的SO2浓度;CB为t时刻的O2浓度;x和y分别为SO2和O2的表观反应级数。Lee[4]等人研究石灰石在流化床中与SO2的反应物性时指出:因为反应是在氧过量的条件下进行的,所以固硫化反应对于 SO2是一级反应,而对于O2是零级反应。于是,根据这一结论可将(2)式简化为:
r=-dCA/dt=KCA (3)
采用积分法,将(3)式移项积分:
![]() (4)
(4)
当t=0时,SO2的浓度为C0,当t=t时,SO2的浓度为C0。对(4)式积分后即得到:
C=C0exp(-Kt) (5)
3.石灰石脱硫反应活性的求取
将(5)式两边取对数,得
lnC=lnC0-Kt (6)
(6)式可转换为:
Y=b+aX (7)
由式(7)可见,变量X与Y之间成线性关系。因此,可以线性回归确定参数a、b及线性相关系数R。使用ppp-60程序上机运算,得到的结果列于表1。
由表1可见,线性相关系数在0.95以上,查t分布的ta值表,t0.0005=-5.405。表1中所有的t检验值均小于-5.405,说明有1-α=1-0.0005=99.95%的把握拒绝μ=0的零假设[5]。
表1 运算结果
序号
回归式![]() =b+ax
=b+ax
反应速度常数K
(850℃)
相关系数R
t检验值
1
![]() =8.000-1.794×10-2 x
=8.000-1.794×10-2 x
1.794× 10-2
0.9712
-9.990
2
![]() =7.886-1.374× 10-2 x
=7.886-1.374× 10-2 x
1.374× 10-2
0.9506
-7.505
3
![]() =7.968-8.843× 10-2 x
=7.968-8.843× 10-2 x
8.843× 10-2
0.9960
-27.42
4
![]() =7.807-1.794× 10-2 x
=7.807-1.794× 10-2 x
1.794× 10-2
0.9764
-11.08
5
![]() =7.912-1.409× 10-2 x
=7.912-1.409× 10-2 x
1.409× 10-2
0.9936
-21.63
6
![]() =7.884-1.708× 10-2 x
=7.884-1.708× 10-2 x
1.708× 10-2
0.9885
-16.03
7
![]() =7.849-7.160× 10-2 x
=7.849-7.160× 10-2 x
7.160× 10-2
0.9644
-8.935
8
![]() =7.792-1.795× 10-2 x
=7.792-1.795× 10-2 x
1.795× 10-2
0.9794
-11.89
9
![]() =7.879-1.519× 10-2 x
=7.879-1.519× 10-2 x
1.519× 10-2
0.9891
-16.48
10
![]() =7.778-1.665× 10-2 x
=7.778-1.665× 10-2 x
1.665× 10-2
0.9837
-13.38
11
![]() =7.752-1.808× 10-2 x
=7.752-1.808× 10-2 x
1.808× 10-2
0.9864
-14.70
12
![]() =7.857-1.022×10-2 x
=7.857-1.022×10-2 x
1.022× 10-2
0.9708
-9.905
13
![]() =7.857-1.431× 10-2 x
=7.857-1.431× 10-2 x
1.431× 10-2
0.9831
-13.15
表1 运算结果 续表
序号
回归式![]() =b+ax
=b+ax
反应速度常数K(850℃)
相关系数R
t检验值
14
![]() =7.794-2.001× 10-2 x
=7.794-2.001× 10-2 x
2.001× 10-2
0.9816
-15.43
15
![]() =7.777-2.048× 10-2 x
=7.777-2.048× 10-2 x
2.048× 10-2
0.9833
-13.23
16
![]() =7.783-1.677× 10-2 x
=7.783-1.677× 10-2 x
1.677× 10-2
0.9760
-10.96
17
![]() =7.868-1.510× 10-2 x
=7.868-1.510× 10-2 x
1.510× 10-2
0.9788
-11.71
18
![]() =7.788-1.788× 10-2 x
=7.788-1.788× 10-2 x
1.788× 10-2
0.9714
-10.02
19
![]() =7.900-1.811× 10-2 x
=7.900-1.811× 10-2 x
1.811× 10-2
0.9761
-11.01
20
![]() =7.844-1.749× 10-2 x
=7.844-1.749× 10-2 x
1.749× 10-2
0.9790
-11.76
4.石灰石化学成分与活性关系
以反应活性k作为因变量,化学成分为自变量,建立多元线性回归方程。为了保证方程的稳定性,采用逐步回归分析法[6]将一些次要成分给予剔除,最后得到回归方程为:
![]() (8)
(8)
复相关系数R=0.9722,残差平方和Q=1.275×10-5,剩余标准差S=9.544×10-4,F检验值F=80.48。可见,方程(8)的回归拟合优度较高。
5.结论
1.采用气测法获得的石灰石脱硫反应速率常数K,可以全面地反映石灰石脱硫能力,避免了固测法由于石灰石杂质造成的误差。
2.由式(8)可知,石灰石的反应活性与杂质成分有一定的数量关系。值得注意的是[MgCO3]在方程中对k具有负效应,这似乎有些不可思议,这是因为[MgCO3]的分解产物MgO的反应活性与压力有关。MgO由于在常压下与SO2的反应非常之慢,可视为惰性,所以MgCO3一般在增压流化床内才具有良好的脱硫作用。
3.利用式(8)可对石灰石的反应活性进预测,例如:当[CaO]=50%,[MgCO3]=6.2%,[SiO2]=3.42%,[Fe2O3]=0.08%,[Al2O3]=0.2%时,可求得K=1.763×10-2。
参考文献
1. Dennis J.S. and Hayhurst A.N.,“A Simplified Analytical Model for the Rate of Reaction of SO2 with Limestone Particles”, Chemical Engineering Science, 1986, 41:25~36.
2. James R.H. et al. “Testing of Limestone Sample from the TVA Region as Sulfur Dioxide Sorbent in AFBC”, Institute for Miningang Minerals and Research Kentucky Center for Energy, Research Laboratory and Tennessee, Valley Authority, 1984.
3. 国家环保局,“大气污染防治技术研究”。北京科学出版社,1993,370~373.
4. Lee D.C., et al. “A Single Particle Size Model for Sulfur Retention in Fluidized Bed Coal Combustors”. AICHEJ, 1981, 27: 472~480.
5. 中国科学院数学研究所,“回归分析方法”。北京:科学出版社,1974,29~32.
6. 邢英等,“经济统计分析及预测”。北京:清华大学出版社1982,109~119.
注:原刊于《中国环境科学》,1998年,第1期。
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 [email protected] ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








