非稳态工况对曝气池处理效果的影响

闫来洪，赵朝成
(石油大学化学化工学院，山东东营　257062)

　　摘　要：采用数值法对曝气池非稳态工况下的处理效果进行了计算分析，结果显示，考虑非稳态工况所确定的曝气池容积，能较好地适应进水冲击负荷，可供采用传统设计方法时参考。
　　关键词：数值法；曝气池；非稳态工况
　　中图分类号：TU992.02
　　文献标识码：C
　　文章编号：1000-4602(2001)06-0036-04

　　完全混合式活性污泥法是目前采用较多的生物化学处理方法。其特点是混合液在池内充分混合循环流动，因而污水与回流污泥进入曝气池后立即与池内原有混合液充分混合，进行吸附和代谢活动，并顶替等量的混合液至二次沉淀池。目前在工程设计中大都采用污泥负荷率和污泥龄来计算曝气池的总容积，然后根据运行操作的需要将曝气池平均分成几个单池［1］，其计算的理论基础是基于池内污染物浓度和微生物浓度对时间的变化率为零的假定，即曝气池完全是处在稳态条件下运行。鉴于非稳态情况下设计计算较为复杂，过去又受计算工具的限制，以前均不考虑非稳态情况的影响。然而，在工程实践中曝气池进水污染物浓度有时波动较大，尤其是在规模较小的工业企业和小城镇的污水处理系统中，为节省投资，大都没有设计完备的水质调节池，进水水质波动的情况就更普遍，因此非稳态工况对出水水质的影响比较明显。如果在设计阶段对非稳态工况的影响作适当考虑，将可大大改善非稳态工况的冲击影响。目前，由于计算机的普及与应用，复杂的非稳态工况下的设计计算已不成问题。正是从以上原因出发，采用数值方法对非稳态工况下完全混合曝气池容积进行了分析计算，为完善曝气池的设计方法进行了初步探索。

1　曝气池内物料平衡方程

　　根据池内污染物的质量平衡关系，在(t,t+Δt)内曝气池中污染物的物料平衡存在如下关系：
　　　　　　改变量=进入量-排出量-分解转化量
　　假设①有机物被微生物分解、转化产生而消失的速率(单位时间的百分比)与微生物浓度成正比，比例系数为k1［L/(mg·h)］；②微生物的内源呼吸衰亡率(单位时间的百分比)是常数D=10-5/h；③池内污染物和微生物在任何时候都是均匀混合的，于是可以用C(t)和b(t)分别记污染物和微生物的浓度，即它们只是时间t的函数，而与位置无关。并且由此认为排出的废水中污染物和微生物的浓度与池内相同；④废水进入曝气池的流量Q(m³/h)不变，池内废水量不变。忽略池内废水的蒸发等因素，可以认为排出的水量与Q相同，并且近似地设池内水量等于池的容积V，即水是满池的。根据以上假设有：
　　V［C(t+Δt)-C(t)］=QC₀Δt-QC(t)Δt-k₁b(t)C(t)VΔt
　　由此可得微分方程：
　　dC／dt=QV(C₀-C)-k₁bC(1)
　　类似地，根据池内微生物的平衡关系,在(t,t+Δt)内曝气池中微生物的浓度变化存在以下关系：
　　改变量=增加量-衰亡量-排出量
　　在前面所述假设的基础上，再假设：⑤微生物依靠污染物分解、转化产生的能量而增殖的速率(以单位时间的百分比计)与污染物的浓度成正比，亦即产率系数k2；⑥微生物的自身氧化率(单位时间的百分比)是常数D。有：
　　V［b(t+Δt)-b(t)］=k₂C(t)b(t)VΔt-Db(t)VΔt-Qb(t)Δt
　　可得方程：
　　db／dt=(k₂C-D-Q／V)b　　　　　　　　　　　　　(2)
　　式(1)、(2)给出了池内污染物浓度和微生物浓度的变化规律。

2　曝气池容积计算分析

　　根据某石油化工厂实际排水的情况按式(1)、(2)计算分析所需曝气池处理池的容积。该厂排出废水中的污染物浓度在0.001～0.01 mg/L之间，采用生物处理法将其浓度降至排放标准规定的0.000 5 mg/L以下。已知废水以10 ｍ3/h的流量进入处理池，进入曝气池的废水中污染物浓度为C0，则10^-3=C₀₁≤C₀≤C₀₂=10^-2(g/m³)。C₀可以保持某个定值，也可随时发生变化，最坏的情况(对于生物处理而言)是C0由C01突然增加到C0²。根据试验测得的k1=0.1m³/(g·h),k₂=1.26m³/(g·h)，D=10^-5/h。处理目标须达到长期稳定排放时不应超过规定的排放标准C^*=5×10^-4 mg/L。
　　式(1)、(2)联立非线性方程组难以求出解析解，但可分别讨论它的稳态和非稳态过程。
　　方程(1)、(2)有两个平衡点

　　P1：C=（D+Q/V）／k₂，b=Q(C0-C)／Vk₁C　　　　(3)
　　P₂：C=C₀,b=0
　　可以验证在C＜C0的条件下P1稳定，P2不稳定。由式(3)可知，为了b＞0必须有C＜C₀，而这个条件等价于要求：
　　V＞Q／k₂C₀-D　　　　　　　　　　　　(4)
　　显然C0越小V应越大，用C0＝C01和Q、k₂、D代入式(4)可得V＞8 000 m3，而要使稳定情况下的C不超过规定标准C≤C*，则应使：
　　V＞Q／k₂C^*-D≈1.6×10⁴m³(5)
　　考察最不利的情况：当C₀=C₀₁=10^-3(g/m³)时池内已处于稳态，t=0时C₀突然增至C₀₂，在方程(1)、(2)中令C₀＝C₀₂，以式(3)算出的稳定平衡点(其中C₀=C₀₁)为初值C(0)、b(0)，采用数值法解微分方程组的龙格—库塔方法分别计算V=1.6×10⁴m³时和V=3×10⁴m³的C(t)，所得结果如图1所示。

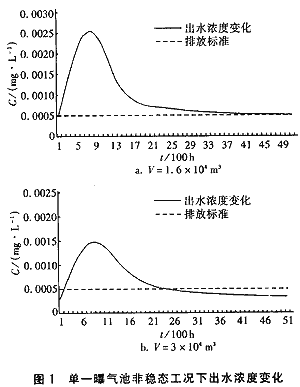
　　经以上分析计算可见，首先，处理池的容积V必须满足式(4)，否则平衡点P₁不稳定，而P₂稳定，这可以解释为，当(D+QV)＞k₂C0，即微生物衰亡和排除的速率大于增殖率时，微生物浓度不能增长，处理方法失败。其次，由式(3)可知池内污染物的稳定浓度C与入池的浓度C₀无关，所以不论C₀是给定区间［C₀₁，C₀₂］中的哪一个值，为了使处理后的稳定浓度不超过C*，池的容积最小应为1.6×10⁴m³［见式(5)］。但是，非稳态过程的计算表明，当污染物的入池浓度由C₀₁突增至C₀₂时，用这个容积的曝气池将有约1 300 h的出水污染物浓度超过排放标准C^*的2倍，且最高可达C^*的5倍(图1a所示)。即使将池容增至3×10⁴m³(图1b)，也有近900 h的出水污染物浓度超过排放标准C^*的2倍。由此可见，采用单一池子在满足必须的池容时，不能较好地适应非稳态情况的冲击影响。
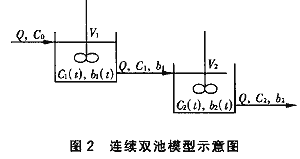
　　考虑采用两个池子串连的情况，相应的假设条件不变，池1的排出是池2的流入，各个量的符号如图2所示。
　　对于池1，其方程形式同式(1)、(2)。
　　对于池2，污染物浓度C₂(t)的方程只须注意到入池浓度是C₁即可写出：
　　dC₂／dt=Q／V₂(C₁-C₂)-k₁b₂C₂　　　　　　(6)
　　而微生物浓度b2(t)的方程中则需加上由池1到池2的微生物的流入量，即：
　　db₂／dt=(k₂C₂-D-QV₂)b₂+（Q／V₂）b₁　　　　　　(7)

　　关于稳态情况，池1的平衡点及稳定性与单池情形相同。
　　池2的平衡点(C2,b2)满足：

　　　　　　　　　b₂=Q(C₁-C₂)／V₂k₁C₂　　　　　　　　　　　　　　　　　　(8)
　　　　　　　　　k₂C₂2-(k₂C₁+k₁b₁+D+Q／V₂)C₂+C₁(D+Q／V₂)=0　　　　　　(9)

　　式(9)有两个根，因为要保证C1＞C2(b2＞0)和(C2,b2)稳定，只取：

　　　　　C₂=1／2k₂{(k₂C₁+k₁b₁+D+Q／V₂)-[(k₂C₁+k₁b₁+D+Q／V₂)²-4k₂C₁(D+Q／V₂)]^1/2}　　　　　(10)

　　要使稳定状态下的C2≤C*，由式(9)可得V2必须满足：

　　　　　　　V₂≥Q(C₁-C^*)／(C₁-C^*)(k₂C^*-D)+k₁b₁C^*　　　　　　　(11)

　　由式(3)、(11)可知，C₀越小时b₁越小，V₂应越大，所以仍令C₀=C₀₁,在V1≥8×10³m³的几个取值下计算C₁、b₁和V₂(C₂≤C^*)，结果如表1所示。

表1　C₀=10^-3，C₂≤C^*下的稳态结果 V₁(10³m³) C₁(10^-3g·m^-3) b₁(10³) V₂(10³m³) 8 1.0 0.02 16.03 10 0.8 2.50 9.63 12 0.67 4.14 5.39 14 0.57 5.31 2.37 16 0.50 6.18 0.096

　　从表1可以看出，在稳态情况下较大的V1和较小的V₂组合是较理想的方案。
　　关于非稳态过程，仍考察C₀由C₀₁突增至C₀₂的最不利情况。取V1＝14 000m³,V2＝7 000 m3,用数值龙格—库塔法计算C₂(t)，结果如图3a所示，虽仍有约1 100 h超过C^*，但基本上不超过2C^*了。
　　经计算，欲使非稳态过程中始终保持C₂(t)≤C*，第二个曝气池的容积为V2＝10 000m³，计算结果如图3b所示。

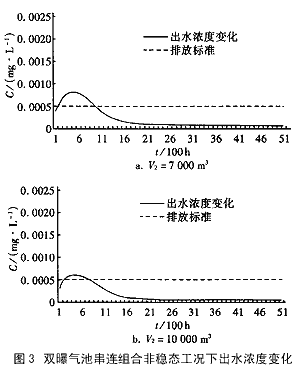
　　采用双池比使用单池有明显的进步。用单池V=3×10⁴m³的出水浓度曲线与双池V1＝1.4×10⁴m³、V2=7×10³ m³时的出水浓度曲线相比，双池的总容积减少了近1/3，而处理效果却比单池好得多。即便使全部出水合格的组合双池V1＝1.4×10⁴m³，V2=7×10³m³形式，容积也比单池容积小很多，从经济上考虑，采用双池是首选方案。

3　结论

　　考虑到曝气池运行最不利的非稳态工况，运用数值法解微分方程组，求得的曝气池容积能更好地适应非稳态工况的冲击影响，满足出水污染物在任何时候达标排放的要求，设计出的曝气池组合更符合工程实际，甚至无需在曝气池前设置调节池，也能满足处理要求。将非稳态工况作为曝气池设计时的一个考虑因素，在进行小型污水处理流程设计、又不便设置污水调节装置时，且存在非稳态冲击负荷的情况下，可以采用以上思路进行传统活性污泥曝气池的容积设计。

参考文献：

　　［1］崔玉川，马志毅.废水处理工艺设计计算［M］.北京：水利电力出版社，1994.
　　［2］李学春，等.计算方法［M］.山东：石油大学出版社，1998.
　　［3］姜启源.数学模型［M］.北京：高等教育出版社，1993.
　　［4］Larry D Benefield，Clifford W Randall.Biological Process Design for Wastewater Treatment［M］.刑建，等译.北京：中国建筑工业出版社，1984.
　　［5］哈尔滨建筑工程学院，排水工程(下)［M］.北京：中国建筑工业出版社，1987.

---

　　电　话：(0546)8393524(O)8396173(H)
　　E-mail:[email protected]
　　收稿日期：2000-09-15