给水管网水力模拟计算算法的优化

魏宝成，袁一星，郭爽
（哈尔滨工业大学给水排水系统研究室）

　　摘要：本文介绍了给水管网水力模拟计算的算法，以及提高水力模拟计算软件计算速度的方法。
　　关键词：给水管网；水力模拟

Optimization of Simulation Algorithm in Water Supply Network
Wei baocheng, Yun yixing, Guo Shuang
(Workgroup of Water & Wastewater System, Harbin Institute of Technology)

　　Abstract: This paper describes the algorithm of water supply net1work simulation and the method to accelerate the calculation of water supply network simulation software.
　　Key words: water supply network; hydraulic simulation

　　在供水综合管理信息系统中，供水管网的水力模拟计算软件处在一个非常关键的位置，是整个系统的“核心”所在。
　　由于城市规模的扩大，供水管网的规模也越来越大，管网计算的运算量也越来越大，以往的计算程序在计算几十个节点的管网时还能胜任，而当进行几百、几千、甚至上万个节点的大规模管网时，其速度就变得无法令人忍受。另外在现代数学中，有很多优化理论，单从理论本身出发是可以应用于供水管网的优化计算、实时调度方面，但由于管网信息量大，管网模拟计算软件的速度较慢，进行一次计算，往往需要几个小时、几天，这样的计算结果对指导实践是没有实际意义的，因此提高供水管网水力计算的速度是一个重要的课题。

1、理论基础

　　对给水管网进行水力模拟总是联立求解连续性方程、能量方程和压降方程。其中解节点方程是联立压降方程和连续性方程，是现在多数水力计算程序采用的算法。
　　所谓连续性方程，就是对任一节点来说，流向该节点的流量必须等于从该节点流出的流量。

　　　　　Q_i+Σq_ij=0

将管段的压降方程代入连续性方程，则任意一个节点的连续性方程可写成：

　　

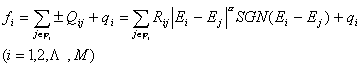
　　式中指数α=0.54，Ｍ为节点数(不包括已知节点)，q_i为节点流量(m³/s)。式中l表示管段号，i,j表示管段l的上下游节点标号，所谓上下游是这样规定的，管段l的计算流向（参考流向）是从节点i流向节点j的。
　　这是一个非线形方程组，不能直接得到其解析解。解非线形方程组比较困难，方法有多种，比较常用的是牛顿-拉斐森方法。
记E为以E_i为分量的向量，f为以f_i分量的向量，在E的领域内可进行泰勒级数展开：

　　

　　偏导数构成的矩阵是雅可比(Jacobian)矩阵J

　　

　　可以得到：

　　

　　

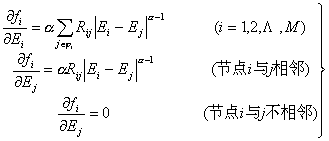
　　忽略高阶项，并置F(E+δE)=0,将可得到一个关于修正项δE的线性方程组。即

　　　　J·δE=-F

　　其中δE可使每个函数都同时接近于零。
　　整个这一过程就是非线形方程组的“线形化”过程，可变化成解一个线性方程组，并将求出的修正项加到解向量中：

　　　　E_new=E_old+δE

　　这个过程不断迭代，直到收敛为止。

2算法的优化

2.1系统选用了高效的算法
　　1.牛顿法虽然已经不能算是一个新算法，但它在收敛速度上有着无可比拟的优势，并且后面我们提到，可以对它适当改造，来克服它自身的缺点。
　　2.改进平方根法是解线性方程组直接解法中速度最快的一种，由于其很好的利用了连续性方程雅可比矩阵的性质，使它在求解这一方程时，具有很高的效率，其求解效率几乎是高斯法的两倍，并且可以很好的与数据压缩算法共同工作。
　　3.共轭梯度法是是解线性方程组迭代解法中较好的一种，其算法稳定收敛快，并且可以进一步节省内存，当管网的规模超大，直接解法不能运算时，它是一种很好的补充；在一般规模的管网下，也可结合直接解法，使迭代的速度加快。
2.2牛顿步长因子的改进
　　牛顿法是求解非线形方程组的一个经典方法，由于其收敛快，因此直到现在它仍然是一个重要方法，很多新的算法都是对它的改进。但它的问题也是很明显的，就是当初值选择不好时，它有可能不收敛。而初值的选择往往具有随意性，这样计算往往是发散的。
　　为解决这一问题，迭代公式中加入步长因子λ，这样迭代公式就变成了

　　E_new=E_old+λδE

　　步长因子λ控制迭代收敛的速度也影响着模型是否收敛，本文作者通过对步长因子λ的处理使整个迭代过程即保证收敛而且收敛较快。
2.3数据的压缩存储
　　供水管网方程的连续性方程的雅可比矩阵的阶数是很高的。计算数据占用的计算机内存非常惊人的，如果不对雅克比矩阵进行压缩，可能将导致计算不能进行。同时该矩阵具有对称性、正定性、带状性、稀疏性的特点，进行矩阵压缩是可行的。通过对矩阵的压缩也可使参与计算的数据量减小，从而提高计算的速度。作者采用的是一维变代宽存储压缩技术。
2.4优化带宽
　　用一维变带宽算法存储雅可比矩阵，矩阵的带宽和节点的编号有关，管段的起止节点编号差越大，雅可比矩阵的半带宽也越大，解方程组的效率也越低，如果带宽太大而导致三角块无法存储，求解也就无法进行。为了提高解方程的效率，在进行节点编号时，要使节点差尽量的小。但如果这部分工作用手工完成，将花费大量的精力。所以要采用自动编号来对带宽进行优化。
本文作者采用有限单元理论中的优化编号方法，自动进行节点编号，对带宽进行优化。使数据的存储量变到最小，对提高计算速度起到十分明显的作用。
2.5管网简化
　　前面提到供水管网连续性方程的阶数是很高的，求解这一方程的计算量和阶数的立方成正比，也就是说如果管网中节点的个数增加到原来的2倍，其计算量几乎增加到原来的8倍，因此如何能等效简化管网是一个非常有意义的课题。
　　1．支状管网简化。供水管网中有许多支状管网，根据流体力学的计算理论，这些管段完全可以简化掉，而且并不影响管网模拟计算的精度。
　　2．环状管网简化。环状管网简化比较复杂，会导致一定误差。在允许误差范围内简化环状管网是一个很新的课题。国外有些研究单位可以将一个复杂管网简化到只有几十个节点的程度，误差还不大，这种技术主要应用在优化调度领域。
本文作者通过编写计算机程序实现了对管网数据自动进行支状的简化。这种简化不影响计算结果，当管网中支状管数量较多时，通过这种处理后，水力模拟计算速度的提高是十分明显的。
2.6管网数据检查
　　平差计算时，录入数据常常发生错误，如编号错误、遗漏节点管段等，这将直接直接影响导致网络拓扑结构的变化，当网络很复杂，查找错误将变得很困难，因此编写了自动检查错误程序。
　　供水管网的拓扑结构是一张图，用图论中图的遍历算法可发现图纸中拓扑结构的错误。通常有两条遍历图的路径，深度优先搜索和广度优先搜索。本文作者采用的是深度优先搜索算法。
2.7数据结构的优化
　　进行上诉算法的优化必须以较好得数据结构为基础，作者编写的计算程序中用面向对向的编程方法对数据结构实现了动态描述。通过这种数据结构的建立，可实现对数据的快速排序和查找，并能保证上诉优化算法快速实现。
除此以外，计算程序中添加了计算结果的汇总分析功能，可生成详尽的结果报告。

3计算结果检验

3.1计算结果的正确性检查
　　为验证计算结果的正确性，用3个相同的算例，不同的程序对它进行了计算，对计算结果进行了比较，其计算结果符合的非常好。这3个算例，一个是自己设计的(53个节点，78条管段)；一个是公主岭的管网(312个节点，386条管段)；一个是天津市供水管网(3435个节点，4498条管段)。选用的对比程序有3个，一个是LOOP(世界银行贷款资助的软件);一个是WM5(国外知名水力模拟软件，全名WaterMan ver5.0);另外一个是国内的一个优秀计算软件WQR。计算结果之间的差别是很小的，主要是选取有效数字位数不同或采用的计算公式不同造成的。

数据 WQR WM5程序 Loop程序 小例子 0.1% 0.1% 0.4% 公主岭管网 0.2% 0.2% 0.5% 天津管网 0.4% - -

3.2优化编号的作用
　　对于前两个算例，计算速度很难进行比较，因为计算的时间太短了，但采用共轭梯度法的计算程序，在管网规模不是很大时，其计算计算速度十分快，原因是方程阶数低造成的管网初值与正确解比较接近，使共轭梯度法的收敛速度得到充分的发挥。管网规模扩大时，由于LOOP和WM5都不能求解，所以只能与WQR程序进行对比。计算天津管网，WQR程序需要150秒，而这个程序只需要22秒。速度的提升是明显的，而且在理论上，管网的规模越大，其速度比将越大。

项目 优化编号前 优化编号后 计算时间 122 22

3.3支状管网简化
　　支状管网简化的效果根据网络的拓扑结构的不同而不同。由于数据结构的优化，进行简化的过程很短，对于天津这样大型的管网花费的时间在0.5秒左右。

数据 原计算节点数 简化后计算节点数 计算速度提高率 小例子 49 49 0 公主岭管网 290 216 30% 天津管网 3435 2645 18.5%

　　支状管网的简化可以进一步缩小总带宽，以天津管网为例，简化后其总带宽由20万左右缩小为15万左右，使计算速度进一步提高，由22秒减少到不到18秒。
3.4计算时间对比
　　通过对算法的多方面优化，系统计算速度得到明显的提高，与测试程序相比较其计算速度都有较大的优势。

数据 本程序 WQR程序 Loop程序 WM5程序 小例子 0.05 0.77 1.5 0.51 公主岭管网 0.11 2.12 10 1.44 天津管网 17.93 150.22 - -

　　(以上测试均是在联想Pentium 300内存64M的笔记本计算机上完成的。)

---

作者简介：
魏宝成 讲师 哈尔滨工业大学市政环境工程学院
通 讯 处： 150090 哈尔滨工业大学（二区）624#信箱
电话：0451-6282281
Email:[email protected]