城市供水管网改扩建优化方法的研究

刘小静 许仕荣 谢社平 何元春
（湖南大学土木工程学院水科学与工程系，长沙410082）

　　摘要 为克服一直以来城市供水管网系统改扩建优化工作的改造布局和离散管径优化的两大难题，本文采用模拟退火的玻尔兹曼机这一神经网络技术进行求解，直接得到了市售管径和优化的改造布局；整个系统采用系统工程的分解协调法来优化。
　　关键词 供水管网 改扩建 优化方法

　　Abstract This paper adopts neural network technique of Simulated Annealing’s Boltzmann to solve the twain hang-ups in the rebuild and extend optimum work of city flow network since all along － the optimum of rebuild layout and scatter pipe-span. Then we can get the twain optimum results directly. Whole economy can be optimized by decomposing and corresponding divisor of systems engineering.
　　Key words flow network rebuild and extend optimum method

　　1．前言

　　随着我国给水事业的迅猛发展，各地市给水管网已具规模，但随着人口增长和生活水平的提高，城市用水量急剧增长，管网系统满足不了增长的用水量，在各方面存在一系列问题，从而适时、科学地对现有给水管网进行改扩建优化设计的研究，是城市供水行业亟待解决、有较高经济效益和社会效益的课题。
　　供水管网系统改扩建优化设计问题，是在新建管网优化技术的基础上更为复杂的含有混合整型离散变量的非线性规划问题。以往的方法通常是在设计人员以经验确定管线布局的条件下，采用连续变量的约束非线性优化方法求解该复杂的目标函数，再由连续最优解上下取整或通过目标函数转换由连续变量优化方法求解。混合整型离散优化问题的特殊性使这种求解方法难以获得原目标函数的最优解。
　　值得一提的是，改扩建又不同于新建，研究的不只限于新建管网的优化，其目标函数中也包含了旧有管段的因素，即有某些旧有管段的不合理存在，大大影响了整个管网的运行费用。从节能的角度，在扩建管段寻优的同时，要对不合理的旧管段进行改造，这势必要增加基建投资（改造措施采用增敷平行管线的方法），那么其需要解决两个问题：①在什么地方敷设新增管道；②增敷管线的经济管径怎么确定。这就存在一定的困难，主要表现在：①初始管网布局的确定比较困难；②人的经验知识不易总结；③由于经验知识的局限性，不易找出问题的最优方案。而扩建设计中新旧管道交错，流量分配的作用非常复杂，用常规方法求解更是困难重重。从而如何对改造管道的布局寻优，如何在充分利用原有管道供水能力的情况下，对需改造、扩建的管网进行优化，比新建设计更为复杂，又是一道急需解决的难题。
　　给水管网是一个复杂系统，单凭市政工程的专业知识，不能圆满地解决管网水力分析和设计运转问题。在众多的研究工作中已引入了其它学科的研究成果，如数学规划、图论、计算技术、最优控制、自动化、系统工程等，这样可拓宽分析方法和研究范畴，发展新的理论和方法。

　　2．供水管网改扩建数学模型和计算方法

　　2.1 供水管网改扩建数学模型的建立
　　城市供水管网改扩建的优化设计问题，是在系统设计年限内最高日最高时用水量Q_i( i=1,…,m )已知的情况下，确定新增（改造）管道的布局x_ij(i , j∈V)和参数D_ij(i , j∈V)，并确定各水源的供水量u_i (i∈S)，各节点的压力H_i(i = 1,…,m)使得总的供水成本尽可能低。该优化设计问题的非线性规划模型可归纳为：

　　min f ( H, D, x, u, Hp)

　　

　　s.t. g_i ( H, D, x, u, Hp) = 0 i = 1,…,m-1

　　

　　

　　H_i≥H_i^min 　　　　i = 1,…,m

　　u_i-u_i^min≥0　　　　i∈S

　　u_i^max-u_i≥0　　　　i∈S

　　D_ij∈W　　　　 i , j∈V

　　HP_ij≥0　　　　　i , j∈V

　　

　　式中：

　　D — 管径（米）
　　l — 管线长度（米）
　　T ,T＇, T＂— 管线、泵站、水厂的投资偿还期（年）
　　P ，P＇，P＂—管线、泵站、水厂的折旧与大修理费（%）
　　V—可布置改造和扩建管线位置的集合
　　a,b,α — 造价公式中的系数和指数， 随管线材料和施工条件的不同而异
　　r_i — i期供水能量变化系数，i = 1, 2, 3 分别表示供电高峰期、正常期和低峰期
　　E_i — 供电i期电价（元/kw.h）
　　T_i — 供电i期供水时间(h)
　　u_{i j} ,η_{i j} — 分别为供电i期第j送水量(l/s)和泵站效率(%)
　　h_i,j,k — 供电i期第j送水泵站至管网控制点管线上k管段的水头损失(m)
　　Z_C — 管网控制点要求的自由水压值(m)
　　Z_K — 净水厂至管网控制点的某条线路的管段集
　　S — 所有泵站个数
　　E＇—每千瓦容量加压泵站造价（元/kw）
　　r＇— 泵站机组储备系数
　　η＇— 泵站与输电线效率（%）
　　mp — 泵站基建造价的经济效应系数0＜mp≤1
　　C_K、C_N — 分别为改建、扩建单位水量净水厂（送水泵站）所需基建费用（元/ l/ s）
　　R_K、R_N—分别为改建和扩建净水厂集
　　u_0i— 第i净水厂送水泵站原有最大供水量(l/s)
　　mr—净水厂送水泵站基建经济效应系数0＜mr≤1
　　2.2 供水管网改扩建的计算方法
　　改扩建这个复杂的课题可用系统工程的大系统分解分层协调的方法分解成四个相关的子问题进行求解（其流程图如图1所示）：

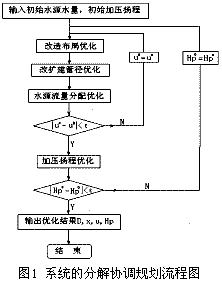
　　①在水源供水量和加压扬程给定的情况下，对旧管网改造布局的优化子课题。它不同于新建模型优化的一点是，它的目标函数费用值不能计入整个系统的目标函数费用值中。

　　min f (H, D, x)

　　s.t. g_i ( H, D, x) = 0 i = 1,…,m-1

　　H_i≥H_i^mini = 1,…,m

　　D_ij∈ W 　　　　　i , j∈VV

　　X_ij=0,1　　　　　 i , j∈VVV

　　②若将u及Hp固定，节点数m不变，管径数为需改造的管径数及新建管径数之和，此时旧管网改造布局的变量x_ij 已求得；则需改造和扩建管网的管径优化子课题为：

　　min f ( H, D)

　　s.t. g_i (H, D ) = 0 i = 1,…,m-1

　　H_i≥H_i^min　　　　　 i= 1,…,m

　　D_ij∈ W　　　　　　 i, j∈V

　　③设旧管网、需改造的管网及新建管网的集合为N；若将x，D及Hp固定，节点数m不变，管径数为旧管径数、需改造的管径数及新建管径数之和；则水源流量的优化子课题为：

　　min f (H, u )

　　s.t. g_i ( H, u ) = 0 i= 1,…,m-1　

　　H_i≥H_i^min i = 1,…,m

　　u_i-u_i^min≥0 　　　i∈S

　　u_i^max-u_i≥0 　　　i∈S

　　④若将x，D及u固定，节点数m不变，管径数为旧管径数、需改造的管径数及新建管径数之和n；则加压扬程的优化子课题为：

　　min f ( H, Hp )

　　s.t. g_i ( H, Hp ) = 0 i = 1,…,m-1

　　H_i≥H_i^mini = 1,…,m

　　HPij≥0　　　　　　i , j∈V

　　3. 改扩建改造布局和管径优化的模拟退火的玻尔兹曼机解法

　　3.1 模拟退火的玻尔兹曼机法简介
　　从简单的数学角度来求解改造布局和管径优化的课题至今仍为管道技术的一大难关，而八十年代兴起的人工神经网络方法，在解决非线性优化问题上显示的强大生命力，也给城市供水管网系统课题提供了新的启示。
　　人工神经网络是由大量简单的神经元构成的并行分布处理系统。此问题实质上是在满足一定约束的条件下，在并行分布处理网络中搜寻最佳解的问题。对此，对Hopfield神经网络赋予部分记忆矢量（部分约束）作为初值，网络运行就达到某个局部最小点。该网络中任何一对神经元之间的信息传输是双向对称的，它的基本工作原则是对网络设置一个描述其状态的能量函数E，该能量函数在系统状态改变时总是减小，即dE≤0，系统必会到达一稳定点，其能量函数代表总花费。Boltzmann机神经网络模型是在Hopfield网络基础之上引入随机机制而形成的，具有较强的计算能力。与Hopfield网络不同的是它具有学习能力，即其权值通过学习来调整，而不是预先设置，是一种约束满足神经网络模型。
　　模拟退火的Boltzmann机解法是在Boltzmann机中随机地选择一处理单元，通过系统状态的改变，使系统的能量函数E朝其减小的方向递减到一个稳定状态，这个状态往往是能量函数E的一个局部极小点，而达不到全局最优；再引入模拟退火算法，使整个系统产生振动，引导网络达到其最佳平衡态，这就是搜索的最优解。
　　3.2 引用Boltzmann机进行改造布局和改扩建管径优化的处理要点
　　①决策变量的转换及神经元集合的构成
　　由于Boltzmann机的神经元状态只能取0和1两种状态，需将独立变量转换成0-1变量。由于x本身就是0-1变量，无需转换，只要将变量D转换成0-1变量。对离散变量D，若它在集合W中可取的市售型号有M种,D的第ij维分量D_ij用二进制字符串表示的最少符号个数m为2^m≥M，D_ij的取值与字符串S1^＂ΛS2^＂的取值一一对应。否则，若2^m>M，字符串的取值多于D_ij的取值，这时可以将多余的字符串的取值再对应于D_ij的部分取值，使得每个字符串的取值对应的D_ij的取值均是可行的。将D分量加上x分量构成神经元集合S。对于每一个S_i^j∈S，S_i^j∈{0,1}，且S中的神经元元素的个数nl为 。
　　②能量函数
　　根据Boltzmann机的基本原理，改造布局或改扩建管径优化的能量函数构造为。
　　式中：E—改造布局或改扩建管径优化的能量函数
　　　　　f₁—改造布局或改扩建管径优化的目标函数

　　

　　A 一适当选取的正罚系数

　　③温度T减小方式及计算过程的终止判据：在最优解的搜索过程中，温度T由高温逐渐降至低温，其温度T减小方式为T =λT，0 <λ< 1，根据经验，笔者建议取λ= 0.8。当T → 0，即T＜ε（ε是一小的正数）时，搜索最优解的过程结束，计算过程终止。
　　④状态转移的终止方式
　　在给定的温度T，要进行多次搜索即状态转移，其状态转移方式为先以均匀分布在神经元集合中选择一个单元，然后将其状态作转换，即若原来的取值为0，现在将其取为1，反之将其取为0。
　　⑤状态转移的终止判据
　　判断状态转移是否结束可以有多种方法，如a) 检验目标函数值的均值是否稳定；b) 连续若干步目标函数值的变化均比较小；c)按一个固定的步数L进行状态转移等。这里选择采用方法c)
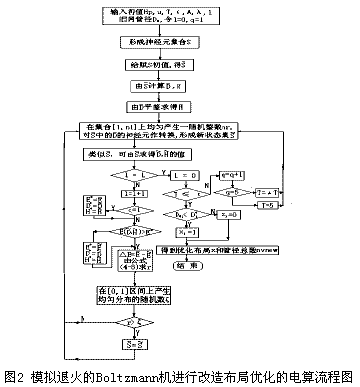
　　3.3 Boltzmann机进行改造布局优化的电算方法
　　其方法是在优化结果中分析旧管网，如果计算管径比实际管径大，则考虑增敷一平行管线，即x的值取为1；否则，原有旧管径处不变，即x的值取为0；并得到新的整体系统的总数（原有旧管径、新建管径和需改造管径之和）。
　　值得注意的是，由该优化子课题得到的有用的结果只是需改造的旧管径的地点，即改造布局优化，并不使用它求得的优化管径。该优化子课题不参与总费用值的计算。其电算框图如图2所示。

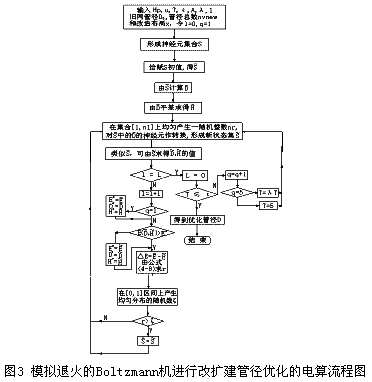
　　3.4 Boltzmann机进行改扩建管径优化的电算方法
　　对于改扩建管径的优化，其原理与改造布局优化一样。它根据布局优化子程序输入的管径总数和改造布局，在原有旧管径不变的情况下，求新建管径和需改造管径的优化结果。该子程序中，变量x为已知量，神经元集合S中只有神经元D。从而可得利用模拟退火的Boltzmann机进行改造布局优化的电算流程图3。该算法计算获得的并不一定是问题的全局最优解，但它是一个非常接近其全局最优解的局部最优解，其原因是：①由算法本身的特性决定的，该算法是以概率1保证其收敛到它的局部最优解，而不一定是全局最优解。②神经元的构造方法，包括编码及精度，对算法的计算效果有一定的影响。

　　3.5 不同负载状态下的布局和管径的优化
　　在不同负载状态下的布局和管径的优化设计，采用模拟退火的Boltzmann机算法仍是易行的。当网内存在水塔水库时，其运行上存在两种状态：①高峰用水期，水源和水塔水库同时供水；②低谷用水期，单由水源供水并向水库充水。此时，管线布局和管径的计算要按高峰用水时和最大传输时的二种负载进行。所以，该优化设计计算子规划目标函数为：

　　

　　s.t. g^/_i ( H₁, D, x , u₁ ) = 0 i = 1,…,m-1

　　g_i ( H, D, x , u ) = 0 i = 1,…,m-1

　　H_i≥H_i^min　　　i = 1,…,m

　　H_i1≥H_i1^min i = 1,…,m

　　D_ij∈ W　　　　　i , j∈VV

　　其中：H, Q ——最大转输时管网的节点压力和节点流量
　　　　　H₁, Q₁ ——高峰用水时管网的节点压力和节点流量
　　　　　H_i^min，H_i1^min——分别表示最大转输时和高峰用水时管网各节点的最小允许压力
　　 　　g^/, g — 分别表示最大转输时和高峰用水时管网的节点方程组
　　 　　S — 最大转输时水源二级泵站个数
　　　　S₁ —高峰用水时共同工作的二级泵站和水库的个数
　　 　　C_r，C_r1 — 分别包含能量变化系数v和 v₁　　v —— 年平均耗电能对最大转输时耗电能的比例
　　　　v₁ — 年平均耗电能对高峰用水时耗电能的比例

　　关于它的算法，只需在前述算法中做一些改动：
　　①水源水量分配的初值为最大转输时u和高峰用水时u₁两项；
　　②在由D, u求H的同时，也由D , u₁ 求得H₁；
　　③能量函数改为

　　

　　这些改动表示D的变化必须兼顾二种负载状态下动力费用的变化，通过能量函数的稳定可求得有效的结果。

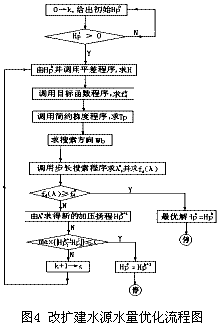
　　4　改扩建水源水量和加压泵站的优化方法

　　在改扩建管网设计中，因用水量增长必须增加水源的供水，由此产生了水厂供水的分配问题：①是否需要开辟新的水源；②如果需要新建水厂，新、旧水厂的供水量如何分配；③如果不需要新建水厂，在旧水厂之间如何分配这部分新增的水量。最优方案的选择应使管网的常年动力费用（以发挥最大生产能力时的动力费用折算成年平均费用）和新建或扩建水厂所需的基建费用之总和为最小。
　　此外，由于给水面积扩大，用水需求加大，管线延长，管路的水头损失将增加，为了保证边缘地区的水压，节约动力费用，管网内往往设置加压泵站或水库泵站。加压泵站的优化设计就是研究如何选择加压泵站的个数、位置和加压扬程使得管网的动力费用和新建加压泵站的基建造价和为最小。
　　为解此两大型优化方程组，考虑了几个较为适用的主要优化算法：Mpop法解题的成功率很高，但寻找可行点的功能还不完善；Mulpen法有效性指标还不很令人满意；GRG性能好，适应性强，解题成功率比较高，对于退化的全等式线性约束问题处理不好，但GRG法原理较复杂、算法庞大，对于大型优化问题有着较好的针对性。因而考虑用GRG算法来解决该数学模型是比较理想的。此两个子课题的电算流程图如图4和图5所示。

　　

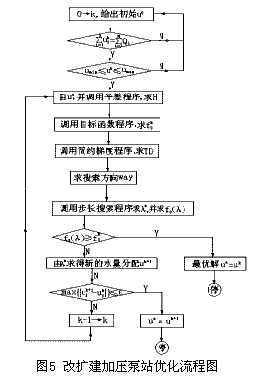
　　5. 工程应用与总结

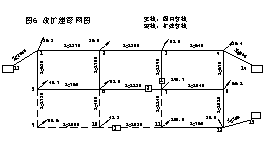
　　利用以上算法对长沙自来水公司的课题进行改扩建仿真计算；现以一简例说明，如图6所示。其计算过程列为表1。由计算结果可以看出，上述计算过程获得了问题的全局最优解。对大规模的供水管网系统，该分层算法有显著效果。

表1 改扩建仿真计算结果表 管段d 原有管径 布局X 增敷管径 1-2 0.45 1 0.50 2-3 0.30 1 1.30 3-4 0.45 0 4-8 0.10 1 0.20 5-6 0.10 1 0.10 6-7 0.30 1 7-8 1.30 0 9-10 0 1 0.10 10-11 0 0 11-12 1.30 1 1-5 0.10 1 0.10 2-6 0.35 1 0.10 3-7 0.40 1 0.10 5-9 0 0 6-10 0 1 1.30 7-11 0 1 1.30 8-12 0.10 0 水源 13 14 15 水量(l) 0.417 0.405 0 加压泵站 1 2 3 扬程(m) 14 0 0

　　6. 参考文献

　　[1] B.Coulbeck,Dynamic Simulation of Water Distribution Systems, Mathematics and Computers in simulation,1980,Vol.XXⅡ,222-230
　　[2] L.Gyergyek and S.Persen,Simulation and Optimal Control of Large Water Distribution Systems, Mathematics and Computers in simulation,1982,Vol.XXⅣ
　　[3] Neural Networks Based Decision Support in Presence of Uncertainties, Journal of water Resources Planning and Management,1999,No.5
　　[4] E.Aarts and J.Korst, Simulated Annealing and Boltzmann Machines,John Wiley & Sons,1989
　　[5] 全国供水管网论文集，1998
　　[6] 许仕荣，邱振华，给水管网的计算理论与电算应用，湖南大学出版社，1997
　　[7] 俞国平，给水管网扩建工程的最优化设计，同济大学博士论文，1985
　　[8] 颜虎等，改造旧管网扩建方案可行性研究的方法，中国给水排水，1991
　　[9] G.V.雷克莱狄斯等，工程最优化—方法与应用，北京航空航天大学出版社，1990
　　[10] 陈立周等，工程离散变量优化设计法—原理与应用，机械工业出版社，1988
　　[11] 熊光楞，连续系统仿真与离散事件系统仿真，清华大学出版社，1987
　　[12] 仲伟俊，供水网络系统改造的智能化计算机辅助设计，信息与控制，1995，6
　　[13] 李卫华，人工智能程序设计，科学出版社，1989
　　[14] 胡守仁，神经网络导论，国防科技大学出版社，1993
　　[15 胡守仁，神经网络实现技术，国防科技大学出版社，1993
　　[16] 胡守仁，神经网络应用技术，国防科技大学出版社，1993
　　[17] 陈伟民，人工智能技术及应用，同济大学出版社，1998
　　[18] 万百五等，大工业过程计算机在线稳态优化控制，科学出版社，1998

---

　　作者简介：
　　刘小静（1975- ），女，湖南人，
　　电话：(0731)8828281
　　通讯地址：湖南大学研究生楼501室 410082>

　　注：该课题为长沙市自来水公司公关项目。