给水系统多目标混合实用优化调度方法

吕谋¹，张土乔¹，赵洪宾²

（1.浙江大学 市政工程研究所 2.哈尔滨工业大学 市政环境工程学院）

　　摘要：根据给水系统的网络特性，并结合我国实际情况，对优化调度控制方法进行了系统的分析，进而提出了大规模混合实用优化调度模型及算法，并在城市供水系统中进行了实际应用，证明了其实用性。
　　关键词：给水系统；混合优化；实用调度
　　中图分类号：TU991
　　文献标识码：A
　　文章编号：1000-4602(2000)11-0010-05

Multi-Purposes Mixed Optimal Operation Schedule for Water Supply System
LU Mou¹,ZHANG Tu?qiao1,ZHAO Hong?bin²
(1.Institute of Munic.Eng.,Zhejiang Univ.,Hangzhou 310029,China;2.School of Muni
c.and Environ.Eng.,Harbin Institute of Tech.,Harbin 150090,China)

　　Abstract： According to the network characteristics of water supply system and the practical situation in China,an optimal operation schedule in water distribution networkwas analyzed,and then a practical mixed d- ispatch model and algorithm on large scale water supply system were put forward.The model was applied to urban water supply system and verified its practicability.
　　Keywords: water supply system;mixed?optimization;operation schedule

　　1 模型分析

　　优化运行控制问题就是为已定的配水系统提供科学合理的优化运行策略。根据所选决策变量的不同,可以建立供水系统决策的隐式模型和显式模型^［1］。显式模型中直接以实际水泵的运行作为决策变量；而隐式模型则是首先采用中间变量，如泵站、出口流速、水池变化轨迹等，并依此进行目标函数的寻优。隐式模型的求解精度较高，优化效果好，但计算耗时很长，对于泵站内水泵组合数较少，缺少调速泵，即泵站内可调余地较小的系统，有时得不到优化解。因为当一级寻优得到最优的流量分配后，泵站内有限的水泵组合种类不能满足所需要的供水流量，就可能使泵站组合种类的可行域与最优流量可行域的交集出现空集，即出现无解的情况。显式模型由于将整个系统统一考虑，一次求解，计算效率较高，但一次建模中考虑的变量及约束条件多，建模及运行复杂，当供水系统中的泵站可调余地小，寻优困难时，可考虑放松系统约束条件，以满意解为追求目标，建立显式优化决策模型，以保证优化调度的可行性。

　　2 定速泵站优化调度模型的建立

　　给水系统优化调度的目的，就是通过调整运行方案，在满足水量、水压要求的前提下，尽量使系统总运行费用达到最低^［2］。那么随调度方案的不同而发生变化的这部分运行费用主要包括∶(1)制水成本 (2)泵站电耗。优化调度建模一般需要构造目标函数和约束函数，目标函数是指系统运行需达到指标的数学描述，即数学表达式；约束函数是指制约或控制系统运行的数学表达式，即优化运行必需满足的前提和基础。通常，供水系统优化调度模型是以运行费用为目标函数，以满足管网水力特性方程及其他技术条件为约束进行系统整体优化的，因此目标函数应包括：
　　① 制水成本
　　由水厂药剂费用及取水和净水过程耗用的电费。数学描述为：

　　

　　式中　F₁——制水成本
　　　　　S_i,j——第i泵站第j时段单位制水费用(元/m³)　
　　　　　Q_i,j——第i泵站第j时段的出水量
　　　　　I——水源泵站数
　　　　　J——划分的周期内时段数
　　② 泵站电耗
　　在计费计算中，一般只计直接费用，不计间接费用。可描述为：

　　

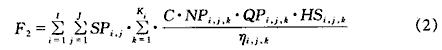
　　式中　SP_i,j——第i泵站第j时段的电度电费
　　　　　C ——换算系数
　　　　　NP_i,j,k——第i泵站第j时段第k种水泵开机台数
　　　　　QP_i,j,k——第k种泵出水流量
　　　　　HS_i,j,k——第k种水泵出水扬程，可由Q～H特性曲线拟合其关系式
　　　　　η_i,j,k——第i泵站第j时段第k种水泵的计算效率，可由水泵效率曲线拟合其关系式
　　　　　K_i——i泵站水泵型号种类数
　　考虑供水系统运行的技术要求及为了更好地与实际系统相吻合，可考虑建立多目标优化调度模型，则技术目标包括：
　　① 供需水量差F₃最小

　　

　　式中　QF_j——j时段系统的总需水量(由用水量预测模型计算求得)
　　实际供水系统中，供需水量是平衡的，即：，也就是说，这应是优化模型中的一个硬约束条件。但为保证优化计算的可行性，可以将其软化，放松约束限制，以扩大可行域，因此本文将，也作为优化追求的目标，在优化过程中逐步使_,逼近QF_j，最终得到优化目标的可行满意解。实际应用发现，这种处理使优化程序的通用性及可靠性大大提高，是一种有效的实用方法。
　　② 泵站供需压差F4最小

　　

　　H_i,j为第i泵站第j时段满足配水管网用水量所需要的泵站出口压力，其计算值可通过对供水网络的运行分析，建立管网工况动态非线性模型得到，
　　即：H_i,j=F(Q_j,H_P,j)　　　　　　　　　　　(5)
　　式中　　Q_j——j时段各出水泵站的出水流量所组成的向量
　　　　　　H_P,j——各测压点按时间序列分析所得到的压力预报值向量
　　HP_i,j为第i水泵站第j时段能提供的出水水头，其计算式由泵站内各水泵联合工作的Q～H特性曲线拟合得到。实际运行的供水系统，应满足供需水压相等，即：H_i,j=HP_i,j，是优化模型中的硬约束条件，但由于与F₃相似的原因，这里也将其软化，以作为优化追求目标，在优化过程中逐步使H_i,j逼近HP_i,j，最终得到优化目标的可行满意解。
　　根据给水系统的特性，优化调度模型时还需要考虑约束条件，对于上述多目标决策问题，可采用多种优化方式，这里提出化多为一的乘除法，将多目标转化为单目标问题求解。则建立城市供水系统的显式优化调度模型如下：

　　

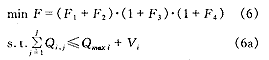
　　H_mini,j≤H_i,j≤H_maxi,j 　　　　　　(6b)
　　HS_mini,k≤HS_i,j,k≤HS_maxi,k 　　　 (6c)
　　QS_minj,i≤Q_i,j≤QS_maxj,i 　　　　　(6d)
　　NP_mini,k≤NP_i,j,k≤NP_maxi,k 　　　 (6e)

　　式中　N——测压点数
　　　　　V_i——第i泵站调度日开始时段的储水池有效储量
　　　　　Q_maxi——一日内最大出水量
　　　　　H_mini,j——第i测压点j时段最低运行服务水头
　　　　　HS_mini,k——第k种水泵最低供水扬程
　　　　　HS_maxi,k——第k种水泵最高供水扬程，它们是由水泵特性曲线的高效区决定的
　　　　　QS_minj,i——i泵站j时段最低允许供水量
　　　　　QS_maxj,i——i泵站j时段最高允许供水量
　　　　　NP_mini,k——第i泵站第k种水泵最少开机台数
　　　　　NP_maxi,k——第i泵站第k种水泵最多可运行数量。
　　所谓显式调度模型是将整个给水系统结合在一起建模，经一次寻优直接得到最优的水泵运行决策方案。模型（6）中的目标函数中含有多个连续变量及离散变量，实际计算时，这里仅取HP_i,j及NP_i,j,k作为寻优决策变量，其他连续变量可以由它们解出。
　　Q_i,j求得后，利用式(5)可确定H_i,j。由此可见，当HP_i,j及NP_i,j,k确定后，其他变量便可唯一求得，因此式(6)可概括成：
　　min　F(NP_i,j,k，HP_i,j) 　　　　(7)
　　s.t. g(NP_i,j,k，HP_i,j)≤0
　　对于这种含有连续变量又含有离散变量的优化问题，我们在以离散搜索法为理论依据的MDOD方法^［3］的基础上，经改进开发了求解混合离散变量的供水系统直接优化调度软件（用C++计算机语言），程序计算框图(见图1)。

　　3 多水源含调速泵的优化调度

　　变速调节虽然是较为理想的调度形式，但相对于水泵价格而言，调速装置的价格是昂贵的。因此，为了节省一次投资，经常采用恒速泵与调速泵并联的方式，尤其是针对目前的国情，很多城市的二级泵站还没有装配调速装置，因此混合泵站的优化调度具有很现实的意义。
　　由于与定速泵站相比，混合、变速泵站的可调余地大，应该对定速泵站和混合、变速泵站采取不同的处理方法，这里提出将隐式模型与显示模型相结合，建立混合实用优化调度模型。为研究方便，设系统中含有定速泵站和混合泵站两种类型(含有变速泵站的情况可参照混合泵站的情况解决)。即编号1，2，…，X为定速泵站，X+1，…，I为混合泵站，参照式(7)仍可建立混合供水系统调度运行的直接优化模型。其优化追求的目标仍然由F₁、F₂、F₃、F₄组成，设：[NP_1,j,k,NP_2,j,k,…，NP_X,j,k］^T=NPF,［QP_1,j,k,QP_2,j,k,…,QP_X,j,k］^T=QPF,［Q_X,j,Q_X+1,j,…，Q_I,j ^T=QV(j=1,2,…，J；k=1,2,…，K_i)
　　则：F₁=∑Xi=1∑Jj=1S_i,jQ_i,j+∑Ii=X+1∑Jj=1S_i,jQ_i,j　　　(8)
　　由于Q_i,j＝∑Kik=1NP_i,j,k·QP_i,j,k 　　　　　　　　　　　 (9)
　　式(8)等号右边第一项由式(9)代入，第二项保持不变，即：
　　F₁=FF₁(NPF,QPF)+FV₁(QV)　　　　　　　　　　　　　　　　　(10)
　　F₂式也可分成两部分
　　

　　式中　H_i,j——第i混合泵站第j时段泵站出口压力
　　由式（5）可表达成各泵站出水流量的函数，则上式可表达成：
　　F₂=FF₂(NPF,QPF)+FV₂(QV,NPF,QPF)　　　　　　　　　　　　 (12)
　　结合式(9)，混合系统的技术性指标F₃可表示成：

　　

　　对于调速或混合泵站，在调节范围内，对应于每一个配水管网所要求的泵站出口压力，总可以通过调整调速泵的转速使泵站供水扬程满足管网需要，也就是说在满足供水量的前提下，保证供需水压平衡。在直接优化调度模型中，只把混合泵站的出口压力及出水量作为决策变量来考虑，也就是说，寻优结果只是得到混合泵站的最优出水量及最优出水压力，并没有实际泵站内的实际运行策略，因此不存在供需水压差最小这个指标。则F4可表达成：

　　

　　则混合供水系统的直接优化调度模型可表达成：
　　min F=(F₁+F₂)·(1+F₃)·(1+F₄) 　　　　(15)

　　
　　H_mini,j≤H_i,j≤H_maxi,j(i=1,2,…，N；j=1,2,…，J)
　　HS_mink≤HS_i,j,k≤HS_maxk(i=1,2,…，X；j=1,2,…，J；k=1,2,…,K_i)
　　QS_minj,i≤Q_i,j≤QS_maxj,i(i=1,2,…，I；j=1,2,…，J)
　　NP_mini,k≤NP_i,j,k≤NP_maxi,k(i=1,2,…，X；j=1,2,…，J；k=1,2,…,K_i)
　　上述数学模型含有连续变量(如：Q_i,j,k,HS_i,j,k)及离散变量(如：NP_i,j,k)，对于这种既含有连续变量又含有离散变量的优化问题，我们在以离散搜索法为理论依据的MDOD方法^［3］的基础上，经改进开发了求解混合离散变量的供水系统直接优化调度软件（用C++计算机语言），寻优结果可以直接得到1～X个泵站的运行策略，即各泵站内各种水泵的开机台数；另外X+1～I个混合泵站，只得到泵站的最优出水流量Q_i及最优出水水压H_i。对于这种出口流量及出口水压已给的混合泵站优化调度问题，需对泵站内的水泵进行优化组合并确定调速泵的转速，即二级寻优^［4、5］(由于篇幅所限，具体的求解方法另文介绍)。

　　4 实际应用

　　沈阳市日供水量达150×104 m³以上，其大小供水泵站总和有31个之多。通过对沈阳市供水系统各供水泵站的逐一分析,剔除这些供水量很少及供水量变化不大、可调余地很小及相对独立的供水泵站，主要针对在调度及工况建模中具有实际意义的十个泵站进行研究，掌握了各泵站的水泵机组情况及水池的可调容积。沈阳市自来水公司根据沈阳市用水特点，通过多年的运行管理，摸索出了许多调度管理的经验。他们将一天24 h分成五个各有特点的时段，分别进行调度控制，具体为：①0：00～5：00，早低峰；②5：00～8：00，早高峰；③8：00～17：00，中峰；④17：00～20：00，晚高峰；⑤20：00～24：00，晚低峰。在对沈阳市的优化调度中，以该时段划分为基础，提出各时段的优化调度决策方法。
　　沈阳市的供水系统主要是由定速泵站组成，另有两个混合泵站(大伙房和新北陵泵站)，因此它属于混合供水系统。因其供水特点较复杂，在高峰用水时有些小井泵站直接向管网供水，但水量小，难管理，不能参与调度；并且有时为限量供水，人为关启管网及泵前阀门，这就给管网的工况建模增加了很大难度。另外，各供水泵站主要由定速泵组成，且水泵型号较为单一，有的泵站只有一种型号，并且有的泵站必须满负荷运行，没有多少可调余地，若采用隐式模型(进行分级优化调度)，则在寻优过程中，可能出现无解现象。因为如首先进行供水量的寻优，再进行泵站运行决策优化，则由于有些泵站可调余地较小，可能得不到可行解而使寻优中断，由对其进行的实际测算，也证明了这一论断。若采用式(15)的混合模型，将水源、泵站与管网有机地结合起来，从安全供水、经济运行及供水可行性的角度出发，将含调速泵的混合泵站与定速泵站区别考虑，充分利用其各自特点，合理调配各种水泵，以达到系统整体最优，则更适合沈阳市供水系统的现有条件；因此根据其现状，结合沈阳市调度管理方式的经验，建立了沈阳市供水系统多目标、混合离散变量、直接优化调度模型；并根据管网的实际情况，适当放宽约束条件，以满意解为追求目标，保证了调度软件的
实用性。
　　利用本文建立的数学模型进行计算时，将原始数据输入后，经优化计算输出调度运行策略(共得五个可选方案)。经核算，所有测压点水头均满足水压要求。
　　通过计算得知，1998年3月10日利用两种方案在部分泵站所产生的直接电费分别为：优化方案38536.383元，经验方案41154.005 元。经实际比较发现，优化方案比经验方案节省电费6.36%，优化方案的运行合理性是明显的，并且其经济效益显著。

　　5 结论

　　本文在对供水系统优化调度时，针对不同的供水泵站采用了不同的寻优方法，由于定速泵可调余地小，泵站内可选择的运行策略有限，宜通过一次寻优直接求解，以保证得到可行满意解；而调速泵则通过改变水泵转速，最大限度地满足配水管网的水量水压要求，进行分级优化，简化了数学模型及求解难度，使混合离散变量直接优化模型的决策变量维数减少，提高了其计算效率，并通过二级寻优，单独对混合泵站(含调速泵泵站)进行调度决策寻优，以充分发挥调速水泵的可调能力，可使混合泵站在最优的调度策略下运行。通过对沈阳市实际供水系统进行优化调度实践（该课题已被验收），其优化效果明显。另外，由于对混合离散变量优化算法的改进，使得该优化程序的计算速度明显提高，并且在实际运行中发现，对于配水系统的各种用水情况，该优化程序经计算后，总能找到可行的满意解，一直没有出现无解的情况，可见这里提出的大规模供水系统的优化调度模型及算法是有效并且可行的。

　　参考文献：
　　［1］吕谋，张土乔，赵洪宾.供水系统的优化调度方法探讨［J］.给水排水,1998，25(12).
　　［2］赵新华，田一梅，武福平.城市配水系统优化运行的研究［J］.中国给水排水，1992，8(3).
　　［3］余俊.周济.优化方法程序库OPB-1［M］.北京：机械工业出版社，1989.
　　［4］Lindell E O,Kevin E L.Optimal control of water supply pumpingsystems［J］.Water Resources Planning and Management,1994，120(2).
　　［5］Yung?Hsin Sun.Generalized network algorithm for water?supply?system optimization［J］.Water Resources Planning and Management，1995，121(9).

---

作者简介：吕谋(1965-)，男，山东青岛人，浙江大学副教授，博士后，研究方向：给水系统优化。
电话： (0571)7996721
E-mail: [email protected]
收稿日期： 2000-04-20