给水管网设计中的一种流量分配方法
俞国平
(同济大学 环境科学与工程学院,上海 200092)
摘要:讨论了管网流量分配对给水管网优化设计结果的影响,指出带有树枝网特征的流量分配形式在环状给水管网设计中产生了较好的效果,研究了非线性最小费用网络流算法用于搜索最优流量分配树。
关键词:流量分配;优化设计;给水管网;最小费用网络流
中图分类号:TU991.32
文献标识码:C
文章编号:1000-4602(2000)04-0031-03
在城市给水管网设计中,管道的流量分配会对设计流量产生重大影响。环状给水管网由树枝管道和余枝管道组成,树枝管道构成给水管网的树枝形供水脉络,余枝管道则形成供水回路。比较好的流量分配形式是管网中所有的余枝管道都应取其需通过的最小流量值。然而在规模较大的给水管网中可以构造出上百万计的树枝网数目,其中供水最经济的树枝网称之为最优流量分配树,在此基础上分配给余枝管道以适当的最小允许流量,便产生了一种带有树枝网供水特征的环状给水管网的流量分配形式,协调供水经济和安全的矛盾,取得较好的设计效果。
1 管网优化设计的数学模型
当管径被取为设计变量时,给水管网优化设计的数学模型表达为:
![]()
约束条件:
Lh=0 Aq+Q=0
hi=k3qieli/Di3 Di≥Dmini i=1,2,...mo
通过水头损失计算公式,把设计变量管径D分解成管道流量q和管道压降h,并略去常数项,于是原模型分解成下述两个各有其意义的优化模型。
模型 1
![]()
约束条件:
Lh=0
h>0
模型2:
![]()
约束条件:
Aq+Q=0
qi≥qmini
式中 q--管道流量?
h--管道压降?
l--管道长度?
Q--节点流量?
ns--水源个数?
A--管网的衔接矩阵?
L--管网的回路矩阵?
H0--控制点所需压力标高?
Pi--控制点到第i个水源节点的某一指定方向的沿线管道集合。
b、e?--管道造价系数
α、β--水力摩阻公式中的系数
k1、k2、k3--与资金回收、电价、水泵效率等因素有关的常数
模型1表示管道流量已知条件下,对管道压降h进行优化设计以降低管道造价和运行费用之和。?
模型2表示在管道压降不变时,对管道流量q进行最优分配计算以降低管道造价。
把上述两个模型串联起来协调地求解要比直接求解以管径d为设计变量的优化模型容易得到逼近全域最优解的局部解。计算步骤如下:
① 给定初始可行流量分配q0,求解模型1得到最优压降h*;
② 保持h*不变,求解模型2得到最优流量分配;
③ 若q*=q0,计算终止,h*、q*为优化设计最优解;否则,令q*→q0,转入步骤①。
2 最优流量分配树的搜索
模型2改写为:
![]()
式中 ![]() ,是相对于第i 根管道流量的费用权重,模型2的求解就是满足节点流量平衡方程和流量界限约束的最小费用网络流,由于ea/β≠1,这是一个非线性网络流问题。
,是相对于第i 根管道流量的费用权重,模型2的求解就是满足节点流量平衡方程和流量界限约束的最小费用网络流,由于ea/β≠1,这是一个非线性网络流问题。
在管道网络中:管道被区分为树枝和余枝,集合标记分别为B和N,其相应的管道流量分别为基本变量qB和非基本变量qN,衔接矩阵也相应被分为AB和AN,节点方程表示为:
ABqB+ANqN+Q=0 (1)
qB=-AB-1ANqN-Q (2)
式(2)表示余枝流量已知时,即可求出树枝流量,独立的决策比纳凉是余枝流量qN,并且:
![]() (3)
(3)
为避免计算AB的逆阵,实际计算时引用切割组矩阵表达节点流量平衡方程:
(CB/CN)(qB/qN)+CQQ=0 (4)
以图1所示管网为例,切割组矩阵可表示为:

由于CB为一单位矩阵,所以有:
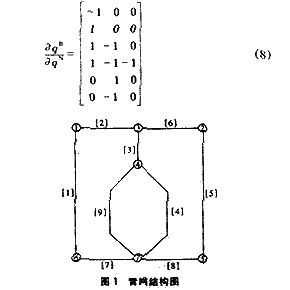
对于模型2中的目标函数,余枝流量的简约梯度可表示为:
![]()
式(9)表示余枝流量qj的单位变化所引起的目标函数的变化。由式(8)可知qi/qj?可能为1、0或-1。当初始可行流量分配确定后,计算每一回路(环)的回路校正流量Δq,即可改变流量分配方案并仍然满足流量平衡方程。
搜索最优流量分配树的最小费用网络流算法如下:
①确定初始可行的树枝和余枝的区分,其指标集分别为B和N,令qj0=qmin,j∈N,得到初始流量分配q0,0→k,k为迭代指标。
②当迭代指标为k时,qk为当前的流量分配,对所有余枝计算:

③如果对所有余枝均有Rj≥0,计算终止,qk为最优流量分配,否则令
φ=|j|Rj=max{Rj(Rj<0,j∈N)}
在第φ个回路中,令:
△q=min{(qi-qmin)}|i∈B,σi<0}
Φ={i|(qi-qmin)=△q}
④对第φ个回路中的所有管道,计算qik+1=qik+σiΔq,得到新的流量分配,在切割组矩阵中以第φ根余枝和第Ø根树枝互相交换进行转轴运算,得到新的树枝和余枝的区分集合,令k+1→k,转入②。
3 结语
本文讨论了管道流量分配方案对优化设计结果的影响,不同树枝网的流量分配产生优化后的目标函数差高达14%,而把非线性最小费用网络流算法用于寻找最小流量分配树中得到了一定成功。每根管道的最小允许流量qmin的取值应考虑管网安全供水的复核结果,目标尚无有效方法确定qmin的取值,还需继续研究。
电话:(021)65982697(O) 65981980(H)
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 [email protected] ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








