城市供水工程配水系统优化调度方法研究
路琦
【摘要】 本文以管网水力特性基本方程为基础,以节点流量为重点基本数据,阐述了包括节点流量预测、管网水力分析、工作状况核算和优化调度计算为主要内容的城市供水工程配水系统优化调度方法。
【关键词】 管网 系统 节点流量 水力平衡 核算 优化
绝大部分大中型城市的配水系统属多水源系统,若干个水厂通过城市配水管网向城市供水。城市供水系统的电耗是相当可观的,其年耗电量为全国总用电量的1%以上。生产的发展、人民生活水平的提高对供水质量(包括水质、水压)提出了更高的要求。在这种形势下,进行城市供水工程配水系统优化调度已成为国内外供水行业日益关注的问题,其目的在于:通过管网中各节点流量的逐时预测、管网水力平衡计算、管网实际工作状况的逐时核算、各节点用水量的数据修正等手段,摸清当前的城市用水状况,进而通过优化计算等手段,确定本时段各水厂供水量和供水压力的最佳组合,使得所采用的供水方案,在保证用户用水要求的前提下,能最大限度地减少电耗、降低成本。
1 对城市配水管网系统的分析
城市配水系统优化调度的研究对象是整个配水系统,无论采用什么具体方法进行配水系统优化调度,都必须是建立在给水工程专业知识和对配水系统特性深入研究的基础上。因而,对城市配水管网系统进行分析是非常必要的。
1.1 城市配水管网的水力特性和基本方程
城市配水管网是一个大型的网络系统。根据图论的基本原理,配水管网的几何图形可以抽象地认为是由节点和管段构成的有向图。若干管段顺序连接构成管线,起点和终点相互重叠的管线构成环,当一个环中不包含其它环时称为基环。节点数N、管段数M和基环数L之间的关系为:M=N+L-1。
管网的水力特性可概括地用以下两个方程组表示:
N个节点流量平衡方程:Σ±qij+Qi=0 (1)
L个基环平衡方程;Σhij=0,即ΣSijQ↑2ij=0 (2)
式中:Hi、Hj——管段两端节点i、j的水压高程
hij——管段水头损失
Sij——管段的摩阻系数
Qi——节点流量
qij——管段流量
将方程组(2)代入方程组(1),得到一组只含变量H1,H2……,Hn的方程:
Σ±[(Hi-Hj)/Sij]0.5+Qi=0令Fi=Σ±[(Hi—Hj)/Sij]0.5+Qi=0则管网水力特性基本方程组可表示为:
F1(H1,H2……,Hn)=0
F2(H1,H2……,Hn)=0
… … … … …
Fn(H1,H2……,Hn)=0
这个方程组是进行所有与配水管网有关的优化计算所必须遵从的最基本的方程组,在以后的论述中将会被多次用到。
1.2 基本数据
对一个城市的现状配水系统而言,进行任何与配水管网有关的计算时,所需的基本数据包括:各管段的管长、管径、粗糙系数和各节点的节点流量。
上述基本数据中,管长、管径是比较容易准确确定的;粗糙系数因管材的不同而异,且随使用年限的增加会有所变化,但如选择若干有代表性的管段通过测压测流对粗糙系数进行计算,粗糙系数也是可以给定得比较准确的。可以认为:管长、管径、粗糙系统是可以比较准确地确定的,且这些数据在一段较长的时间内是基本不变的,即使随着时间的推移会有所变化(如管壁积垢引起管径缩小、粗糙系数增大),其变化过程也是缓慢的。
节点流量则不同,它们变化的随机性强,而且是逐时逐刻不断变化,且变幅可能较大。
通过上述分析,假设各管段的管长、管径、粗糙系数是准确的,管网方程所采用的计算公式也是准确的、管网的计算图形准确地反映了管网的实际情况,则我们可以认为:为进行优化调度而进行配水管网水力平衡计算时,产生计算不准确的原因是由节点流量的不准确造成的。
2 城市配水系统优化调度的基本构想
根据对管网系统和基本数据的分析,确定城市配水系统优化调度的基本过程如下:
(1) 进行管网中各节点的节点流量和总用水量的逐时预测。
(2) 将预测时段的总用水量与实际发生的总供水量进行比较,将不平衡水量按一定的方法分配到各节点流量的预测值中。进行管网水力平衡计算(通过计算机程序),从而得到一组节点压力的计算值。
(3) 将计算得到的节点压力与测压点处的实测节点压力进行比较,得到一组测压点处计算压力与实测压力的压差(由节点流量的不准确造成)。进行配水管网实际工作状况核算(通过计算机计算,调整各节点流量值),使压差消失或下降到允许限度以内,以确定本时段配水管网的实际工作状况(各节点的实际用水量)。
(4) 根据调整后的本时段各节点的节点流量,进行优化调度计算,确定本时段各水厂配水量和配水压力的优化组合。
3 城市供水工程配水系统优化调度方法研究
上面我们将城市供水工程配水系统优化调度分解为四个步骤,这四个步骤可以概括为解决以下四个问题:
3.1 各节点流量的逐时预测
各节点流量的逐时预测是一项重要的工作。准确的预测可以提高管网水力平衡计算的准确性,减少计算时间,为进行实时优化调度创造良好的条件。
国内外学者曾对城市供水系统的水量预测进行过研究。Fallsicle,F.,Peny对城市总用水量的逐时预测进行研究,采用三角级数对时用水量曲线进行拟合,考虑了气候、温度的影响,通过增加状态向量的维数提高预测的精度。Hoshashi Kamei提出了采用卡尔曼滤波(Kalman Filter)进行水量预测的方法。国内的刘遂庆、陈跃春提出了对原始数据分项处理,通过建立数学模型进行水量预测的方法。
一个城市的用水量由于受季节、气候、工业生产状况、居住条件、作息时间、节假日等因素的影响,是每时每刻都在变化的。而构成城市总用水量的各节点流量,其变化的随机性更大。在我国,由于近年来经济迅猛发展,生产和生活用水量增长很快,而且这种增长可能是超常规的。这给本来就复杂的用水量预测工作增加了难度。
用水量变化的随机性,要求水量预测模型应是一个建立在概率统计基础上的数学模型。目前,国内外对用水量预测的研究还处于探索阶段,理论性大于实用性,研究重点侧重于城市总用水量的预测。
而优化调度所要求的水量预测,是管网中每个节点的逐时节点流量预测。一般来讲,节点流量变化的随机性要比城市总用水量变化的随机性大,而且每个节点流量的变化规律是不同的。大中城市的配水管网一般有几百甚至上千个节点,给每个节点建立一个节点流量逐时预测的数学模型是非常困难的,其建模工作量和计算量都是非常大的。而且,在使用过程中,要根据最新发生的情况,不断对各节点流量预测数学模型中的参数进行修正。所以,目前建立在概率统计基础上的用水量预测数学模型的研究离实用还有较大距离。
为进行城市配水系统的优化调度,目前阶段节点流量预测的一个可行的方法是:加强以往年份中不同季节、不同气候条件下一天之中不同时段实际发生的节点流量的数据统计,存入计算机数据库中,加强新用水户用水申报的管理;进行管网实际工作状况的核算,摸清当前时段实际发生的节点流量;根据当地的具体情况,辅以适当的计算方法,对下一时段的节点流量进行预测。
3.2 配水管网水力平衡计算
由水量预测我们得到将来某一时刻管网中各节点流量的预测值Qi=(i=1,2,…,n)。当这一预测时段到来时,通过各水厂出水流量计传来的数据,可以得知这一时段的城市实际用水量。由于用水量的随机性和预测的误差,预测水量和实际水量肯定不完全一致,需将它们的差值分摊到各节点流量上,然后进行配水管网水力平衡计算。
通过管网水力平衡计算,我们得到一组这一时段的管网压力计算值Hi(i=1,2,…,n);通过分布在管网中的若干个测压点,得到一组这一时段节点压力的实测值Hk(i=1,2,…,nn)。由于各节点流量预测的不准确,测压点处节点压力的计算值与实测值肯定不一致或者说存在一组压差。
在此,管网水力平衡计算的目的是:通过计算得到一组节点压力的计算值,与各测压点实测压力比较,将节点流量预测的不准确程度以测压点压力的计算与实测值的差值的形式表示出来。
管网水力平衡计算的方法是求解管网方程组:
F1(H1,H2,…,Hn)=0
F2(H1,H2,…,Hn)=0
…… …… ……
Fn(H1,H2,…,Hn)=0
采用迭代法,将方程组转换成以下形式:

本人曾就上述方程组的解法进行过一些研究。根据以上方程组,采用求节点校正压力的方法,编制了管网水力平衡计算的计算机计算程序GSNW2,并用此程序对深圳、湛江、海口、驻马店、芜湖、安庆、廊房等城市的配水管网进行过计算。由于篇幅所限,管网水力平衡计算的具体方法就不在此鳌述了。
3.3 配水管网实际工作状况的核算
通过配水管网水力平衡计算,我们得到了一组根据预测的点节流量计算的节点压力Hi(i=1,2,…n);由分布在管网中的若干个测压点,得到一组节点压力的实测值Hk(K=1,2,…,nn)。测压点处压力的计算值和实测值的差值|Hk-H↑0k|(K=1,2,…,nn)是由于节点流量预测值的不准确造成的。为了给本时段的优化调度提供准确的管网工作状况(在此主要是节点用水量),同时也为给下一时段乃至日后的节点流量预测提供准确的参考数据,需进行配水管网实际工作状况的核算。在满足管网水力平衡的条件下,调整各节点的节点流量,通过最优化计算和非线性规划等数学方法编制计算机程序进行计算,使测压点处的压差|Hk-Hk0|(K=1,2,…,nn)消失或下降到允许的限度以内,并得到一组新的、反映本时段实际情况的节点流量Qi(i=1,2,…,n)。
国内学者曾对配水管网实际工作状况的核算的计算方法进行过研究。
杨钦教授率先提出了灵敏度分析的计算方法:根据管网水力平衡方程组F(H)=0,求出各测压点处调整节点流量的灵敏度系数eHi/eQj,对灵敏度系数值最大的节点的节点流量进和调整,从而使本测压点处的压差迅速而最有效地消失。但这种方法每次只能对一个测压点处的压差进行调整,虽然这个点的压差下降很快,但其它测压点处的压差有可能增加。
韩德宏提出了配水管网实际工作状况核算的数学模型:

式中 ωj——加权因子,表示节点j的重要程度
Hk——节点K的节点压力计算值
Hk0——节点K的节点压力实测量值
Qi——节点i的节点流量预测值
Qin——节点i的节点流量调整下限
Qim——节点j的节点流量调整上限
QT——总用水量
n——节点个数
nn——测压点个数
此数学模型的意义在于:在满足管网水力平衡的条件下,通过在一定范围内调整节点流量,使测压点处的压差下降。
本人认为,无论采用什么方法来消除测压点处的压差,都应使被调整值尽可能符合实际情况为前提。节点流量的预测值虽有误差,但毕竟是根据以往年份的相同季节、相似气候、相同时刻的统计数据、变化趋势和前一时刻实际发生的数据,通过适当的计算得来的,也有准确性的一面。
基于上述分析,在此提出以下配水管网实际工作状况核算的数学模型:
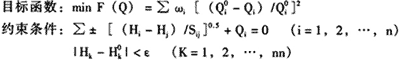
式中 ω1——加权因子,表示节点j的重要程度
Qi0——节点i的节点流量预测值
Qi——节点i的节点流量的当前值
Hi、Hj——管段两端点i、j的节点压力
Sij——管段的摩擦系数
Hk——节点K的节点压力计算值
HK0——节点K的节点压力实测值
n——节点个数
nn——测压点个数
本数学模型的意义在于:在保证水力平衡的条件下,在各节点流量的预测值调整尽可能少的情况下,使测压点处的压差下降到允许限度以内。
上面给出了三种配水管网实际工作状况核算的计算方法和数学模型。至于采用哪种方法和数学模型编制计算机程序,应结合当地的具体情况和计算机硬件的配置而定。编制程序时应尽量减少计算过程所占用的计算机内存,提高计算速度,以适应实时优化调度的要求。
3.4 优化调度
近年来,在给水工程技术发展的基础上,采用最优化技术原理,利用计算机进行城市配水系统优化调度已成为供水行业日益关心的研究课题。
优化调度的目的是确定每一时段各水厂配水量和配水压力的最佳组合。由于各地的情况千差万别,优化调度计算数学模型的目标函数也不尽相同。在目前所见资料中,优化调度数学模型所追求的目标归纳起来有以下几种:
·“配水电耗最少”
·“供水成本最低”
·“等压供水”
国内的研究多数是以“配水电耗最少”为目标,通过建立适当的数学模型,利用计算机进行优化调度计算,使计算得到的各水厂配水量和配水压力组合在整体上电耗最低。上述研究均采用十分严密的数学方法,并取得了一些阶段性的成果。但是,配水系统是一个由多台配水泵和配水管网组成的复杂而庞大的系统,经优化调度计算所得到的某台水泵的工况点(Q,H)极有可能不在水泵的Q~H曲线上而无法实施。虽然调速设备的采用为这一问题的解决带来了良好的前景,但除此之外我们还会面临其它一些问题,其中之一是:目前水泵的效率η与Q和H的关系尚难用一个数学公式准确的表示,目前所见的研究成果尚未提出一个可行的令人满意的解决办法,一般是以一个固定的效率η代替,这势必对优化调度计算结果的准确性带来很大影响。上述有待解决的问题决定了目前的研究成果还难以用到实际工程中。
另外,本人认为以“配水电耗最少”为优化调度计算数学模型的目标函数在很多情况下是不够合理的,还应考虑当地的水资源情况,输水电耗和各水厂的净水成本等因素,如果是地下水和地面水混合使用,还应考虑哪个水源优先及环境影响等。
所以,要实现真正意义上的优化调度,还有一些的理论工作和实际工作有待去完成。
在上述问题得到解决以前,实际可行的方案是相对优化。对于个城市而言,各水厂的设计供水能力、配水泵机组的台数、各配水泵机组的特性都是确定的,各水厂在不同生产负荷下的净水成本是可以预先计算得到的。在日常的工作中,可根据对将来若干时段各节点流量的预测值,通过进行管网水力平衡计算,预先为每个时段制定几套可行的配水方案,从中选择一个最优的方案做为这一时段的配水预测方案。当预测时段到来时,利用前面章节所述的管网水力平衡计算和管网实际工作状况核算等计算手段,对预测的配水方案中个别水厂的配水量和配水压力做适当的调整后,即可做为指导这个时段城市配水系统工作的配水方案并付诸实施。
应当指出,调速设备的普遍采用将为上述“相对优化调度方法”的实际运用带来了很大方便。
结束语
城市配水系统的优化调度是一个集给水工程技术、最优化计算方法、计算机技术、通讯技术、计算机编程技巧等于一体的系统工程。经多年努力,国内外研究人员已取得了卓有成效的研究成果。虽然还有不少有待进一步研究和解决的问题,但实现城市配水系统的优化调度是供水行业的发展趋势,这一课题的研究已成为国内外同行普遍关注的问题。优化调度对提高城市供水质量、减少盲目性、节约电耗和降低成本有着重大意义,前景是十分光明的。
参考文献
[1]刘遂庆,《多水源配水系统电子计算机优化调度的研究》,同济大学研究生论文,1981
[2]陈跃春,《城市配水系统的微型电子计算机优化调度》,同济大学研究生论文,1985
[3]韩德宏,《城市输配水系统的优化调度》,湖南大学研究生论文,1985
[4]杨钦,《给水管网现状的核算》,同济大学,1979
[5]Fillsicle,F.,Peny,《On line Predication of Consumption for Water Supply Network Con-trol》,1979
[6]邓晓刚,《卡尔曼滤波在城市供水系统水量预报中的应用》,同济大学研究生论文,1988
[7]严煦世、赵洪宾,《给水管网理论和计算》,中国建筑工业出版社
[8]杨饮,《管网的图论模型》,同济大学,1978
[9]俞国平,《给水管网扩建工程的最优化设计》,同济大学研究生论文,1985
[10]单方宜,《北京供水工程自来水公司供水调度管理系统(WDSS)设计经验介绍》,1996年
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 [email protected] ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








