用表面络合理论解释水溶液中离子交换行为
| 论文类型 | 技术与工程 | 发表日期 | 1999-01-01 |
| 来源 | 《中国给水排水》1999年第1期 | ||
| 作者 | 赵璇,吴天宝,云桂春 | ||
| 摘要 | 赵 璇 吴天宝 云桂春 (清华大学核能技术设计研究院) 离子交换在水处理中应用十分普遍,其理论也已经逐步走向成熟。近年来,随着工程践的深入,对离子交换理论提出了一些新见解。 1、传统意义上的离子交换理论 在传统的离子交换反应中,最简单明了的平衡理论是唐南(D ... | ||
赵 璇 吴天宝 云桂春
(清华大学核能技术设计研究院)
离子交换在水处理中应用十分普遍,其理论也已经逐步走向成熟。近年来,随着工程践的深入,对离子交换理论提出了一些新见解。
1、传统意义上的离子交换理论
在传统的离子交换反应中,最简单明了的平衡理论是唐南(Donnan)膜平衡理论[1],即对于树脂RA和溶液中的溶质AY平衡,认为阳离子A在树脂中浓度比在溶液中大得多,起初A从树脂相进入溶液相,Y从溶液相进入树脂相,致使溶液相带正电荷,树脂相带负电荷,从而在两相间形成电位差,即唐南电势,它可以表示为活度、溶胀压力和摩尔浓度对体积的偏微分函数。当浓度差所产生的作用与唐南势的作用相抵消时,即达到平衡。在离子交换中,对A、B两种离子,当体系达到平衡时,这两种离子的唐南势必然相等,由此建立等式得到选择性系数表达式。溶胀压力越大,以及两种互相交换的外来离子的摩尔浓度对体积的偏微分之差越大,则选择性系数越大。
此外,按照异相化学反应研究离子交换平衡,按照离子在两相间的分配研究离子交换平衡以及盖恩斯-托马斯的抽象热力学理论也是常用的交换理论。
以上几种理论,只是从物理化学的角度阐述了离子交换的行为,并未从微观化学反应的角度进行描述,不易理解,公式推导及结果也比较复杂,同时单纯根据热力学定律得出的结果有时并不能与工程实际相符。本文介绍用表面络合的概念来描述离子交换行为。
2、表面络合理论
主要适用于弱酸或弱碱性离子交换树脂及其它一些固相萃取剂与水溶液中离子间相互作用,德国的Hoell博士认为,水溶液中的离子之所以被树脂吸附,是因为离子与树脂表面发生了络合反应,为了描述离子交换平衡,对树脂表面作了许多假设(见图1)。认为树脂相存在一个假想的表面,官能团整齐地排列在这个表面上;树脂表面的官能团通过解离或吸收质子而使表面带电,这些电荷由被吸附的水合外来离子中和,从而形成双电层;每一种外来离子形成自己单独的排列层,该层到表面的距离为一个受离子本身因素如离子大小、电荷制约的特征值;特征距离越小,说明该离子的优先选择性越强;只有排列层的外来离子才有可能与树脂中的官能团形成络合物;官能团的电荷一部分被位于排列层的外来离子中和,一部分被位于扩散层中的外来离子中和;树脂表面与排列层形成具有一定容量的电容,层与层之间无排斥现象;每一个排列层都拥有与树脂表面相同的表面积并与其平行;电位梯度与表面垂直,由表面逐渐降低,直到排列层达到一个固定值,然后向扩散层进一步降低,直至溶液。
根据Boltzman关系,排列层中A+与溶液中A+浓度存在以下关系:
C(A)st=C(A)L·exp(-Z(A)·F·Ψst/RT) (1)
式中 C(A)——浓度
Ψ——电位
Z(A)——外来离子的价态
R——气体常数
F——法拉第常数
T——热力学温度
式(1)中下标st表示排列层,L表示液相(以下各式相同)。
2.1 二元平衡
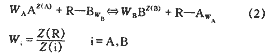
式中?R--树脂相
A、B--外来离子
Z(i)--外来离子的价态
Z(R)--Z(A)和Z(B)的最小公倍数
假定外来离子A距表面的特征距离小于B,一部分A和B位于扩散层,模型见图1。
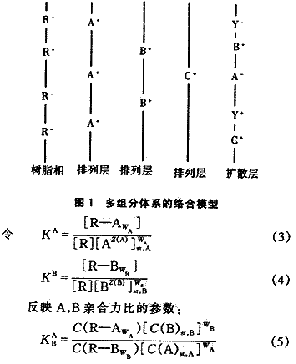
式中 C(i)--浓度
C(R-i)--排列层中形成络合物的离子浓度
C(i)st--排列层中未形成络合物的外来离子浓度
根据电容原理,树脂表面电量密度σs可由表面电位Ψs和Ψst,A及由表面与第一层排列层的电容C(S,A)?
σs=C(S,A)(Ψs-Ψst,A) (6)
σst,A=C(S,A)(Ψs-Ψst,A)+C(A,B)(Ψst,A-Ψst,B) (7)
式中 C(A,B)——排列层A、B之间的电容
σst,i——i(i=A,B)排列层的电量密度
σD——扩散层的电量密度
下标s表示树脂相表面,D表示扩散层(以下各式同)。?
由电荷平衡:
σs+σst,A+σst,B+σD=0 (8)
表面的电量密度σs为官能团与扩散层中外来离子数目的总和,A、B两个排列层的电量分别等于层中外来离子A、B所带电量。
σs=-FLs[Z(R)C(R-AWA)-Z(A)C(A)st,A+Z(R)C(R-BWB)-Z(B)C(B)st,B-σD]/A0S (9)
σst,A=-FLs[Z(R)C(R-AWA)-Z(A)C(A)st,A]/A0S (10)
σst,B=-FLs[Z(R)C(R-AWB)-Z(B)C(B)st,B]/A0S (11)
式中 Fls/(A0S)---把摩尔浓度转化为电量密度
L --液体体积?
Ls--靠近树脂表面的液体体积?
A0--比表面积?
S--树脂质量
2.2 多组分平衡?
假设有N种外来离子被吸附,假定排列层的排列顺序如下:S/A/···/I/J/···/N/D/。可以认为每种离子达到各自的局部平衡,并有着各自单独的络合物形成常数。N种外来离子形成N个排列层,每一层与表面之间形成电容器并拥有电容C(S,I)。另外,两个相〖CM(22〗邻的外来离子之间形成N-1个电容,电容值为C(I,J)。
由电中性原则可以得:
![]()
电量、电容和电压存在以下关系:
σs=C(S,A)(Ψs-Ψst,A) (13)
σst,A=C(S,B)(Ψst,A-Ψs)+C(A,B)(Ψst,A-Ψst,B) (14)
σst,I=C(S,I)(Ψst,I-Ψst,I-1)+C(I,J)(Ψst,I-Ψst,J) (15)
σst,N=C(S,N)(ΨN-ΨN-1)+CD(ΨN-ΨD) (16)
σD=CD(ΨD-ΨN) (17)
对于每一层存在电量平衡关系:

2.3 二元体系中的分离因子
利用?Boltzman?关系可以得到两种外来离子络合常数的比值:

排列层中未络合与络合的外来离子以及扩散层中的外来离子的总和构成树脂负荷,如果浓度用mol/L、负荷q用当量/克树脂表示,则可以得到:?
Z(R)C(R-AWA)-Z(A)C(A)st,A-Z(A)C(A)D=q(A)S/Ls (23)
Z(R)C(R-AWB)-Z(B)C(B)st,B-Z(B)C(B)D=q(B)S/Ls (24)
由式(6)、(7)、(8)、(11)可以得出:
Ψst,A-Ψst,B=FLs[Z(B)C(B)st,B-Z(R)C(RBWB)]/A0SC(A,B) (25)
相对于排列层而言,扩散层中的电量很小,排列层中未络合的离子又远远小于发生络合的离子的量,因此这两部分离子的量可以忽略。根据式(24)可以得出式(25)括号内为:
Z(B)C(B)st,B-Z(R)C(R-BWB)=C(B)=y(B)qmaxS/Ls (26)
式中 qmax——树脂的总容量
y(B)——B离子在树脂相内的当量百分比
则 ![]()
在忽略扩散层中外来离子的前提下,分离因子的对数值与外来离子的无量纲负荷呈直线关系,由此而确定的![]() 充分体现了液相总浓度和树脂相的组成。
充分体现了液相总浓度和树脂相的组成。
根据络合理论,![]() 随着y(B)增长的速度与A,B两个排列层间的距离成比例。随着两个排列层间的距离增大,电容器的电容增大,直线的斜率也增加;相反,如果两种外来离子处于同一层中,电容值为无穷大,斜率为零,此时
随着y(B)增长的速度与A,B两个排列层间的距离成比例。随着两个排列层间的距离增大,电容器的电容增大,直线的斜率也增加;相反,如果两种外来离子处于同一层中,电容值为无穷大,斜率为零,此时![]() 为恒定值,亲合力
为恒定值,亲合力![]() 与斜率可以从实验中通过作
与斜率可以从实验中通过作![]() —y(B)的曲线获得。
—y(B)的曲线获得。
2.4 多组分体系中的分离因子?
假定排列层的排列顺序如下:S/A/…/I/J/…/N/D/。因此存在N-1个下式:
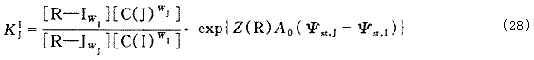 ?
?
上式的前半部分即为多组分体系中任意平衡I/J的分离因子,不考虑扩散层,则:
![]()
式中?K--从J到N的外来离子
分离因子的对数值可以由相似于二元体系中近似方法得到:
![]()
3 验证实验
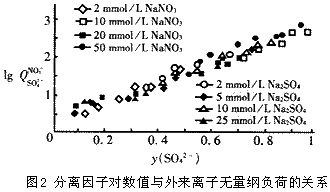
利用阴离子交换树脂进行实验室规模的试验,对以上得出的结论,即对分离因子的对数值与外来离子的无量纲负荷呈线性关系进行检验。结果如图2。在实验中,分别以硫酸根离子(树脂为硝酸根型)与硝酸根离子(树脂为硫酸根型)做外来离子,可以看出,分离因子的对数值lgQ与y(I)呈线性关系,并且该直线与外来离子的初始浓度无关。另外,用阳离子交换树脂做类似实验,也得到相同结果。
4、评述
该模型是目前国内外仅有的以络合理论来解释离子交换树脂对离子吸附行为的模型,认为离子之所以被树脂吸附,是因为处于排列层中的离子与树脂表面发生络合反应。与传统理论相比较,模型本身比较简单,直观,易于理解。得出分离因子的对数值与外来离子的无量纲负荷呈线性关系的结果,一方面计算比较简单,另一方面与试验结果符合较好,能够用来指导试验。表面络合理论由于其直观的模型、简单的结果、以及对实际较好的描述而显示出其优越性。
但是,该模型的目的仍然是解释离子交换行为的模型,本质上是一个交换模型,即用各种重金属离子所处的排列层距树脂表面的距离来表征选择性大小,远距离的被近距离的所取代。该模型假设太多、理想化程度较高,树脂的内部传质,树脂与溶液之间传质都未曾考虑,树脂官能团的表面化假设也忽略了树脂的内部传质。因此该模型在应用于描述比较复杂的水质(例如阴离子、阳离子和有机物的体系)的离子交换行为尚有待于进一步改进和完善,一般用于弱碱性或弱酸性离子交换树脂对离子吸附行为的描述。
此外,在最近发展起来的以表面络合理论为基础,利用阴离子交换树脂去除饮用水中痕量重金属污染的新型工艺中,该模型显示出其巨大的优越性。
参考文献
1、陶祖贻,赵爱民. 离子交换平衡及动力学. 西安:原子能出版社,1989.34~51?
2、Hoell W H,Franzreb M,Horst J et al. Description of ion exchange equilibria by means of the surface complexation theory. In:Marinsky J A,Marcus Y,ed. Ion Exchange and Solvent Extraction,A Series of Advances:Vol.11.Marcel Dekker,New York,NY,1993
3、Horst J,Hoell W H,Eberle S H. Application of thesurface complex formation model to exchange equilibria on ionexchange resins. Reactive Polymers,1990;13:209~231?
作者通讯处:100084 清华大学核能技术设计院?
(来稿日期 1998-09-10)
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 [email protected] ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








