管网生活给水设计流量的通用概率公式①
出 自: 《中国给水排水》 1995年第5期第32页
发表时间: : 1995-5
哈尔滨建筑大学张景成周利刘晓阳;崔福义(哈尔滨建筑大学);孙晓旭(黑龙江省纺织工业设计院)
进行给水管网设计时,最为困难的部分是生活给水设计流量的计算,因为生活用水量具有随机性很大而难于确定的特点。目前我国生活给水设计流量的计算方法是依室内给水和城市给水两类管网,分别以不同的公式计算(参见给水排水设计手册),介于二者之间的居住小区给水管网尚无合适的流量计算公式。从概率理论出发,建立适用于各种规模管网的生活给水流量通用计算公式,解决小区给水流量计算问题是本文拟讨论的。
1 生活给水设计流量概率公式的建立
居民生活用水量具有随机性,可将概率理论用于确定管网设计流量。设某管网供给n户居民生活用水,每户的用水方式以流量D(L/s)用水或流量为零,任一时刻用水的概率为p,各户用水情况彼此独立。则该n户居民的总用水量在0~nD(L/s)之间变化。在一给定时刻,n户民民中有i户同时用水的概率为P,i是一个随机变量以x表示。国内外的研究都认为此概率遵循二项分布:
P(x=i)=( ![]() )·p i ·(1-p) n-i (1)
)·p i ·(1-p) n-i (1)
设至多有m户同时用水的概率为P m ,则
P m =P(x=1)+P(x=2)+……+P(x=m)
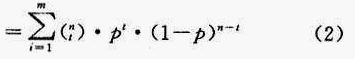
在概率P m 下n户居民最大用水量为
Q n =D·m (3)
此即生活给水设计流量的基本概率计算式。P m 代表给水保证率,由设计管网对给水可靠性的要求决定。二项分布在实际应用上很不方便。根据概率理论在户数n较大时,可构造变量y以简化为正态分布:
![]()
np为在p概率下同时用水户数估计值的下限。y仍为随机变量,符合标准正态分布。|y|不超过某一定值r的概率为:

r值的选取反映了一定的供水保证率。在此y>0,则满足概率(保证率)为 ![]() 。例若取r=1.8,保证率为99.5%,实际用水量超过式(3)计算流量的概率只有0.5%。
。例若取r=1.8,保证率为99.5%,实际用水量超过式(3)计算流量的概率只有0.5%。
当n较大时(n>100),以式(1)、(5)为代表的两种概率分布结果十分接近,设计流量相差不超过5%。所以一般情况下可以以形式较简洁的正态分布计算式为基础,导出实用的设计流量公式。设一户在一天24h内用水机会均等,最高日用水量为d,有p=d/D;令h=m-np=r

式(6)与实际情况还会有一定差距,包括:①规定用水方式为一户居民以流量d用水或以流量为零的假设过于极端,若D为一户最大用水量则实际用水量在0~D之间分布;②实际用水并非24h概率相等,有一些时间用水概率较高;③在n较小时精度较低。对上述情况进行修正,引入修正系数K ∞ 及T,可得新的计算式:

其中K=D/d,在一定的用水条件下可以导出具体的计算公式。例如,按平均每户3.5人,最高日用水量为250L/人计,约有d=864L/d=0.01L/s;用水情况最多时为2个水龙头同时开,D=0.5L/s;并取K ∞ =1.8,T=34.5,r=1.5(相应的保证率为98.3%),有:
![]()
式(7)、(8)就是管网生活给水设计流量的实用概率公式。
2 对概率流量计算公式的讨论
2.1 概率流量计算公式的适用范围
从上述推导过程中可以发现,该流量计算公式是以概率理论为基础,并对实际用水情况作了若干简化假设和若干修正,式(7)、(8)实际上是半理论半经验的公式。在概率计算公式的推导过程中并未对管网的形式加以限定,因此可以解决包括小区给水管网在内的各种管网的生活给水流量计算问题,这已被国外的类似研究所证实。但具体参数的取值同家庭结构、用水标准、用水习惯等因素有关,还应进一步研究。
2.2 与室内给水流量计算公式的比较
式(8)的形式同我国现行规范室内生活给水设计秒流量式相近,只是后者以给水当量数为变量,并缺少常数项。在进行室内给水管网设计时,以用水卫生器具当量数为变量有使用方便的特点,也适合我国传统上住宅卫生设施比较规范单一、用水人数(或户数)与卫生器具当量数之间关系较为稳定的状况。但近年住宅建设呈多样化趋热,用水人数与卫生器具当量数之间的关系也日益复杂化。然而决定生活用水流量的根本因素是用水人数及其用水标准,所以以人数或户数(人数=户数×平均人数/户)为变量建立类似式(7)、(8)形式的设计流量公式是合理的。
2.3 与最大时流量公式的比较
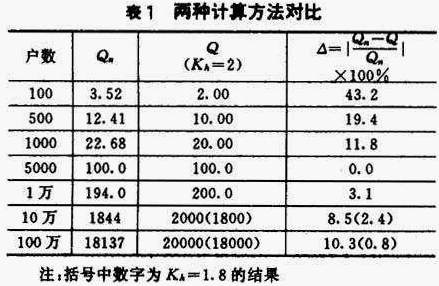
在研究住宅小区生活给水流量计算方法问题时,有人将室内给水设计流量计算式同城市给水设计流量计算式相比较,并以取二者中较大值为设计值的原则进行选取。这种方法未从根本上分析两种计算公式的适用性,取偏大值作为设计值是安全的但未必是合理的。在按最大时法进行流量计算时容易忽视时变化系数K h 的取值,一些研究都将K h 视作常数(例如取K h =2),事实上K h 是随管网服务人数多少而变化的,设计用水人数越少K h 越大,反之人口数越多K h 越小,并趋向于常数。一般计算城市管网时K h 可取定值,但规模较小的管网随服务人口数的增减而导致用水均匀性有较大变化,K h 再作为常数对待就会产生较大误差,现将式(8)与城市给水流量计算式比较以说明。根据推导式(8)的用水条件,取用水量标准每户为864L/d,则城市给水流量最大时公式可表示为
Q=0.01nK h
n代表户数。计算结果列于表1。
表1证明,当取K h =2不变时,Q n 与Q的数值在n=5000户时相同;在n较大或较小时Q n 与Q之间有一定偏差,但随户数增减适当调整K h 值,则两种计算方法显示出高度的一致性,例如户数达10~100万相差仅为2.4~0.8%,当户数减少时也可得出类似的结果。当然,户数较多随用水人数增多,用水均匀性增强,在最大时内用水量的变化减弱以至不明显,则式(8)的设计秒流量就与城市给水最大时平均流量趋向相等。由此可认为城市给水最大时流量法是式(8)的一种简化形式,二者数值的差别只是取值计算误差。在用水人数较少时,K h 变化较大而难以确定,且1小时内用水量的变化也较大必须考虑,应采用式(8)形式计算设计流量,这是室内给水管网的情况;在用水人数较多时K h 变化不大较好确定,最大时内流量的变化较小可忽略,按最大时流量法计算较为方便,这是城市给水管网的情况。在管网规模介于二者之间时(例如小区管网),K h 不太明确,以采用概率式(8)较可靠。
2.4 对时变化系数K h 的修正
更进一步,可将时变化系数K h 加以修正,以流量变化系数K n 代替。因为Q n 代表在一定概率下的最大用水量,(nd)代表最高日平均时流量,所以令K n =Q n /nd,则由式(7)有:
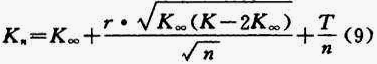
或在式(8)的用水条件下有:
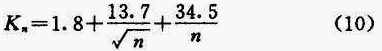
K n 是同用水户数(或人口数)有关的系数,随n增加而减小。引入K n 后,管网的设计流量就可由下式计算:
![]() (11)式中N为用水户数,q为用水量标准。虽然式(11)的形式与最大时流量公式一致,但K n 与K h 的内涵完全不同,两种计算公式有不同的适用范围。应用式(11)时无需再对管网规模加以区别,无论是城市给水、室内给水还是小区给水管网,都可采用该简单而统一的公式进行流量计算。
(11)式中N为用水户数,q为用水量标准。虽然式(11)的形式与最大时流量公式一致,但K n 与K h 的内涵完全不同,两种计算公式有不同的适用范围。应用式(11)时无需再对管网规模加以区别,无论是城市给水、室内给水还是小区给水管网,都可采用该简单而统一的公式进行流量计算。
3 参考文献
1.《数学手册》编写组,《数学手册》,高等教育出版社,1979年第1版。
2.易新琼,“小区给水流量计算的探讨”,《建筑给水排水新技术》,湖南大学出版社,1989年第1版。
3. J.TRIBUT,Determination du dedit de pointe, Science et Techniques Municipales, Octobre 1969.
① 本文承蒙李圭白教授审阅并提出宝贵意见,谨致谢意。
作者通讯处:150006 哈尔滨建筑大学435信箱
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 [email protected] ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








