沉淀池沉淀去除率计算和表面负荷率确定的新方法
| 论文类型 | 技术与工程 | 发表日期 | 1995-04-01 |
| 来源 | 《中国给水排水》在1995年第4期 | ||
| 作者 | 张玉先 | ||
| 关键词 | 沉淀池 表面负荷率 去除率 | ||
| 摘要 | 在水处理过程中常利用沉淀池固液分离,尽管沉淀池型式各种各样,而去除水中悬浮颗粒的基本原理相同。在沉淀池设计时,常常采用经验方法,如选用较长的沉淀时间或较低的表面负荷率等。显然,这些设计方法有可能使沉淀池相差很大。众所周知,衡量沉淀池沉淀效果的好坏,表面负荷率是一个主要指标、是沉淀池设计的重要依据,利用简便的方法确定其值可以使设计更趋合理。按照水中悬浮物性质、含量多少分类,常分为凝聚沉淀和非凝聚沉淀,分别采用等效沉淀曲线和累计分布曲线计算沉淀去除率。笔者发现这两种沉淀去除率计算方法可以统一为一种方法,大大简 | ||
出 自: 《中国给水排水》 在1995年第4期
发表时间: : 1995-4
张玉先
( 同济大学)
1 概述
在水处理过程中常利用沉淀池固液分离,尽管沉淀池型式各种各样,而去除水中悬浮颗粒的基本原理相同。在沉淀池设计时,常常采用经验方法,如选用较长的沉淀时间或较低的表面负荷率等。显然,这些设计方法有可能使沉淀池相差很大。
众所周知,衡量沉淀池沉淀效果的好坏,表面负荷率是一个主要指标、是沉淀池设计的重要依据,利用简便的方法确定其值可以使设计更趋合理。按照水中悬浮物性质、含量多少分类,常分为凝聚沉淀和非凝聚沉淀,分别采用等效沉淀曲线和累计分布曲线计算沉淀去除率。笔者发现这两种沉淀去除率计算方法可以统一为一种方法,大大简化了凝聚沉淀繁琐的计算过程。
2 凝聚、非凝聚沉淀去除率计算的统一
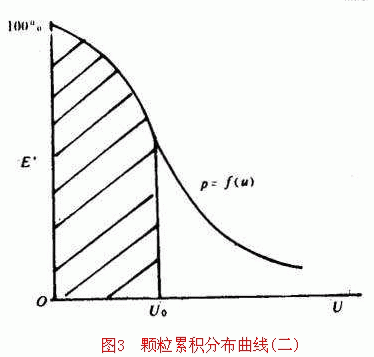
1946年,甘布(Camp)针对非凝聚沉淀过程提出了单点取样积分计算去除率方法。即从沉淀实验柱下部的取样口每隔一定时间取样一次,测定水中剩余悬浮物含量,绘出颗粒累计分布曲线(如图1所示)。当沉淀时间为t o 时,所对应的颗粒沉速为u o ,沉淀总去除率E按下式计算:
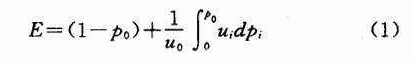
式中 p o ——沉速<u o 的颗粒占所有颗粒的重量比
u o ——沉淀颗粒的临界沉速
u i ——沉速<u o 的某一颗粒沉速
dp i ——具有沉速为u i 的颗粒占所有颗粒重量比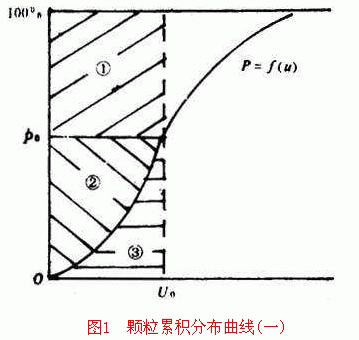
在已知沉淀池截留速度u o 时,可用图1求出总去除率。由于沉速≥u o 的颗粒去除比u i /u o =1,所以沉速≥u o 的颗粒去除率等于阴影①的面积除以u o ,其值等于1-p o 。由图1还可以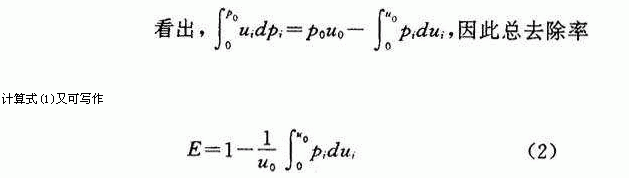 }
}
式中 p i ——沉速<u i 的颗粒占所有颗粒重量比
1958年埃肯非尔德(Eckenfelder)根据凝聚沉淀过程提出了多点取样图解配线积分计算法。即在沉淀柱上设置多个取样口,每隔一定时间取样一次,测定各水样悬浮物含量,绘出若干条等效沉淀曲线。为便于说明问题,现仅绘出两条等效沉淀曲线(见图2),于是可求出沉淀时间为t 0 时的沉淀总去除率E′,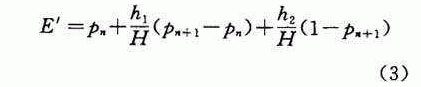
式中 p n 、p n+1 ——悬浮物去除百分数
h 1 、h 2 ——曲线间的中点高度
我国大多数教科书普遍采用了该计算方法。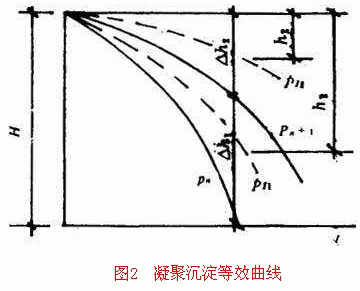
上述凝聚沉淀和非凝聚沉淀去除率计算方法实际上是一种方法的两种形式,均可采用式
(1)进行计算,证明如下:
现设两条等效曲线间距为△h,两条相邻等效曲线平均值为p I ,则有
p I1 =1/2(p n +p n+1 )
p I2 =1/2(p n+1 +1)
变化式(3)得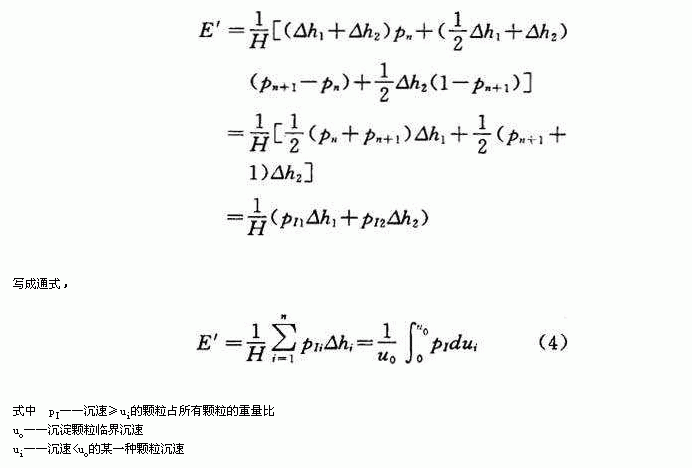
![]()
由此证明E=E′。故说明凝聚沉淀和非凝聚沉淀均可按照非凝聚沉淀计算去除率,即均可采用单点取样试验方法分析计算。在图2中,如果把等效沉降曲线首尾连成直线,完全变成了非凝聚颗粒的等效直线,总去除率计算结果不变。于是,可使凝聚沉淀试验步骤简化,计算方便,误差减小。
3 沉淀池表面负荷率的确定
沉淀池面积的大小决定于沉淀颗粒的临界沉速,也即是所选用的表面负荷率的大小。众多的研究提出了去除率与沉速、沉淀时间的关系式。Eckenfelder提出p 1 =f(h/t m ),p 2 =f(u/t n );苏联学者Ю·M费尔采提出t 1 /t 2 =(h 1 /h 2 ) k 等。很明显,这些计算方法必须求出不同沉速的去除率及m、n、k值,实际上是按多点取样试验后计算回归成p=f(h/t)的关系式,计算繁琐。如果按照沉降颗粒累计分布曲线确定临界沉速,则计算更为简便。现引入沉降颗粒经沉淀后未被去除部分占所有颗粒重量比概念——沉淀剩余率p s 进行分析。
在设计沉淀池时,已知悬浮物含量为c o ,设计要求出水悬浮物含量为c i ,则沉淀池对这种

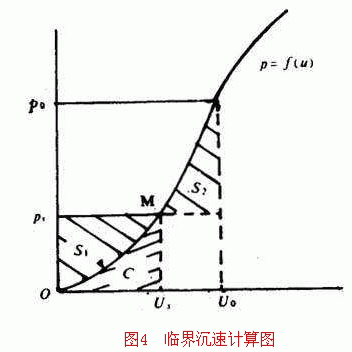
如图4所示,p o u o 等于曲线上下两块面积之和,即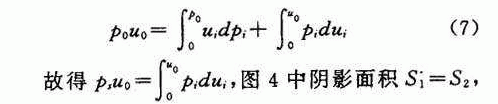
因p s 为已知,只要在累计曲线图上作图使S 2 =S 1 ,便可确定u o 和p o 值,也就确定了沉淀池的面积。
但是,这种等面积作图法并非能直观简单
在绝大多数情况下,累积分布曲线p=f(u)光滑,单调增值,且f(u)的一阶导数、二阶导数都不为零。经对多种水样沉淀试验分析,当p<50%时,其累积分布曲线都可近似回归为如下方程式:
p=Au n (9)
式中A为系数>0,n为指数,于是得: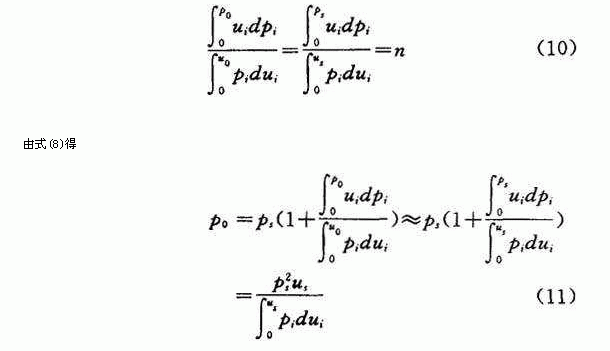
因为p s =c i /c o 为已知数,在累计分布曲线图上很容易求出u s 。这样只要在图4中求出Op s Mu s 曲线上下任一小块面积S 1 或C,勿需求出累积分布曲线方程就可确定p o 值,也就确定了u o 值。
4 沉淀池计算实例分析
沉淀池设计计算方法大致有以下几种:
① 按照沉淀时间或水平流速设计计算;
② 按照临界沉速计算式进行设计计算;
③ 按原水水质不同选定沉淀池表面负荷率设计计算;
④ 按多点取样试验求出E~u曲线确定临界沉速计算。
这四种方法中①、③方法计算多凭经验选定设计参数,②、④两种方法计算复杂。
[例]现有原水分析资料:
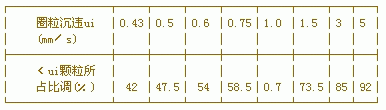
进水平均悬浮物浓度C o =430mg/L,流量4500m 3 /d,经沉淀后出水悬浮物含量C i =150mg/L,沉淀池有效水深取1.8m,试计算沉淀池面积。
① 按选定沉淀时间计算,取沉淀时间1h,则沉淀池面积为A=Q/24×1/1.8=4500/24×1/1.8=104.2m 2 ,
② 按选定临界沉速计算,临界沉速计算式为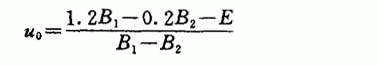
式中 B 1 ——沉速为1.2mm/s时的去除率
B 2 ——沉速为0.2mm/s时的去除率
E——设计去除率,E= ![]() =65%
=65%
经计算,B 1 =0.49,B 2 =0.85,得u o =0.64mm/s;沉淀池面积为A= ![]() 81.4m 2 。
81.4m 2 。
③ 按选定表面负荷率计算,原水悬浮物含量>250mg/L时,取表面负荷率u o =0.5mm/s,于是得沉淀池面积为A= ![]() =104.2m 2 。
=104.2m 2 。
④ 按等效沉淀曲线计算,当E=65%时求得u o =0.6mm/s,则沉淀池面积A=K ![]() =108.5m 2 ,其中K取1.25(通常K取1.25~1.75)。
=108.5m 2 ,其中K取1.25(通常K取1.25~1.75)。
结果表明,各计算方法求出的沉淀池面积不同,有的留有较大余地,有的达不到出水要求。
如果按照沉淀颗粒累积分布曲线计算,则E= ![]() =0.65沉淀剩余率p s =0.35得颗粒临界沉速u o =0.55mm/s,沉淀面积A=94m 2 。鉴于实际沉淀池受紊动作用影响,将发生进一步絮凝作用,沉淀效果一般均高于计算结果,故该沉淀池面积设计成94m 2 足以满足沉淀要求。
=0.65沉淀剩余率p s =0.35得颗粒临界沉速u o =0.55mm/s,沉淀面积A=94m 2 。鉴于实际沉淀池受紊动作用影响,将发生进一步絮凝作用,沉淀效果一般均高于计算结果,故该沉淀池面积设计成94m 2 足以满足沉淀要求。
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 [email protected] ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








