接触氧化法过滤除铁规律的数学模式的探求
| 论文类型 | 技术与工程 | 发表日期 | 1992-08-01 |
| 来源 | 《地下水除铁除锰学术论文集》 | ||
| 作者 | 刘灿生 | ||
| 摘要 | 刘 灿 生 接触氧化法过滤除铁,含铁浓度沿滤层深度逐渐下降。但其分布规律的一个重要特征是随着过滤时间的增加,滤层的除铁效能逐渐提高,含铁浓度沿滤层分布曲线相樱煜移。这种含铁浓度分布曲线上移的现象,在接触氧化法除铁中是最一般的现象,它表明接触氧化法除铁反应过程是加速反应或自动催化反应过程 ... | ||
刘 灿 生
接触氧化法过滤除铁,含铁浓度沿滤层深度逐渐下降。但其分布规律的一个重要特征是随着过滤时间的增加,滤层的除铁效能逐渐提高,含铁浓度沿滤层分布曲线相樱煜移。这种含铁浓度分布曲线上移的现象,在接触氧化法除铁中是最一般的现象,它表明接触氧化法除铁反应过程是加速反应或自动催化反应过程。含铁浓度沿滤层分布的第二个特征,是滤层不同深度处的含铁浓度对原水含铁浓度的比值,比滤层厚度在单对数标痤系上呈直线关系,这种关系经实验验证,也是接触氧化法除铁中普遍存在的。滤料粒径、滤速以及经历不同的过滤时间,虽然沿滤层分布的含铁浓度曲线发生变化,但仍然遵守上述的“直线律”。含铁浓度分布曲线的“上移律”和“直线律”在接触氧化法除铁的所有生产和模型实验中都可以看到,是接触氧化法过滤除铁滤层含铁浓度分布的主要规律。
为了描述在接触氧化法除铁过程中,亚铁离子在滤层中的去除规律,笔者依据含铁浓度沿滤层深度分布规律的两个特征(上移律,直线律)为基础,从接触氧化法过滤除铁的过程出发,建立了接触氧化法除铁的数学模型。
一、接触氧化法过滤除铁基本数学模型的建立
为了建立描述亚铁离子在滤层中去除规律的数学模型,特作如下假设:
1、滤料本体具有吸附水中亚铁离子的能力;滤料本体的作用只发生在新滤料运行初期;它作用的结果与催化作用无关。
2、滤料表面所复盖的铁质滤膜对水中亚铁离子的氧化有强烈的催化作用,截面在滤层中的铁质氢氧化物仍然是催化物质;成熟滤料表面完全被活性滤膜复盖时,其滤料本体作用不再发生。
3、成熟滤层的除铁率由亚铁离子向滤膜表面的扩散速率所控制,被吸附在滤膜表面上亚铁离子的氧化水解速度非常快,认为瞬间完成。
4、滤前水中铁质均为亚铁离子形态;水中含有充足的溶解氧;滤料粒径均匀且为球形。
关于基本假设一、二、三的结论内容,是笔者在曝气接触氧化法除铁实验研究中得出来的。它的实验验证及研究过程,拟另文论述,此处仅作为基本假设条件给出。
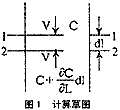
满足上述四条基本假设条件的滤层,被间距为d1的两个平行截面所截(如图1)。若令滤层的横截面积为单位面积,则截面间的微元滤层的体积在数值上等于微元长度d1,即
dv=dL
再令进入分离微元滤层的亚铁离子浓度为c,滤速为v,则流出微元滤层的亚铁离子浓度为(![]() )。若令过滤时间为dt,那么,根据质量连续关系,在dt时间内流入微元滤层的亚铁离子的数量,等于在这段时间内流出微元滤层的亚铁离子与微元滤层中截留的亚铁离子以及在微元滤层的空隙中所含的亚铁离子数量和总和,即
)。若令过滤时间为dt,那么,根据质量连续关系,在dt时间内流入微元滤层的亚铁离子的数量,等于在这段时间内流出微元滤层的亚铁离子与微元滤层中截留的亚铁离子以及在微元滤层的空隙中所含的亚铁离子数量和总和,即
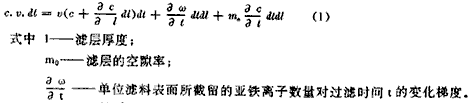
滤料层中所截留的铁质ω包括了滤料本体吸附的亚铁离子和活性滤膜去除亚铁离子数量之和:
ω=ω1+ω2 (2)
式中 ω1——由于滤料本体吸附亚铁离子,使得单位滤料表面所截留的铁质数量;
ω2——由于活性滤膜的作用,使得单位滤面所截留的铁质数量。
将式(2)代入式(1)中,并整理得
![]()
在正常过滤中,滤层空隙里的水所含的亚铁离子数量对整个滤层的除铁影响很小,因此,式(5)中右端第三项可忽略不计,于是得到
![]()
式(4)表示经过dl滤层的滤后水中亚铁离子浓度减少的速率等于截留在dl滤层中铁质增加速率。
根据基本假设1,滤料本体去除亚铁离子吸附规律,它的去除速率可用吸附传质速率来表示[4]
![]()
式中 KG——吸附传质系数;
c*——与单位体积滤料表面吸附平衡时的亚铁离子平衡浓度。
c——实际的亚铁离子浓度。
根据基本假设2、3可知,成熟滤层去除亚铁离子的过程由扩散过程所决定,因此,亚铁离子在成熟滤层中的去除速率可用扩散速率表示,而且,滤层的除铁速率随着滤层中截留的铁质增加而加快,于得得到
![]()
式中 D——界面层内亚铁离子向活性滤膜表面的扩散系数;
δ——扩散界面层厚度;
S——活性滤膜的比表面积;
ω——滤层中截留的铁质数量;
a——比例参数。
将式(6)、(5)代入方程式(4)得
![]()
式(7)是接触氧化法过滤除铁的基本微分方程。
二、基本微分方程式的求定解
在实际的接触氧化法过滤除铁中,滤料本体对亚铁离子的吸附作用是短时间的,而成熟滤料稳定除铁的接触氧化作用是经常的,是除铁的主要工作状态。因此,本文只讨论成熟滤层的除铁情况。
成熟滤层由于滤料表面已为滤膜物质所包围,滤料本体吸附亚铁离子的过程不再进行,即KG =0,因此,式(9)可化成
![]()
将式(8)对时间t求偏导数,得
![]()
经过接触滤层水中含铁量减少的速率等于滤层内铁质增加的速率:
![]()
将式(10)代入式(9)得
![]()
方程式(11)描述了在成熟滤层中亚铁离子去除的动力学过程。
当开始过滤时(t=0),滤层中未截留铁质(ω=0),式(11)可简化、积分为
C|t=0 = C0e-lDS/σu (12)
边界条件很明显,未进入滤层水的含铁浓度始终为c,即
C|l=0 = C (13)
于是,方程式(11)连同第一类边界条件的求定解问题转化为下面的数学问题:
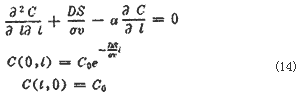
式(14)为常数双曲线型方程。
作变换
C=θeλ+ξl (15)
其中λ和ξ是待定常数。
将式(15)代入式(11)中整理得
![]()
现令
λ-a=0,则λ=a
ξ+ DS/σu=0,则ξ=- DS/σu
故在变换
C=θeat-DS/σu·l (17)
之下,方程式(16)可简化为
![]()
注意到DS/σu·a=const,则式(18)为常系数偏微分程。
令θ=θ(Z),Z=[(t-t0)(l-l0)]0.5:且代入方程式(18)中,则式(21)代为Bessel方程:
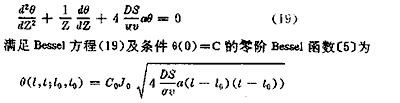
当以初始过滤(to=0),以表面滤层为基准(lo=0)为最初条件,则有
θ(l,t) = C0J0[4(DS/σv)alt] (20)
第一类零阶Bessel函数的展开式为[6]
![]()
于是
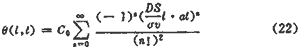
将式(22)代入式(17)得
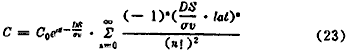
代入起始及边界条件(12)、(13)则可得
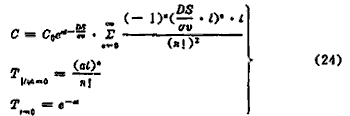
式(24)是接触氧化法过滤除铁的方程式。
方程式(24)当不考虑时间因素,则t=0时有
C=C0e-DS/σv·l (25)
亦可写成
ln=C0/C=DS/σv·l (26)
式(26)与天然锰砂过滤除铁方程式[1]具有相同的型式,说明公式[1]是本文导出的接触氧化法过滤除铁方程式的特例。
三、接触氧化法过滤除铁方程的验证
为了求解方程式(24),要预先求得系数D/σ和参数a。
接触氧化法过滤除铁要受到原水水质的影响,例如水中的H2SHSiO3-等也能被吸附在活性滤膜表面上,要占据活性滤膜表面的位置,相当于减少滤膜的表面积So,影响过滤除铁的效果。我们为了简化计算,固定So不变,而由系数D/σ来补偿。因此,系数D/σ因原水水质不同而有差异,需要由现场实验来确定。
用一清洁的成熟滤层,使之处于层流状态,进行实验,可以分别测得原水含铁浓度Co、出水含浓度C、滤粒当量粒径dcq、滤速v和滤层厚度l,它们遵循下列关系:
ln(C0/C)=D/σ·S0/v·l
式中 So=6(1-mo)Ψ/dcq
因此,实验点在C0/C和S0/v·l的半对数座标系中为一条直线,直线的斜率即为D/σ值。
图2为在佳木斯水质情况下测得的结果,当诸项因次分别采用:
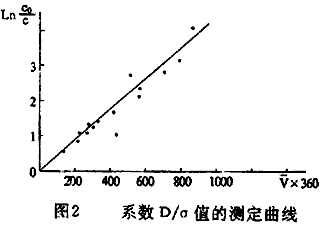
直径d[cm]、滤速u[m/hr]、含铁浓度C[mg/l]、滤层厚度[cm]时,可求出D/σ=1.12
a参数的物理意义可由下面推演给出,从方程式(6)
![]()
可以得到,滤层中所增加的除铁速率与滤层截留的铁质数量有增函数关系:
![]()
式中 Δu——由于滤层累积铁质的催化作用,保持出水含铁浓度不变时所能提高的滤速。
积分式(27)得:
a=[Δv(Co-C)/l]/ω (28)
亦可表达为
a=由滤层中截留铁质的作用所增加的去除铁量的速率/滤层中截留的铁量
所以参数a的物理意义是表示滤层中沉积铁质的除铁能力。参数a可由式(31)通过实验得出。一般,a=0.03~0.05。
我们采用含铁浓度14~20mg/l的地下水,按接触氧化法除铁处理,在不同条件下的理论计算值和实验值综合于表2中,可以看到计算值与实验值吻合得较好。
过滤除铁方程式表示为无究级数,计算很困难,表1中的理论计算值是用电子计算机计算的。为了便于手工计算,可以把其级数表示法复元为Bessel函数表示法:
![]()
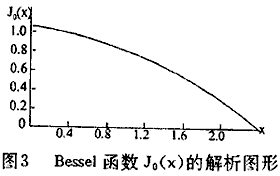
Bessel函数中的变量在正常情况下可以求得,且零阶Bessel函数存在如图3的关系。若令
4·DS/σU·l·al=X
计算出x后,由图3中查得x所对应的零阶Bessel函数值Jo(x),代入式(29)中,从而得到滤后水中的含铁浓度。
(m) 滤速(m/h) 时间(h) Co(mg/l) C理论(mg/l) C实验(mg/l)
2.0~2.5
0.70
10 10 17.4 2.09 2.40 36 17.4 0.76 0.6 30 8 19.1 10.1 10.8 20 19.1 10.3 9.6
0.30 20 10 16.3 13.6 11.0 50 10 18.9 14.5 15.4
1.6~2.0
0.70 25 15 18.7 7.98 6.2 10 30 17.8 1.52 0.7 1.0~1.25 0.77 10 20 21.4 0.45 0.1 40 6 14.3 4.06 3.8
以上,本文完成了曝气——接触氧化法过滤除铁的动力学基本微分议程的建立以及除铁滤层中含铁浓度分布规律数学模式的探求并且用实验对本文求出的数学模式进行了验证。
参考文献
[1]李圭白,《地下水除铁》中国建筑工业出版社1987
[2]高进雄,《水道协会杂志》第467号。
[3]戴镇生,“接触氧化除铁除锰机理及其在工程中的应用”《建筑技术通讯》1980,第2期
[4]上海化工学院,《基础化学工程(中册)》上海科技出版社,1980
[5]《数学手册》数学手册编写组,人民教育出版社,1978
[6]樊映川,《高等数学讲义(下册)》,人民教育出版社,1964。
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 [email protected] ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








