非稳定状态下活性污泥法处理系统最优控制的研究
出 自: 《中国给水排水》 1989年第1期第14页
发表时间: : 1989-1
彭永臻
(哈尔滨建筑工程学院)
摘要:本文以非稳定状态下的活性污泥法处理系统,作为最优控制的研究对象。根据现代控制理论,在有出水水质和状态变量等约束条件下,建立能求出使目标函数为最小的最优控制和数学模型。最后,对这个数字模型,用计算机进行数值计算并绘图,求解出在几种不同的约束条件下,最优控制变量的变化规律。
前言
本文以进水流量和进水底物浓度,随时间不断变化的非稳定状态,完全混合式活性污泥法处理系统(以下简称处理系统)作为控制对象;以处理系统的总运行费用为目标函数。分别按无约束条件下、有约束条件下的最优控制,来研究非稳定状态下的最优控制。
完全混合式活性污泥法处理系统的流程,如图1所示。
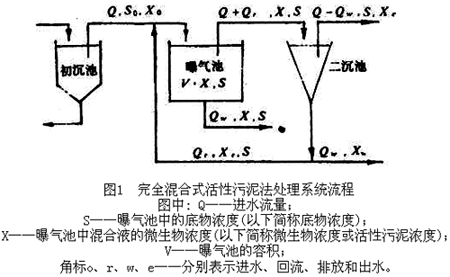
进水中微生物浓度X 0 和出水中微生物浓度X e 都非常低,并且是一进一出,因此,在进行物料衡算时可忽略不计。为了简化,假设进水的底物经初沉池后都是溶解性的,并且曝气池中的溶解氧浓度和二沉池中的活性污泥总量维持不变,这在控制中是可以做到的。如图1所示,有两种排放污泥的方式,即从污泥回流管线上排除或从曝气池中直接排除。有很多人认为:从曝气池中直接排放污泥更为合理,因为这种排泥方式有利于对系统进行更有效的控制及其后的污泥浓缩。因此,本文将根据从曝气池中排泥的流程,来推导处理系统的动力学模型和进行控制。
处理系统的控制变量有污泥的排放量Q w X,供氧量和回流污泥量Q r 、X r 。由于前面假定了曝气池中的溶解氧浓度和二沉池中的微生物总量不变,所以供氧量的控制,将由曝气池中的耗氧速度来决定。而回流污泥流量Q r 根据物料平衡可由下式来决定。

定义,从图1所示的特定的处理系统来看,无论是用污泥龄控制处理系统的运行,还是用BOD—污泥负荷来控制,最后都必须通过控制排放污泥量来实现。就是说,在假定了曝气池中溶解氧浓度和二沉池中的活性污泥总量不变的条件下,控制排放污泥量是过程控制的唯一手段,它和控制污泥龄或BOD—污泥负荷是等价的。
完全混合式曝气池中的底物浓度就是出水底物浓度,其浓度很低。因此其比底物去除速度和比微生物增长速度可分别用式(3)和式(4)表示。
q=KS(3)
u=Yq-K d (4)
式中:
q——比底物去除速度;
K——比底物去除速度常数;
u——比微生物增长速度;
Y——产率系数;
K d ——微生物的内源呼吸速率常数。
由于进水水质水量的变化,必然引起处理系统中状态变量和输出变量随时间的不断变化。因此,以时间为自变量,通过对图1所示的处理系统的微生物量和底物量的物料平衡,根据式(3)和式(4)建立状态方程,如式(5)和式(6)所示,这也是处理系统的基本微分方程式,建立系统的状态方程是解最优控制问题的必要条件。
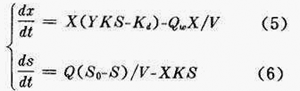
如果处理系统在较高的负荷下运行,表示比底物去除速度的公式(3)已经不能满足精确度的要求,这时应该采用式(7)。

由式(2)可见,回流污泥量Q r 是回流污泥浓度X r 、进水流量Q和微生物浓度X的函数。
回流污泥所需费用=(回流单位污泥量所需电费B)×(回流的污泥量)
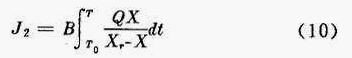
供氧所需要的费用,取决于溶解单位氧气的费用和曝气池中氧的消耗速度。氧的消耗速度R r 如式(11)所示:
R r =αQ(S 0 -S)十bVX =VX(αKS+1.42K d (11)
式中:
α——作为能量被去除的底物占总去除底物的比例,因此有α=1十Y;
b——微生物内源呼吸时的氧的利用速度,一般有b=1.42K d 。所以,
供氧所需费用=(溶解单位氧量所需费用C)×(耗氧量)
![]()
C的数值取决于供氧机械的效率和曝气扩散设备的效率。
排放出水中的污染物所需费用=(排放单位污染物所交付的费用或罚款w)×(排放的底物或污染物的量)

综合各式:

如果T 0 =0,T=1日,式(14)就表示处理系统每日所要支付的总费用。
为了求解出式(14)这个目标函数为最小的最优控制变量Q w (t),首先必须引入拉格朗日未定向量函数(称伴随变量)λ 1 (t),和λ 2 (t),以及哈密尔顿函数H(X,S,Q w ,λ 1 ,λ 2 ,t),如式(15)、式(16)和式(17)所示。满足H函数为最小值的最优控制,同时也使目标函数J取得最小值。
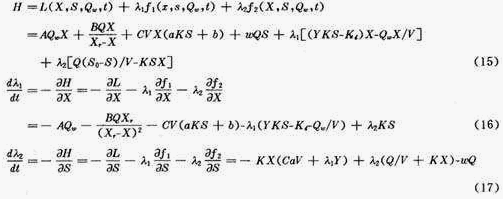
式中:f 1 和f 2 ——分别表示状态方程式(5)和式(6)的右边项。
根据控制论中庞特里亚金的最大值原理,以X,S,λ 1 ,λ 2 和Q w 为未知函数,由状态方程和式(15)~式(17)可组成最优控制数字模型的联立方程组,如式 (18)~式(22)所示,这个联立方程的解之一 ![]() 就是所要求的最优控制函数的解。状态变量的解X(t)和S(t)称为最优轨迹,是指最优控制下的状态变量。
就是所要求的最优控制函数的解。状态变量的解X(t)和S(t)称为最优轨迹,是指最优控制下的状态变量。
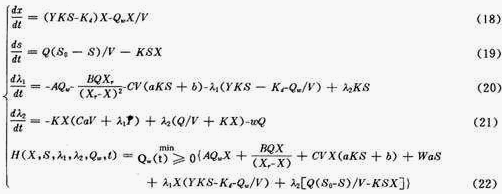
在联立方程式中共有五个方程(四个微分方程和一个代数方程),求五个未知函数Q w ,X,S,λ 1 ,λ 2 ,因此方程组有解。对于实际的污水处理系统来说,Q w (t)必须大于或等于零,Q w (t)≥0,也就是说在运行中只能从曝气池向外排放污泥,而不能往曝气池中投加活性污泥,所以式(22)必须写成如下的形式

这样,问题就转变成求控制变量在大于等于零[Q w (t)≥0]的范围内,目标函数的最小值和最优控制变量Q w (t)。这样的最优控制问题不能简单地用变分法来求解,而只能用庞特里亚金的最大值原理来解决。
二、有约束条件最优控制的数学模型
如果用平均出水质量达到排放标准,来约束处理系统的出水质量,同时约束处理系统每一个周期前后的状态变量基本相同,那么,本文所研究的最优控制,就变成了在满足某一出水质量和末端约束条件的基础上,求出使运行费用这一目标函数为最小的最优控制问题。
以处理系统的运行费用J作为目标函数,在非稳定状态下的某一期间(从T 0 到T),用泛函数表示,如式(23)所示。
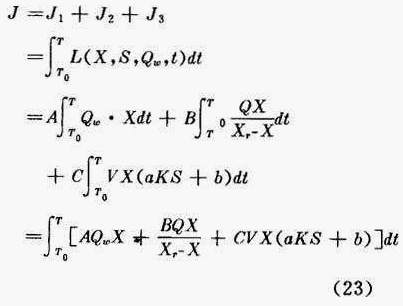
式中:J 1 ——污泥处置费;
J 2 ——回流污泥费用;
J 3 ——曝气费;
A——单位污泥量处置费(分/kg·污泥);
B——回流单位污泥量所需电费(分/m 3 );
C——溶解单位氧量所需电费(分/kg·O 2 );
α——作为能量被去除的底物,占总去除底物的比例,因此有α=1-Y;
b——微生物内源呼吸时氧的利用速度,
一般有b=1.42K d ·d 1 。如果T 0 =0,T=1日,式(23)就表示处理系统每日的运行费用。
使每日平均出水底物浓度 ![]() 小于或等于排放标准S st ,应满足式(24):
小于或等于排放标准S st ,应满足式(24):

若处理系统的末端状态受到下列m个条件的约束
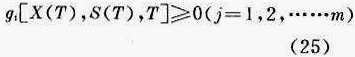
式中:T——末端的时刻,若以一日为周期,则T=1。
若在目标函数中加入另一形式的补偿函数,通过使新的目标函数〔如式(26)所示〕,为最小这个手段,来满足式(25)的约束条件,
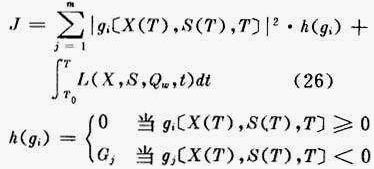
式中:G j ——相当大的正数,其值根据约束条件的精确度来确定。
从式(26)可见,当式(25)的约束条件都被满足的话,有h(g j )=0,式(26)的目标函数就变为单纯处理系统的运行费用;而当不满足约束条件式(25)时,有h(g j )=G j ,使式(26)的目标函数值增大,只有使该值趋近于最小值时,才能得到最优控制的解。那么,预先设定的G j 的值越大,式(25)的约束条件就越能得到满足,在 一定的误差范围内就可以得到满足式(25)中;所有的约束条件的最优控制函数。
为满足式(24)中平均出水底物浓度,低于排放标准这个约束条件,由状态变量Z(t)得:
![]()
令Z(T 0 )=0,得积分式:
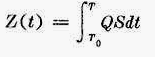
这样,式(24)中的积分型的约束条件,就可以变成末端状态型的约束条件
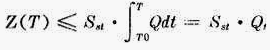
式中:Q t ——每日进水总流量。
可见,新的状态变量Z(t)的物理意义是在某一期间T 0 ~t内,处理系统所排放的底物数量。那么Z(T)就是每日(一周期)排放的底物总量。根据最优控制理论,由于增加了一个新的状态变量Z(t),状态方程和拉格朗日未定系数方程各增加一个。哈密尔顿函数如式(27):
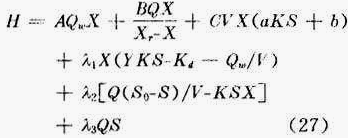
根据庞特里亚金的最大值原理,式(18)(19)是状态方程,其初始条件为已知,因为以日为一个控制周期,有T 0 -0状态变量的初始值,如下式所示:
X(T 0 )=X(0)
S(T 0 )=S(0)
Z(T 0 )=Z(0)=0
根据最优控制理论,它的初始条件未知,但末值条件由下式给出:
λ 1 (T)=-2G 1 [X(T 0 )-X(T)]
λ 2 (T)=-2G 2 [(ST 0 )-S(T)]
λ 3 (T)=-2G 3 [Q t ·S st -Z(T)]
由此可见式(18)—(22)联立方程组中,共有七个方程式和七个未知函数(X,S,Z,λ 1 ,λ 2 ,λ 3 和Q w ),其中有六个微分方程式并已知六个边界条件,联立方程可解。
为了举例说明最优控制在污水处理系统中的应用,求出方程式的解,首先假定动力学常数和其它系数的值,如表1所示。每日进水流量和进水底物浓度随时间的变化规律如式(28)和式(29)所示,假定回流污泥浓度X r 的变化如式(30)所示。
动力学常数及其它系数的假定值 表1
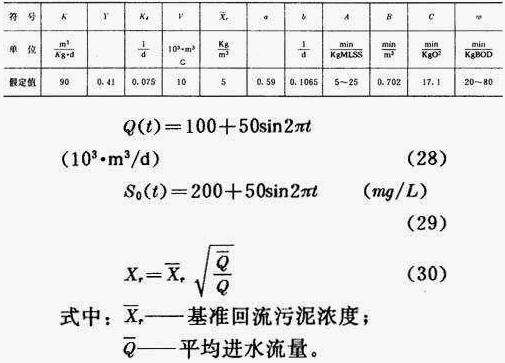
将式(28)~(30)和表1中的常数代入联立方程式(18)~(22),然后根据处理系统已知的初始条件,就可以求出数值解。因为污泥处置的费用与处理方式、污泥成分以及处理程度等很多因素有关,其处理所需要的费用相差很大,在表1中将单位污泥处置费A的取值,确定在5~25分/kg污泥之间。另外,在表1中将排放单位污染物BOD所需要的费用w的取值范围确定在20~80分/kgBOD之间。首先令A=5,w=80 代入联立方程后用计算机进行数值解析。得到的最优控制函数Q w (t)、状态变量的最优轨迹X(t)和S(t)随时间变化的情况,然后用计算机直接作图如图2(α)所示,处理系统所需要的总费用J和相对应的平均出水底物浓度 ![]() 随着数值计算次数N的增加向最优值逼进的情况如图2(b)所示。最后得到了最小的总费用Jmin=392.67(10 3 分/d=3926.7(元/d)。总费用为最小的情况下平均出水底物浓度(以下称最优平均出水底物浓度)
随着数值计算次数N的增加向最优值逼进的情况如图2(b)所示。最后得到了最小的总费用Jmin=392.67(10 3 分/d=3926.7(元/d)。总费用为最小的情况下平均出水底物浓度(以下称最优平均出水底物浓度) ![]() =15.22mg/L。这就是说,平均出水底物浓度
=15.22mg/L。这就是说,平均出水底物浓度 ![]() 高于或低于15.22mg/L其总费用J都将超过3926.7元/d。因为当
高于或低于15.22mg/L其总费用J都将超过3926.7元/d。因为当 ![]() >15.22mg/L,虽然能节省总费用中的运行费(J 1 ,J 2 ,J 3 ),但排放污染物所支付的费用J 4 却升高了;反之,当
>15.22mg/L,虽然能节省总费用中的运行费(J 1 ,J 2 ,J 3 ),但排放污染物所支付的费用J 4 却升高了;反之,当 ![]() >15.22mg/L时,J 4 的值虽然降低了,但运行费用肯定要增加。图2(α)所示的最优控制函数Q w (t)的变化形态近似于控制论中的开关控制(bang-bang控制)。
>15.22mg/L时,J 4 的值虽然降低了,但运行费用肯定要增加。图2(α)所示的最优控制函数Q w (t)的变化形态近似于控制论中的开关控制(bang-bang控制)。

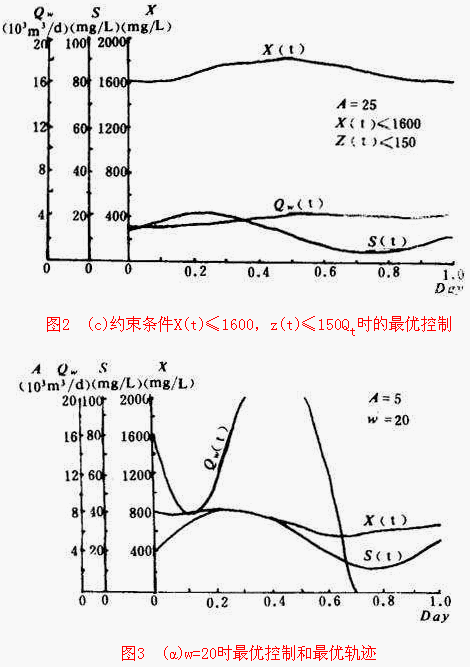
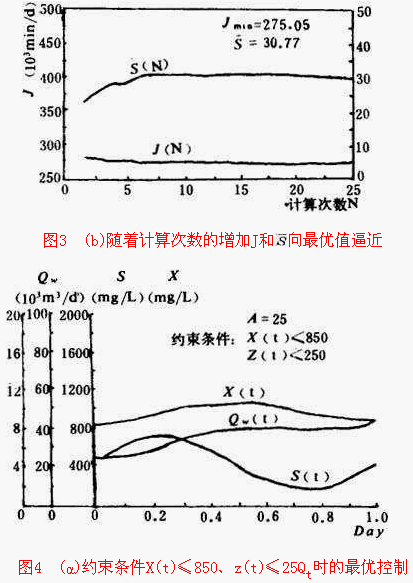
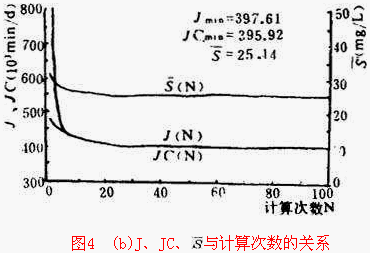
然后令w=50,w=35,w=20(分/kgBOD)其它条件不变,来分别求解联立方程,得到的最优控制Q w (t),最优轨迹X(t)和S(t),最小总费用J mi 以及最优平均出水底物浓度 ![]() ,如图3所示。带有约束条件的计算结果如图2(c)。图4表示出水排放标准为25mg/L时,相应的最优控制计算结果。可以看到,排放标准的约束条件以及使末端状态变量和初期状态变量相同的约束条件,都基本能得到满足。因为它在满足一些约束条件的基础上,使人们最关心的目标函数为最优。几乎所有的城市污水和工业废水的流量、浓度,都是随时间不断变化的,有时其变化速度和幅度很大,这给处理系统的运行管理带来很多麻烦。如果能采用最优控制,不仅能定量地控制出水质量,还能尽量减小运行费用。
,如图3所示。带有约束条件的计算结果如图2(c)。图4表示出水排放标准为25mg/L时,相应的最优控制计算结果。可以看到,排放标准的约束条件以及使末端状态变量和初期状态变量相同的约束条件,都基本能得到满足。因为它在满足一些约束条件的基础上,使人们最关心的目标函数为最优。几乎所有的城市污水和工业废水的流量、浓度,都是随时间不断变化的,有时其变化速度和幅度很大,这给处理系统的运行管理带来很多麻烦。如果能采用最优控制,不仅能定量地控制出水质量,还能尽量减小运行费用。
本文认为,虽然最优控制的实施有待于活性污泥法动力学模型的完善和处理系统计算机自动控制的进一步开发。但是在设计污水处理厂时,以污水厂的建设费为目标函数的、静的最优化和以运行费用为目标函数的、动态的最优控制相结合,来进行研究,将会使这方面的研究更加完善,这应该是今后的研究课题。
主要参考文献
[1]Fan. L. T,et al; "Dynamic Analysis and optimal Feedback Control Synthesis Applies to Biological Waste Treatment "Jour.Water Res. 7.1609(1973)
[2]Angelbeck, D. I. , and Shah Alam, A. B. ,"Simulation Studies on Optimization of the Activated Sludge Process,", Jour.WPCF. ,50 31-39(1978)
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 [email protected] ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








