大口径水管的测流研究

出　　自：《中国给水排水》 1987年第6期第19页
发表时间：1987-6

许建华

( 同济大学 )

摘要：本文根据理论分析和通过对不同雷诺数情况下测得的大量数据组的计算，提出一种适用于任何雷诺数情况下的新的大口径水管测流方法。

大口径水管流量如何准确测定，是当前给水事业中普遍存在的一个重要问题。由于水管横断面上各点流速的大小相对关系随雷诺数Re 等不同而变异甚大，故国内外目前应用的电磁流量计、超声波流量计、文丘利流量计、插入式涡轮流量计和均速管流量计等大口径水管测流设备，均不同程度地存在测量精度不够理想和能耗较大等缺陷。
对于管内水流为层流流态的长直管段，管道横断面流速分布呈抛物线规律，管轴处流速U0 最大。在管道半径R方向上距离管轴心为Ri 处的流速Ui 为:

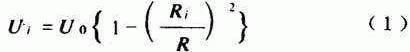
管轴心流速U 0 是断面平均流速 的二倍，即 。圆管中相当于断面平均流速 的点，出现在离管轴R i =0.707R处，也即相当于离管壁0.147D处。
在实际应用中，管内水流一般均为紊流流态。紊动的水流质点在沿前进方向运动的同时，兼有垂直于前进方向的横向分速。水流质点的紊动导致动量交换、使管轴附近各点流速比层流时的分布大大平均化。脉动状态的紊流流速可用各点的时均流速表达，长直管段管道横断面上各点的时均流速U i 一般呈指数曲线规律分布:

式(2)中，n值随圆管雷诺数Re变化，一般n=7~10。因之，紊流流态下不同的Re值时的管道断面平均流速 与管轴处最大流速U 0 比值k在较大幅度范围变化(有资料介绍: 也就不易通过测定管轴流速U 0 来准确计算 及管道流量Q。
为了能方便准确地测定大口径水管的流量，应设法寻找圆管横断面上基本不随雷诺数大小变化的、 基本稳定的时均流速为U n 的部位，以便在任何雷诺数时都可通过测定该部位的时均流速U n 值，进而求得断面平均流速 和管道流量Q。
一、圆管紊流流速分布规律的理论探讨

根据L.Prandtl对紊流流态下圆管管流情况所作的假定，推导得圆管断面各点流速U i 的理论公式为:

式中: λ——圆管沿程阻力系数。
从式(3)可推算得圆管的平均流速 应发生在离管轴R i =0.777R处也就是发生在离管壁0.112D处。
若按本文公式(2)，并以n=7~10代入，则可推算得圆管的平均流速 应发生在离管轴R i =0.758R~0.763R处，也就是发生在离管壁0·121D~0.119 D处。

二、圆管紊流流速分布实测资料的分析研究

我们曾按照将圆管断面划分为5个等面环的方法，用毕托管分别实测了某冷却塔Dg700mm 进水钢管和某水厂Dg400mm原水铸铁管段的不同流量和雷诺数情况下的四十二组工况的各等面环测点毕托管压差值h i ，由于篇幅所限见表1 A及表1B列出二十组工况点的具体数据。Dg700mm钢管的实测内径D=685mm，Dg400 mm铸铁管的实测内径D=390mm。限于现场条件，该二管段被测断面的上游直管段长度大于管径的8倍，下游直管段长度大于管径的5倍，基本保证了被测断面的水流分布不受上游弯头和下游闸阀等干扰影响。每个测定工况均以各等面环的中心点为测点，各测点距圆管轴的距离R n 按下式计算确定:

式中: m——圆管断面划分的等面环数量；
n——该测点所在的等面环号次。由之算得从管壁开孔处插入毕托管向管内伸入的各测点离孔壁距离依次为:1——0.026D,2——0.082D，3——0.146D，4——0.226D，5——0.342D，6——0.658D，7——0.774D，8——0.854D，9——0.918D，10——0.974D。测得各工况测点的毕托管压差值h 1 ，h 2 ，……h 10 和管轴点的毕托管压差值h 0 ,计算了测点1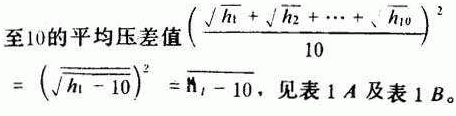

表中各工况测点数据均系一次测读所得。该二管段的实试工作中，对Dg700mm钢管使用的是普朗特毕托管，对Dg400mm铸铁管使用的是双脚毕托管。该二毕托管所接U形水柱差压计的工作液均使用清水。
Dg700mm管各测点毕托管压差 值 表1A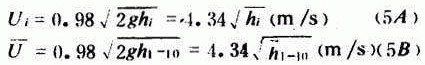

Dg700mm管道测流所用的普朗特毕托管校正系数c=0.98，测得的各点压差h i 可按下式换算成流速: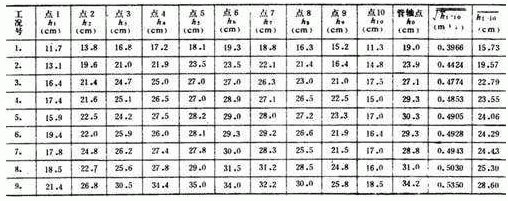

Dg400mm管道测流所用的双脚毕托管的两根管内的液柱高差为h=1.43U 2 /2g,各点压差可按下式换算成流速:

Dg700mm管和Dg400mm管各工况的过水流量分别为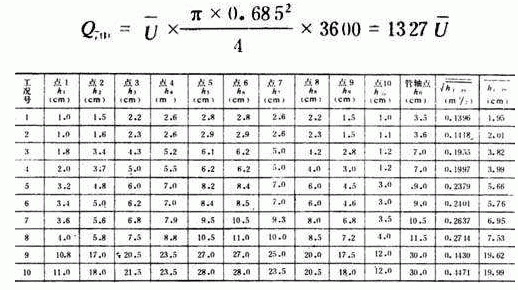

Dg400mm管各测点双脚毕托管压差 值 表1B

二条管道各工况管轴测点的毕托管压差和流速分别为h 0 和U 0 ，可按下式算得每一工况的管道断面平均流速 与管轴点流速U 0 的比值k:

为了对应了解不同工况时，圆管雷诺数Re 与反映管道断面流速分布情况的K值的关系，按下式计算各管道不同水流工况的Re值:

式中: γ——大气压下，不同温度时水的运动粘度(c m 2 /s)
表1 A和表1 B各工况毕托管压差资料，是在下述水温条件下测得的:
Dg700mm:水温35℃左右，γ 35C =0.72×10 2(m 3 /s)
Dg400mm:水温20 C左右，γ 20C =1.0×10 2(m 3 /S)于是，该二管各工况的雷诺数可分别按下列二式计算:Dg700m m:

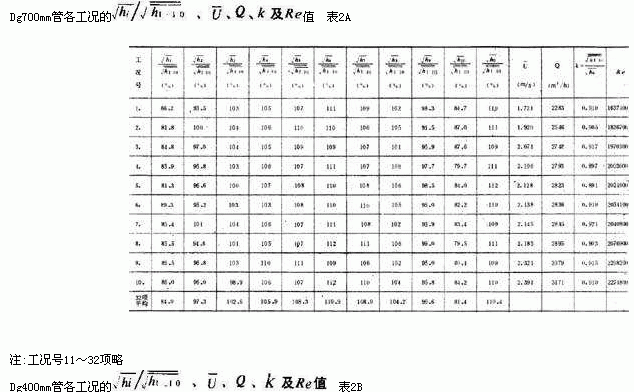
Re值，分别计算汇列于表2 A和表2 B中。从表2 A和表2 B可以看出:该二条直管段所测的四十二个工况所跨越的平均流速 和雷诺数Re 的幅域很广 ， 0.517~1.654m/s，Re=201，630~645，060)、工程实际常用的流速一般均已涉及，因此测试资料有较好的代表意义，并可从中探求圆管流速分布规律。

绘制出管道断面层流流速分布曲线I和Dg400 mm素流流速分布曲线Ⅱ、Dg700mm紊流流速


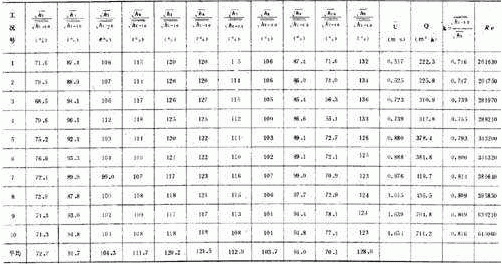
分布曲线Ⅲ，汇总绘制成图。


图中，纵坐标 处引出的水平虚线与曲线1、Ⅱ、Ⅲ相交点，即为层流与紊流流态下出现平均流速 的所在部位。如前所述，层流流态时平均流速出现在离管壁0.147D 处。紊流流态时，Dg400mm圆管和Dg700 m m 圆管的平均流速分别出现在离管壁0.125D和0.11 D处，与前面用理论公式(3)或公式(2)分别推算得出的离圆管管壁0.112 D处或0.121 D~0.119D的范围基本吻合。从图可见，当雷诺数Re较小时，上述区间的断面流速分布曲线斜率较大，若相当于 值的测点选位不当，该点时均流速测定值仍可能与 值有不大于5%的误差。
从图可见，管流雷诺数Re越大，紊流越剧烈时，水流质点激烈紊动导致管轴附近纵问速差越来越小，K值随Re值增大而渐减少。图显示了曲线I、Ⅱ和Ⅲ在管轴二侧均基本上相交在距管壁0.15D附近，也就是说，不论圆管内水流Re在什么范围，距管壁0.5 D处的时均流速U 0.15 D与平均流速 之比值基本稳定，从图可见0.15D处的 ，因此，可用毕托管伸入管内测定距孔壁0.15D处的时均流速U 0.15D 并以下式求得断面平均流速 :

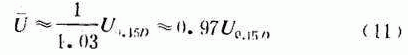
这将是一种简便有效、能适用于任何Re值和U情况下的大口径水管流量测定方法，精度较高，且测流水头损失较小。

参考文献

[1] 周善生:《水力学》，(1981)
[2] 周亨达:《工程流体力学》，(1983)
[3] [日]川田裕郎、小宫勤一、山崎弘郎:《流量测量手册》，计量出版社，(1982)。
[4] L，Prandtl.O.G.Tietjens:Applied Hydro and Aero mechanics
[5] A.C.Wal shaw.D.A.Jobsoi:Mechanics of Fl uids (Third Editon).1979