穿孔管配水系统均匀布水问题研究
| 论文类型 | 技术与工程 | 发表日期 | 1986-01-01 |
| 来源 | 《中国给水排水》1986年第1期 | ||
| 作者 | 王绍文,刘灿生 | ||
| 摘要 | 本文详细研究了穿孔管配水系统水力特性,提出了管内压头计算公式及诺模图,试验证明理论公式与试验结果基本相符;并提出按管内压头来改变开孔面积的布孔方法,以便保证用于低水头滤池时布水的均匀性。 | ||
出 自: 《中国给水排水》 1986年第1期第36页
发表时间: 1986-1
王绍文;刘灿生
( 哈尔滨建筑工程学院)
摘要:本文详细研究了穿孔管配水系统水力特性,提出了管内压头计算公式及诺模图,试验证明理论公式与试验结果基本相符;并提出按管内压头来改变开孔面积的布孔方法,以便保证用于低水头滤池时布水的均匀性。
目前低水头滤池均采用小阻力配水系统,这种系统配水不均匀,反冲洗效果差。本文把穿孔管配水系统用于低水头滤池上,并对穿孔管系统的水力特性进行了研究,提出根据管内压头变化来改变开孔面积的方法,以保证低水头时反冲洗布水的均匀性。
一、管内压头计算
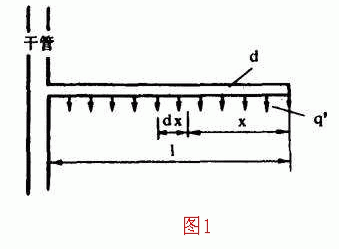
取长为1、管径为d的支管,将其抽象成每个单位长度上泄出q′流量的连续泄水管。以支管末端为坐标原点,在x与x+dx断面处列伯努里方程式 [1]

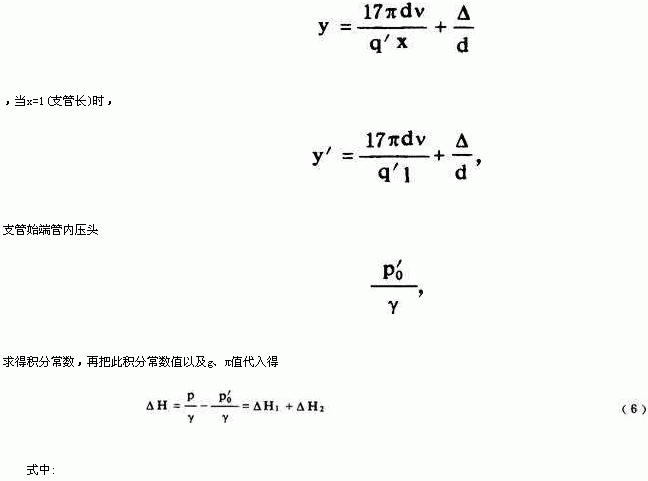
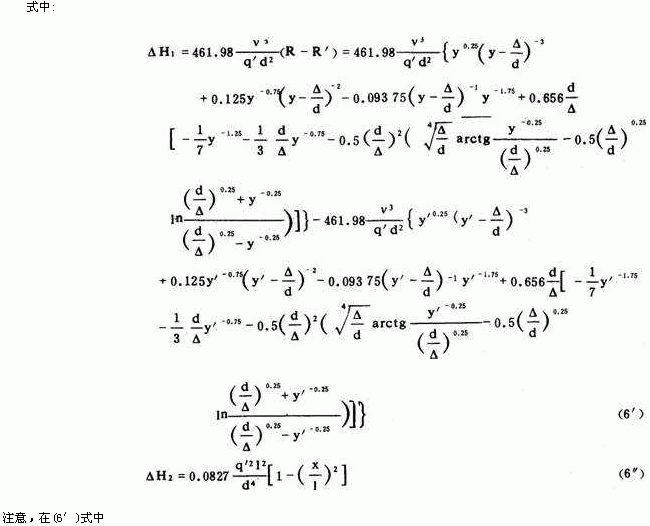
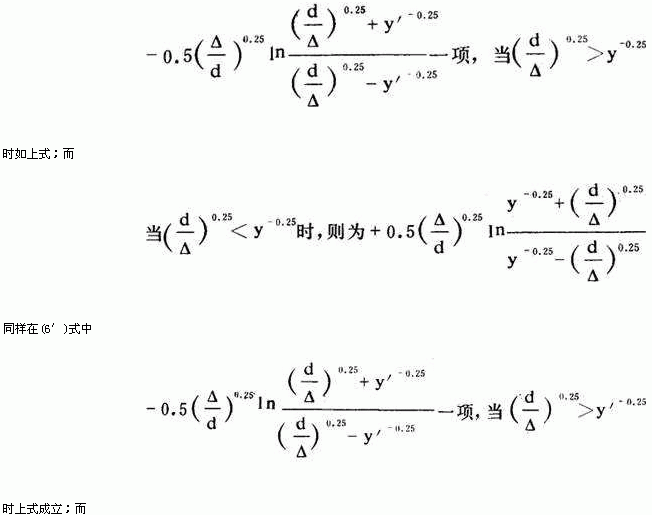
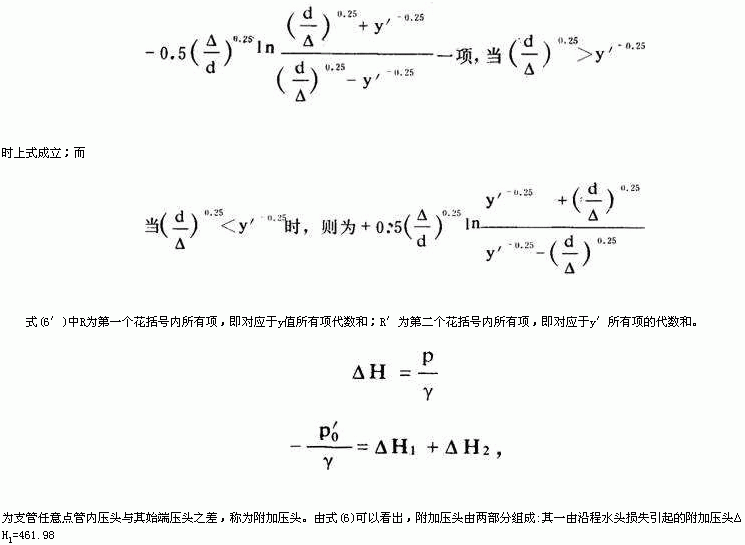

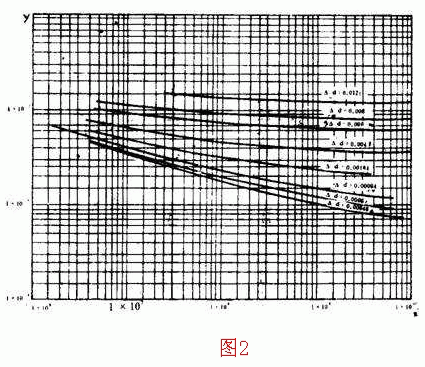
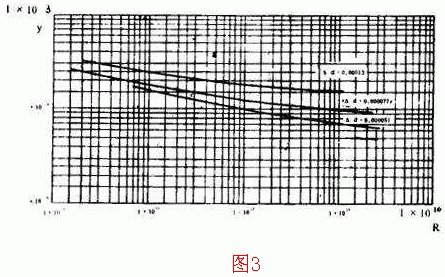
为了简化式(6)的计算,图2、3给出计算R与R′的诺模图。已知y及y′值可由图中求得其所对应的R及R′值。在计算支管任意点附加压头时,分别算出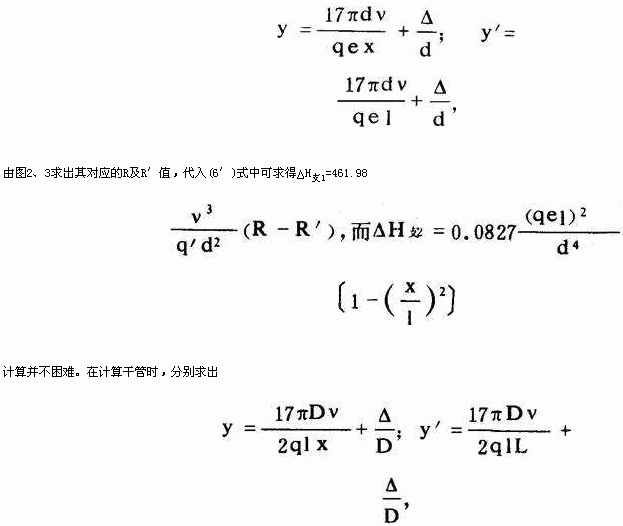
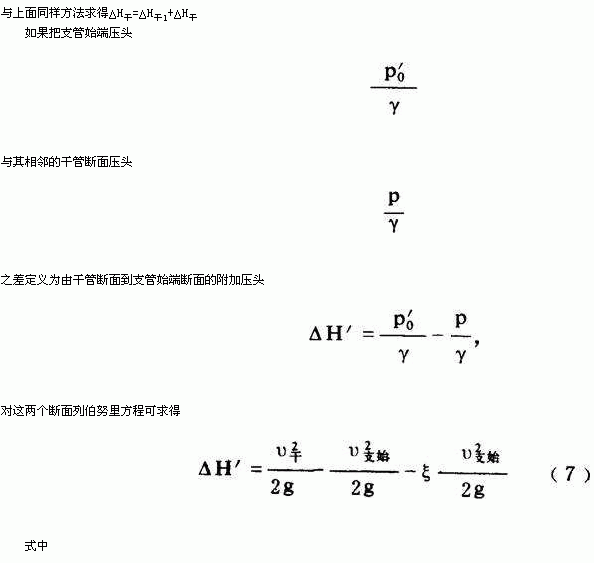

两项可以抵消,因为ξ 1 接近1。由此可知ΔH′与两个因素υ 支始 、ξ 2 有关;而ξ 2 取决于支、干管直径比d/D,当滤池规格变化时,d/D变化不大,ξ 2 变化可以忽略,故ΔH′只与υ 支始 有关。T型三通连接时,ΔH′可直接按图4查取。
显然,管路系统中支管任意点的附加压头ΔH=ΔH 支 +ΔH 干 +ΔH′。而支管任意点内压头为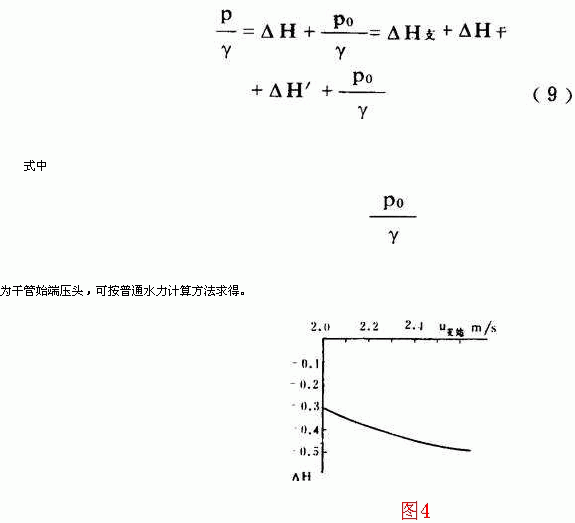
二、实验与分析
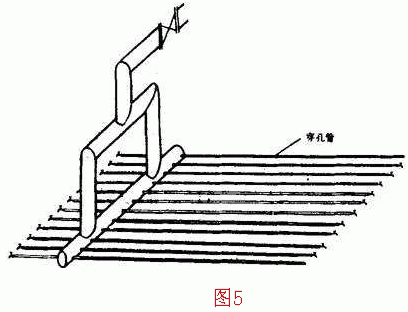
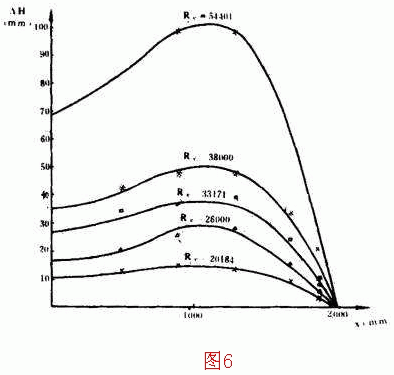
为了验证附加压头的计算公式和穿孔管系统的水力特性,试验设备如图5所示。外侧两根长支管为穿孔管,其它均为装有阀门的普通钢管。长支管上均装有测压孔,穿孔管是等间距布孔,孔距85mm,孔径5 mm。试验时流量用普通体积法测量,穿孔管糙粒高度Δ,是根据不同流量下,由穿孔管各测压孔测得的附加压头,用(6)式通过微型电脑PC—1500反标出来。图6绘出穿孔管入口各不同雷诺数时,各测压孔处附加压头的试验数值以及按(6)式算得曲线。由图6可看出理论计算与试验结果基本吻合。
实际上,穿孔管入口段是水流由于管进入支管局部阻力影响区。在这一区域中,压头分布要受到影响,只有超出影响长度之后,其分布规律才稳定。由图6可看出,即使是在入口局部阻力影响区内,试验点也与(6)式基本吻合。这说明入口局部阻力在入口段所造成的压头差,与由孔口均匀泄流所造成的压头差相比,是很小的,可忽略。由此可得出结论:(6)式不仅可用于穿孔管的稳定段,也可用于其入口段。
上述干管进入支管局部水头损失计算方法,没有考虑入口局部阻力之间的相互影响,显然是有误差的。为了研究这一计算误差对配水均匀性的影响,而进行了总体试验。把6根长支管的流量均调到相同时,来观察各支管各相应测压管读数。表1列出一种工况下各支管流量及相应的各测压孔读数。由表1可以看出,当各支管流量基本相同时,其相应部位测压管读数也都基本相同,其它工况下也得到同样的结果。所以我们可认为,对于对称布置的穿孔管系统,支管入口局部阻力计算误差对各支管都是基本相同的。
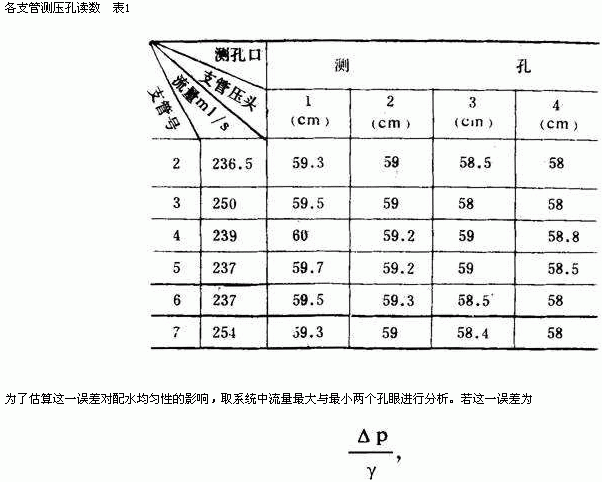




,即支管入口局部损失最大的计算误差,使流量产生的相对误差不足于2.8%。据此,我们可得出结论,尽管计算支管入口损失有误差,但不影响配水均匀性。
三、穿孔管配水系统均匀布水计算
从支管孔口流出的水流速度取决于支管内外压头差
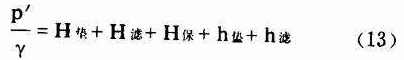
反冲洗时管外压头可按下式算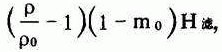
式中:H 垫 为垫层高度;H 滤 为滤层厚度;H 保 为滤层表面至排水槽水面高度;h 垫 +h 滤 为垫层和滤层的水头损失。而h 垫 =0.022qH 垫 ;h 滤 =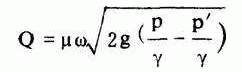
式中ρ为滤砂比重(石英砂ρ=2.65,锰砂ρ=3.2);ρ 0 为水的比重;m 0 为滤层反冲洗时的孔隙度,一般可取m 0 =0.42~0.45。
通过孔眼流出流量可按流量系数μ取决于孔口阻力系数ξ 0 。由于孔眼很小,其雷诺数很低,所以很难达到阻力平方区,故ξ 0 (也即μ)是随流出孔眼雷诺数而变化,耶哥洛夫所进行的试验证明 [5] ,孔口流量系数μ主要取决两个因素:其一是构造条件,可用管壁厚度δ与孔口直径d 0 之比δ′=δ/d 0 .来反映;其二是流动状态,可用管道中雷诺数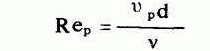
和孔口雷诺数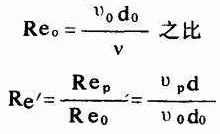
来反映。耶哥洛夫把试验结果整理成经验公式![]()
对于滤池穿孔管系统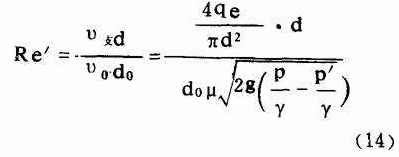
显然(14)式等号右端的μ依赖于Re′。所以用耶哥洛夫经验公式,不能直接求得Re′与μ的值,必须进行试算。为了便于计算,把耶氏经验公式改造为图7 [2] ,同时在图上给出μRe′=a,(a等于各数值的等值曲线)。由(14).式可以看出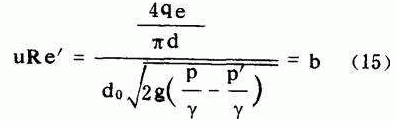
由(15)式可求出b值。在图7上根据μRe′=b与δ′=δ/d 0 的数值直接求得各孔眼流量系数μ值。
为了便于计算,把上面讨论归纳成以下计算步骤。
第一步把整个滤池分成N个相等的分区。每个分区取中间一根支管做为计算支管,再把这根计算支管分成长度相等的n段,取每段中点做为计算点,这样就有Nn个计算点。显然N、n数值取得越大,计算越精确,工作量越大。
第二步按(6)、(9)等式与图2、3计算每个计算点的管内压头。
第三步按式(15)及图7计算每个计算点的孔口流量系数μ值。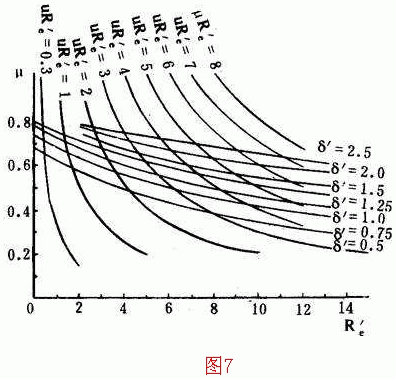
第四步按(13)式计算穿孔管管外压头![]()
第五步计算每根计算支管的各区段所需孔口面积和孔口数目。每一个区段所需孔口面积可按下式计算,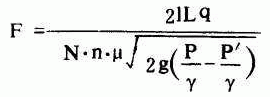
每个区段所需孔口数目m可按下式计算m=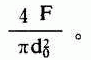
在滤池同一分区其它支管都按计算支管同样布孔。
结束语
本文提出计算管内压头的公式与诺模图不仅可用于穿孔管的稳定段,也可用于入口段。本文提出的计算由干管到支管入口局部水头损损的方法是有误差的,但不会对布水均匀性产生影响。按管内压头来改变开孔面积的布孔方法,能保证穿孔管系统低反冲洗水头时布水的均匀性,而且不会对滤池集水均匀性产生影响。
参考文献
1. 王绍文、刘灿生“穿孔管配水系统均匀布水水力计算“哈尔滨建工学院学报1984年第3期。
2. 王绍文、刘灿生“穿孔管配水系统均匀布水水力计算”(续)哈尔滨建工学院学报1984年第3期。
3. 成都科技大学水力学教研室编“水力学”人民教育出版社
4. 周漠仁主编“流体力学泵与风机”建工出版社
5. ЕГОРОВ “Гидравлнчсскнй Расчг Трубчагыхснсгсм для Распределения В оды В Водопрово дныхО чсисгых Сооружениях”1960.
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 [email protected] ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








